GLMMでWAICを計算するときの困難

glmmstanを作ってから，MCMCで分析するのが楽しくて楽しくて仕方がない清水です。

で，glmmstanでWAICも計算できるのですが，どうもわからないことが出てきました。で，いろいろ考えた結果，「わからん」ということで，そのわからなさについてまとめます。

WAICについて

WAICはWidly-Applicable Information Criterionの略で，AICのもついくつかの前提条件をゆるめて利用できる新しい情報量規準です。僕はぶっちゃけ数理的なところはさっぱりわかりませんが，WAICを作った渡辺先生のWebサイトを見るに，AICには

AICは事後分布が正規分布で近似できる場合のみ使える
AICはモデルに真の分布を含んでいる場合のみ使える
AICはサンプルサイズがとても大きいことを仮定している

ということらしいです。逆にWAICはこの条件が満たされてなくても使えます。逆に，これらの条件が満たされれば，AICとWAICは（確率的に）一致するそうです。

で，GLMMはおそらく上の条件を大抵満たすのだろうと思います。少なくとも最尤法がまともな推定をする範囲に限定すれば，AICはGLMMに対しても有効に機能するでしょう。

ただ，データがどういう確率分布に従って発生しているのかを判断したい場合は，２．の制約により使えない，らしいです。モデルが真の分布を含んでいる必要がある以上，分布を超えてどのモデルがいいかを比較することはできないからです。

なら，GLMMでもWAICを使えると便利かなーと思ってglmmstanを作ってみたわけです。

AICとWAICを比較してみよう

というわけで，AICとWAICを比較して，挙動を見てみようと思ったわけです。

SapporoRでも使った，2014年のプロ野球野手（規定打席が1/3以上の選手141人）のホームラン数のデータを使ってみます。なお，データはプロ野球Freakから手にはりいます。

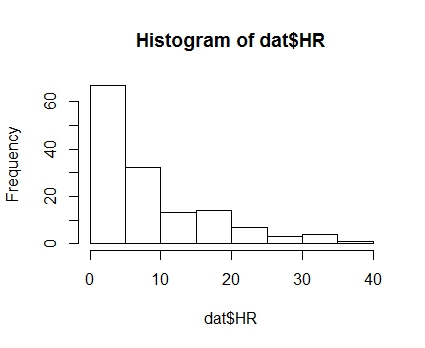
まずはホームラン数のヒストグラムを見てみましょう。

dat <- read.csv("baseball.csv")
hist(dat$HR)

1 2	dat <- read.csv("baseball.csv") hist(dat$HR)

このように，ポアソン・・・ではないような離散分布となります。

ここで無茶を承知でポアソン分布に近似させてみましょう。まずはglm()で最尤法による推定を行います。サンプルサイズは小さいですが，まぁそんな複雑なモデルではないし，なんとかなるでしょう。

result1 <- glm(HR~1,dat,family="poisson")
AIC(result1)

1 2	result1 <- glm(HR~1,dat,family="poisson") AIC(result1)

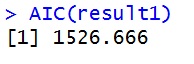
というわけで，AIC=1526となりました。次に，stanを使ってWAICを計算してみます。stanコードは以下です。

data{
  int<lower=1> N;
  int<lower=0> HR[N];
} 
parameters{
  real beta;
} 
model{
  beta ~ normal(0,1000);
  HR ~ poisson(exp(beta));
} 
generated quantities{
  real log_lik[N];
  for(n in 1:N){
    log_lik[n] <- poisson_log(HR[n], exp(beta));
  }
}

data{

int N;

int HR[N];

}

parameters{

real beta;

}

model{

beta ~ normal(0,1000);

HR ~ poisson(exp(beta));

}

generated quantities{

real log_lik[N];

for(n in 1:N){

log_lik[n] <- poisson_log(HR[n], exp(beta));

}

これをcode1にいれて，以下のコードでstanをRで走らせます。

datastan1 <- list(N=length(dat$HR),HR=dat$HR)
fit1 <- stan(model_code=code1,data = datastan1,iter=2000,chains=2)
#WAIC
loglik <- rstan::extract(fit1,"log_lik")$log_lik
lppd <- sum(log(colMeans(exp(loglik))))
p_waic <- sum(apply(loglik,2,var))
waic <- -2*lppd + 2*p_waic
waic

datastan1 <- list(N=length(dat$HR),HR=dat$HR)

fit1 <- stan(model_code=code1,data = datastan1,iter=2000,chains=2)

#WAIC

loglik <- rstan::extract(fit1,"log_lik")$log_lik

lppd <- sum(log(colMeans(exp(loglik))))

p_waic <- sum(apply(loglik,2,var))

waic <- -2*lppd + 2*p_waic

waic

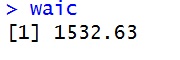
このように，WAICは1532となり，AICとまぁ，だいたい同じような値になりました。なお，このWAICは渡辺先生の論文の定義に2*Nをかけたものです。

個人差をGLMMでモデリングする

さすがに141人みんながおなじポアソン分布に従う，というのは無茶でしょう。打力には当然個人差があって，そこを考慮に入れないと全然予測が上手く行きません。

本来は打席数をオフセット項にいれて・・・とかするといいんですが，今回はそこはすっ飛ばしていきなり個人差をGLMMで検討してみます。

まずは最尤法で検討します。lme4パッケージのglmer（）で推定してみました。

result2 <- glmer(HR~1+(1|player),dat,family="poisson")
AIC(result2)

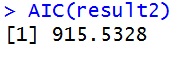
1 2	result2 <- glmer(HR~1+(1\|player),dat,family="poisson") AIC(result2)

glmerはラプラス近似だからあやしい！という人のために一応SASでガウスエルミート求積法による推定をしみてたらAICは915.45でまぁほぼ一致してました。

続いて，stanでWAICを計算してみます。stanコードは以下のようになります。rは各選手の変量効果で，それがさらに平均0の標準偏差tauの正規分布に従うと仮定します。

data{
  int<lower=1> N;
  int<lower=0> HR[N];
} 
parameters{
  real beta;
  real<lower=0> tau;
  real r[N];
} 
model{
  beta ~ normal(0,1000);
  r ~ normal(0,tau);
  for(n in 1:N)
    HR[n] ~ poisson(exp(beta+r[n]));
} 
generated quantities{
  real log_lik[N];
  for(n in 1:N){
    log_lik[n] <- poisson_log(HR[n], exp(beta+r[n]));
  }
}

data{

int N;

int HR[N];

}

parameters{

real beta;

real tau;

real r[N];

}

model{

beta ~ normal(0,1000);

r ~ normal(0,tau);

for(n in 1:N)

HR[n] ~ poisson(exp(beta+r[n]));

}

generated quantities{

real log_lik[N];

for(n in 1:N){

log_lik[n] <- poisson_log(HR[n], exp(beta+r[n]));

}

これをcode2にいれて，次のRコードを走らせます。

datastan2 <- list(N=length(dat$HR),HR=dat$HR)
fit2 <- stan(model_code=code2,data = datastan2,iter=2000,chains=2)

loglik <- rstan::extract(fit2,"log_lik")$log_lik
lppd <- sum(log(colMeans(exp(loglik))))
p_waic <- sum(apply(loglik,2,var))
waic <- -2*lppd + 2*p_waic
waic

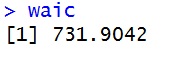
datastan2 <- list(N=length(dat$HR),HR=dat$HR)

fit2 <- stan(model_code=code2,data = datastan2,iter=2000,chains=2)

loglik <- rstan::extract(fit2,"log_lik")$log_lik

lppd <- sum(log(colMeans(exp(loglik))))

p_waic <- sum(apply(loglik,2,var))

waic <- -2*lppd + 2*p_waic

waic

・・・あれ？AIC（915）と全然違う・・・

何が違ったのか

というわけで，GLMMだとAICとWAICは結果が違ってきます。それがよくわからなかったのですが，以下，素人なりの考察です。

他にもいろいろなデータ，モデルで試してみましたが，変量効果が入っていない普通のGLMだとAICとWAICはほぼ一致します。なのでWAICを計算するコードが間違えてる，ということではないと思います。統計の専門家に聞いてみたところ，階層ベイズの場合であっても，WAICを推定するのはこれであっているようです。

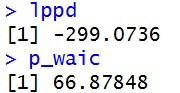
それでふんふん考えてたんですが，WAICの実効パラメータ数を表すp_wiacの値がとても大きいことに気づきました。

lppd
p_waic

1 2	lppd p_waic

66？でかくない？

ついでに，最初のポアソン分布を素直に当てはめたモデルだと，p_wiac=7.12でした。lppdは-759.19です。p_waicは対数予測分布の分散の和で計算されるので，予測分布の計算で用いられるパラメータの散らばりが影響します。なのでGLMだとサンプルサイズが十分大きければ，p_waicはパラメータ数に近くなるようです（データを触った感じで。数学的にはわかんない）。

このことから，変量効果をrで個別に推定しているので，それが実効パラメータ数として計算されてるんじゃないかと思ったわけです。つまり，個別の変量効果の値が，それぞれ推定されたパラメータとして扱われている，ということです。事実，予測分布の計算にrが含まれています。

これをもう少し具体的に言えば，各選手のホームランを打つ力がそれぞれ個別に推定されていて，その場合の予測誤差がWAICとして計算されているというわけです。

それがどうした，と思われるかもしれません。野球選手の場合は次の年もまぁだいたい同じ選手が活躍するので，ホームラン数の分布を予測するのにそれらのパラメータは利用できます。

しかし，社会科学で得るデータのほとんどは同じ人，同じ集団に対してサンプリングしません。よって，推定したい（というか予測に役立つ）パラメータは固定効果であるbetaと変量効果の分散性分であるtauだけです。

AICはパラメータ数はこの2つしか用いていないことになっているので，罰則としてAICに2☓2=4だけが－2対数尤度に足されています。実際，SASの結果を見ると-2対数尤度は910.45で，AICは914.45となっていて，4だけが足されています。個々の変量効果は推定対象になっていないのです。

これがAICとWAICが一致しない理由かな，と思います。

で，この方法で計算されるWAICはモデルの予測力を知るのに使いにくいなーと思うわけです。だって，個人差や個体差をそれぞれ推定しても，それらは次のデータを取るときには全く使えないことがほとんどだからです。それでAICよりもよい値が出ていても，ぶっちゃけ意味がありません。

じゃあどうしよう

ということですが，まだ僕はどうすればいいのかよくわかっていません。stanコードでどうやってrを直接推定せずに，tauだけを推定できるのかがわかりません。

なので謎は謎のままなのですが，とりあえずこの記事の考察をまとめておくことも悪くはなかろうと思って書いた次第です。

以上の考察がそもそも見当違いの可能性，かなりあります。もしかしたらstanで簡単に書けることを僕がうんうん悩んでたのかもしれません。そうだったらむしろうれしいので，ぜひご指摘ください。

ではー