今書いてる論文で使ったモデルなので、備忘録的に記録しておきます。そうしないと次やるとき絶対忘れてるので。
Actor-Partner Interdependence Model(APIM)は簡単に言えば、ペアデータの相互影響プロセスを分析する方法です。恋愛・夫婦・友人ペアとか、二者間会話データとか、双子とか、そんなのに使えます。
なお、以下の内容は
Olsen & Kenney (2006) Structural Equation Modeling With Interchangeable Dyads, Psychological Methods, 11, 127–141.に詳細が書いてあります。
日本語では、豊田秀樹編 2009 共分散構造分析(実践編) p81~92がわかりやすいです。
APIMとは
さて、Actor-Partner Interdependence Model(APIM)とは、Kenney(1996)で提案された、二者関係データ(Dyadic data)における相互影響プロセスを分析する方法論です。APIMでは、変数間の関連についてActor effectとPartner effectの二つを推定します。
例えば、ここで二者間会話のデータがあったとします。変数は発話量と会話満足感だとしましょう。このとき、会話における発話量が会話の満足感に与える影響を検討したいとします。すると、Actor effectは自分の発話量が満足感に与える効果を示し、Partner effectは相手の発話量が満足感に与える効果を示します。つまり、二者関係データを使って相互依存的な二人の個人内・個人間の影響関係を見ようとする方法なわけです。
ペアが識別可能な場合
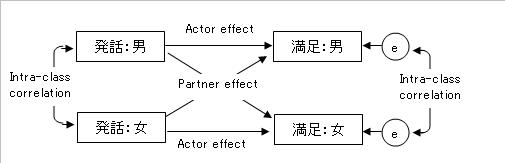
もしデータが、恋愛関係など男女の異性ペアのように、ペア内の個人を識別することができる場合(これを識別可能データと呼びます)、モデリングは非常に簡単です。男性・女性のデータをそれぞれ変数としてSEMのソフトウェアに投入して、下の図のようにパスを引くだけです。制約も必要ないので、簡単。このとき、男性・女性はそれぞれ変数の違いとして表現されるので、サンプル数はペアの数になります。
発話・男から満足・男(発話・女から満足・女)に引かれたパスがActor effectで、発話・男から満足・女(発話・女から満足・男)に引かれたパスがPartner effectです。また、共分散は級内相関(intra-class correlation coefficient)と呼び、ペア内での変数の類似性を表しています。この値が高い場合、ペア内で発話量が類似していることを示しています。誤差についている共分散も級内相関ですが、これは発話量を統制した満足感の級内相関を示しています。
→級内相関については、資料にある論文や心理統計学の記事などを参照ください。
識別可能な場合、男のActor effectと女のActor effectは一致するとは限りません。これらの違いを検討するのも識別可能なデータの目的といえます。
ペアが識別できない場合
さて、やっかいなのはペア内の個人を識別できない場合(これを交換可能データと呼びます)です。同性友人ペア、同性の双子データ、あるいはランダムに設定されたペア(会話実験などは大抵これ)、などがそれに該当します。なぜなら、識別できるデータと違ってカテゴリーに分けることができないので、どっちの個人をどっちのデータにいれればいいか確定しません。仮に入力時の順番に分けたとしても、恣意的になってしまいます(入力の仕方で結果が変わる)。APIMモデルはむしろこのような交換可能データの相互影響プロセスを分析するのが真の目的です。
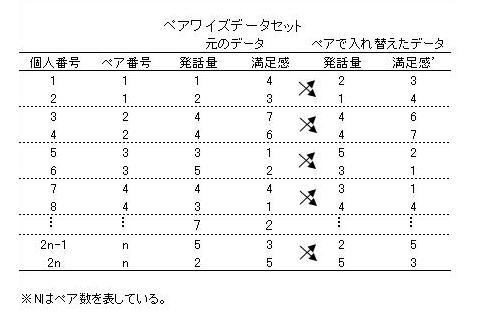
さて、交換可能データを分析するためにはデータセットに工夫を加えないといけません。それは「ペアワイズデータセット」というものを用意します。ペアワイズデータセットとは、ペア内でひっくり返したデータもくっつける、というものです。このデータセットはペアワイズ相関分析などにも使うものです。これらについてはこの論文を参照ください(別ページにPDFの論文が開きます)。
下の図を見ての通り、ペアワイズデータセットはペアの数×2分のサンプルがあることになります。しかし、このようにデータセットを用意することで、データの配置が一意に決まるので「カテゴリー分けの恣意性」をクリアすることができるわけです。
これをこのままSEMに入れたらいいかというと、当然そうではありません。AmosなどのSEMのソフトウェアは普通、データの数でサンプル数を数えます(当たり前)。なので、ペアワイズデータセットのままだとNが2倍になったことになるわけです。
それを避けるために、ソフトウェアにあらかじめ分散・共分散行列+平均ベクトルの状態で入力する方法があります。そうすることで、Nを数値で指定することができるからです。このブログにおいてあるマクロ、HADなどを使えば簡単に分散・共分散行列+平均ベクトルを得ることができます。この出力のNの部分に2で割った数値を入力してソフトウェアに投入すれば、SEMで分析が可能です。
→HADの使い方についてはこちらを参照ください。
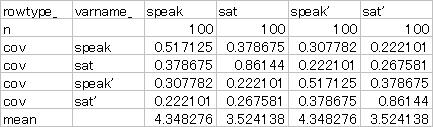
下の図は実際にHADで出力したペアワイズ共分散行列です。仮にペア数が100だった場合、Nのところが200になって出力されるので100に変更しておきます。この共分散行列はそのままAmosに投入できるので、すぐさま分析を行うことができます。
HADでの分析方法
一応、HADでのやり方を書いておくと、
1. ペアワイズデータセットをHADに入力
2. 変数の数を入力
3. 「マルチレベル分析」のチェックをはずす
4. 記述統計オプションの「共分散行列」をチェック
5. 欠損値処理オプションの「リストワイズ削除」をチェック
6. OKを押すと、別のシートにペアワイズ共分散行列(ただしNは2倍)が出力
時間があれば、普通のデータセットから直接、ペアワイズ共分散行列を出力するオプションでもつけようと思います(2010年12月現在は未実装)。
AmosなどのSEMソフトウェアで分析する手順は、次の通り。
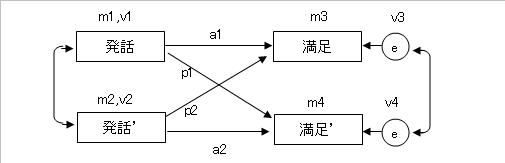
1. まずは下の図のようにパス図を描く。
2. Actor effect同士を等値にする(a1=a2)。
→Amosの場合、パスに同じ記号を入れればOK
3. Partner effect同士も等値にする(p1=p2)。
4. 同じ変数同士の平均値(切片)、分散を等値にする(m1=m2, v1=v2, m3=m4, v3=v4)。
このように制約をかければ、APIMのモデリングは完成です。
パスの値や有意性検定などは普通のSEMと同じように解釈して大丈夫です。APIMでのポイントは、
1.Actor effectとPartner effectの違いを比較する(場合によってはパスの差の検定をしてもよい)。
2.内生変数側の級内相関が、モデル構築前からどれくらい小さくなっているかも注目。
→変数の類似性をどれくらい説明できているかがわかる。
3.同じ変数間の相互因果分析も可能(ただし、双方のパスは等値に制約)。
→同じ変数の類似性を統制した上での、Actor effectやPartner effectが検討できる。
なお、ペアワイズデータセットなので、どうせActor effect同士などは同じ値になるのですが、等値制約をかけるのは適合度計算のための自由度を整えるためです。本来別々に推定するものではないので、等値にしておかないと自由度がその分減ってしまうわけです。
適合度の調整
さて、これで一件落着かといえば、そうではありません。実は上の方法で推定した場合、飽和モデル(パスを可能な限り全部引いたモデル)の自由度は0にはなりません。それは、モデリングで必ず等値制約をかけるためです。もともと同じ変数を無理やり二つに分けて分析しているわけですから、平均や分散の等値制約によってその分、自由度が大きくなります。自由度が大きく見積もられるということは、Χ2検定の結果や、RMSEAやCFIなどの指標が大きく推定されることを意味します。これはよくない。
この問題を解決するためには、まず自由度を調整する必要があります。ややこしい話は抜きにして、次のように自由度(df)を修正します。
当該モデルのdf = 当該モデルのdf - 変数の数×(変数の数+1)
独立モデルのdf = 独立モデルのdf - 変数の数×(変数の数+1)
自由度を修正したら、その他の適合度指標も修正する必要があります。
とりあえずよく使うであろう、CFIとRMSEAの算出式を書いておきます。
CFI = ((独立モデルのΧ2-独立モデルのdf)- (当該モデルのΧ2-当該モデルのdf)) / (独立モデルのΧ2-独立モデルのdf)
RMSEA = sqrt((当該モデルのΧ2/ 当該モデルのdf-1) / ( N- 1 ))
→このときのNはペアの数
なお、上の式で、X2はΧ二乗値を意味しています。
適合度指標の修正が終われば、APIMはようやく完成です。この方法を使うことで、普通ではわからない「交換可能なデータ」における相互影響プロセスを検討することができます。
なにやらややこしそうに見えますが、やってみると思っているよりは簡単です。マルチレベルSEMをAmosでやることを考えれば、楽チンそのもの。ペアワイズデータセットを用意するのはやや面倒ですが、HADで一発でできるようにバージョンアップすればかなり楽になるんじゃないでしょうか。
そんなわけで、Actor-Partner Independence Modelでした。交換可能なペアデータを持っている人は一度チャレンジしてみてはいかがでしょうか。
追記:
交換可能データでも、実はペアワイズデータセットではなく恣意的に並べたデータセットでも、等値制約をちゃんとかけておけば同じ推定値・同じ標準誤差が得られます。つまり、パスの値や有意性検定はペアワイズデータセットのものと同じ結果が出るわけです。つまり、パスの値だけに興味があるなら、わざわざ共分散行列作成→Nを半分にする、という面倒な作業は必要ないことになります。
ただ、ものとデータと構築されたモデルはペアワイズデータセットよりも距離がある(同じじゃないものを等値に設定している)ため、Χ二乗値は不当に大きくなります。つまりは、適合度が真のモデルよりも悪く推定されてしまうというわけです。また自由度も正しくありません。
これらのことから、SEMで分析する以上適合度の計算は必須なので、ペアワイズデータセットを使わない方法はオススメできません。
難しいことは置いといて手っ取り早くAPIMをやってみたい、という場合には、上記の方法は有効かもしれません。そのモデルで十分適合度が高いなら、ペアワイズデータセットで分析しても適合度はいいはずなので。最終的に報告するときはペアワイズデータセットで分析しなおすといいでしょう。