尺度を作った時など、因子分析で因子をいくつ抽出すればいいか悩むことがあるかと思います。
因子分析の因子数決定には、従来では以下のような基準が定番でした。
- ガットマン基準:固有値が1以上の因子を採用する
- スクリー基準:固有値の大きさをプロットし、推移がなだらかになる前までを抽出する
- 寄与率が50~60%以上になる因子数を採用する
- 解釈が可能な因子構造を採用する
1のガットマン基準が最も使われていると思われますが、この方法は最近ではあまり良い方法とはみなされてはいないようです。もしデータが母相関行列であるならこの方法は適切ですが、実際のデータには誤差が含まれるので多すぎたり少なすぎたりする因子数を提案してしまいます。
この記事では、因子数決定に使える基準について述べます。
興味のある人は続きを読んでください。
因子分析は少数の因子によって、変数の相関関係を説明する方法です。
つまり、何因子用意すれば、「きれいにデータの相関を説明できるか」、というのが因子数選択においてポイントになります。
このとき、因子数が多すぎると推定するべきパラメータが増えて結果の再現性が怪しくなります。
少なすぎると、データとモデルの距離が離れすぎてしまって、適切なモデルとはいえなくなります。
そこで、以下のような様々な方法が検討されています。
詳しくは堀先生のHPを参照してみてください。ここではわかりやすさ重視で解説します。
情報量基準
そこで有効なのは情報量基準などの適合度を参照する方法です。
最尤法を使った場合は、χ2(カイ2乗)値などが出力されますので、それを基にAICを簡単に算出できます。
変数の数をp、モデルの自由度をDFとすると、
AIC = χ2 + 2*((p^2-p)/2-DF)
で求まります。AICはデータとモデルの距離を表すもので、小さいほどモデルの当てはまりがよいことを意味します。
もし計算が面倒であれば、
AIC' = χ2 - 2*DF
を比較しても、結果は変わりません。こちらのほうが計算が楽なので便利です。
ただしAICはモデルが複雑なものを採択しやすいので、因子数は多くなりがちです。
そこで、よりパラメータ数のペナルティを大きくするBICのほうがいいかもしれません。
(追記:堀先生のページによると、AICよりはBICのほうが「因子数決定において」はいいようです)
BIC’ = χ2 - log(n)*DF
ここで、nはサンプルサイズです。AICの2の代わりに、サンプルサイズの対数を自由度にかけたものを補正に使うわけです。
これらの方法は、SPSSなどの汎用ソフトの出力から簡単に計算できるので、利用可能性が高いです。
また、χ2検定は、サンプルサイズが大きいとどんなモデルも棄却されてしまうので、あまりお勧めはしません。
平行分析
因子分析では、相関行列の固有値を計算することで分析します。ここで、固有値とは何か?という問題に答えると線形代数の本一冊分の文章を書かないといけないので、ここでは数学的な説明は省きます。
因子分析における固有値は、いうなれば抽出した因子の「情報量」を意味します。正確に言えば分散です。
なので、もしデータがきれいな因子構造を持っていれば、モデルで想定した因子以外の情報量は0になるはずです。
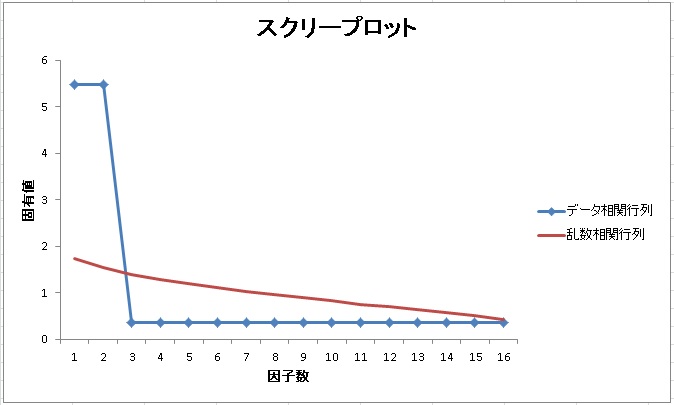
例えば、完全な2因子モデルを想定した相関行列の固有値の推移は以下のようになります。
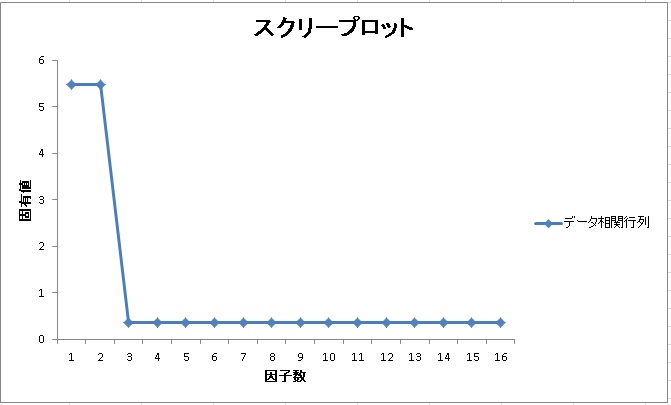
2つの固有値が突き抜けていて、他の因子は0に近くなっています。
しかし、実際には相関行列には誤差が含まれているので、こんなにきれいな固有値の推移にはなりません。
なのでどこまでが意味のある情報を持った因子で、どこまでが誤差による因子なのかが判別しづらいのです。
そこで、データに含まれている誤差を推定して、誤差よりも大きな情報を持った因子数を抽出しよう、というのが平行分析です。
平行分析では、データと同じサンプルサイズの乱数をたくさん発生させます。そして、その乱数同士の相関行列の固有値を計算して、データと同様にプロットするわけです。
すると、以下のようなまっすぐな線がプロットされます。
赤い線が乱数による相関行列の固有値です。この赤い線とデータの固有値の推移が交わったところ以上の因子が、「意味のある因子」として判断します。
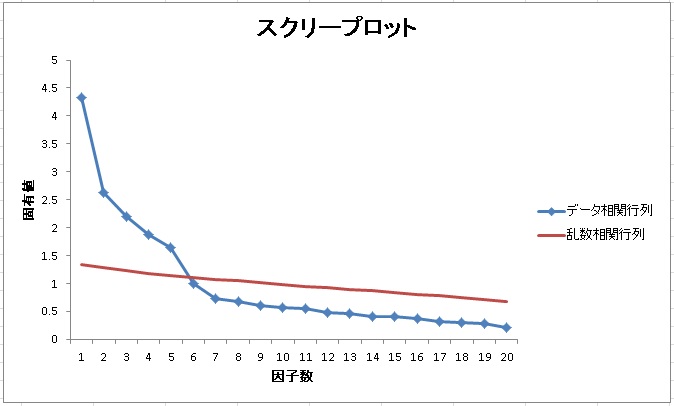
では、実際にBIG5(5因子が仮定されるパーソナリティ尺度)を因子分析した場合のスクリープロットと、平行分析による乱数のデータのスクリープロットを重ねてみましょう。データは580人です。
スクリープロットは5因子と6因子の間で交わっています。このことから、仮説通り5因子を採用することが提案されます。
平行分析はRのpsychパッケージに含まれている、fa.parallel()関数で実行が可能です。また、このブログにあるHADでも可能です。
平行分析にもいくつか種類があり、共通性を事前にSMC(各変数とそれ以外の変数の重相関係数の2乗)で推定したものを対角項に入れた相関行列を用いるものがあります。この方法も強力で、一見、見落としがちなマイナー因子を抽出してくれる時があります。対角SMCによる平行分析は、因子数を多めに提案しますが、意外と解釈できる構造である場合があります。
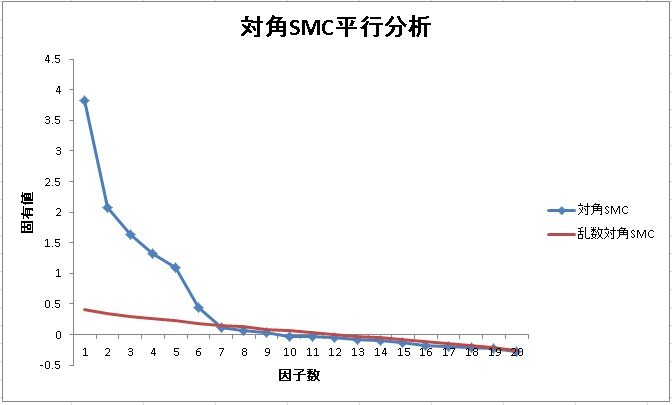
例えば、先ほどのBIG5データを使って、対角SMC平行分析を行うと以下のようになります。
さきほどと違って、今回は6因子が提案されています。実際に6因子で因子分析をしてみると、情緒不安定性の因子が順項目と逆転項目で2つに別れました。研究目的によっては、このような分け方も妥当である場合があります。
このように対角SMC平行分析は、採用しうる最大の因子抽出数を提案している可能性があり、なかなか便利です。
追記:
堀先生の研究によると、相関行列を使う普通の平行分析は、因子間相関が高い場合に因子数を過少推定する傾向があるようです。因子間相関が高い場合、理論的に同じ因子としていいかどうかは実質科学的知見によると思います。より妥当な判断をするためには、これらの指標の特徴をよく理解する必要があるようです。
また、対角SMC平行分析は、過大推定はするが過少推定はほぼしない、という特徴をもっています。このことから、対角SMC平行分析は最大の因子数の基準として使うといいでしょう。
MAP(最小平均偏相関)
次に、因子によってデータの相関をきれいに説明する、というコンセプトを体現した指標を紹介します。
それが、MAPです。
MAPとは、Minimum Average Partial(correlation)の略で、つまり最小の平均偏相関という意味です。
因子分析が適切であれば、因子を統制した項目間の偏相関は0に近づくはずです。もし因子が少なかったり、過剰に大きければ、偏相関は高いままです。このことを利用して、因子を統制した後の偏相関の平均を算出し、それが最小となる因子数を選択しよう、というのがMAPです。
MAPを算出してくれるソフトウェアは残念ながらあまりありませんが、服部先生の「忍者はっとりくん」が算出してくれます。あと、以下で述べるようにHADも出力します。
追記:
阪大の林さんからコメントいただきました。RのpsychパッケージにあるVSS()関数もMAPを計算するようです。psychパッケージはとても便利ですね。
MAPは、小項目のマイナー因子(2,3項目で構成される因子)はあまり検出せず、どちらかといえば倹約的な因子構造を提案します。できるだけ少ない因子でモデルを構築したい場合に、MAPの提案する因子数を採用するといいでしょう。
それでは、先ほどのBIG5データでMAPを計算してみましょう。HAD9.16での結果です。
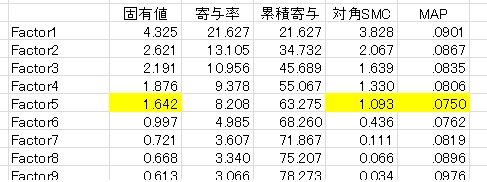
黄色いところが提案ポイントです。MAPは平行分析と同様に5因子を提案しています。(対角SMCの基準は、固有値の合計がSMCの合計よりも大きくなった因子数を提案するものです。考え方はガットマン基準とほぼ同じです。)
個人的には、MAPはかなり強力だと思います。従来の方法では抽出しにくかった仮説因子モデルを提案してくれることが多い印象があるからです。
追記:
MAPの特徴としては、過少推定はするが、過大推定はほぼない、ということらしいので、最小の因子数の基準にするとよいでしょう。
各提案が分かれるとき
堀先生の提案としては、MAPを最小抽出数、対角SMC平行分析を最大抽出数にして、その間で決定する方法があげられています。つまり、MAPと対角SMC平行分析の提案数が一致すれば、かなり安定した因子モデルだといえそうです。
あとは研究目的にもよります。初めから先行研究で少数の因子構造が仮定されているなら、MAPは強力です。それに対して、尺度を作成している最中で、いろいろ情報を吸い上げたい場合は対角SMC平行分析が有効です。マイナー因子もひろい上げてくれるので、いろんな発見につながります。
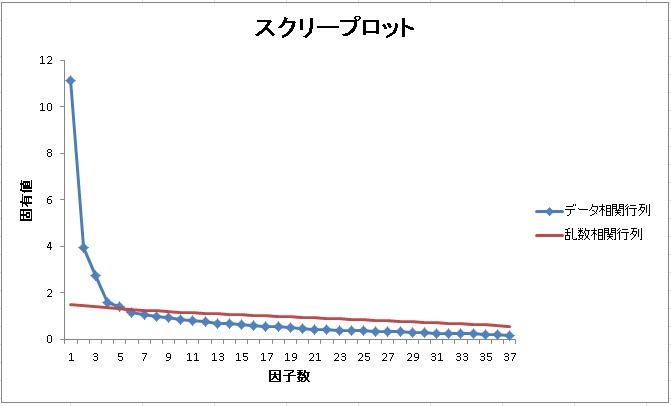
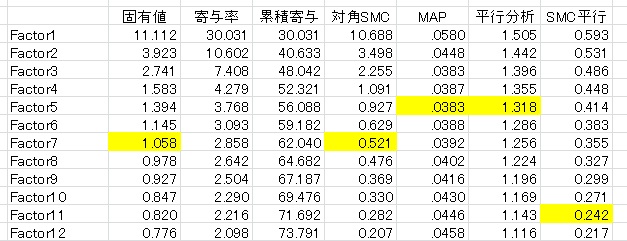
例えば、以下のようなデータが得られたとします。このデータは3因子が仮定された37項目の尺度です。スクリープロットと平行分析、MAPの結果を見てみましょう。
MAPと平行分析は5因子を、対角SMCは11因子を提案しています。
ただ、MAPは3因子と5因子にはほとんど違いがありません。理論仮説とMAPを参考にするなら、3因子を採用するのもいいでしょう。ただ、3因子ではとらえきれないマイナー因子が2因子あることがうかがえます。
さすがに対角SMCが提案している11因子は多すぎる印象があります。しかし、逆に言えばこのデータがそもそも多く誤差を含んだデータである可能性を示唆しているかもしれません。実際に5因子で分析してみると、第3因子が二つに分かれ、第2因子のうち2項目だけがマイナー因子を形成していました。
この場合、解釈可能ならマイナー因子を省いて4因子で再分析してみるのもいいかもしれません。
なお、ガットマン基準が示している7因子は、解釈ができない構造(どの項目も負荷しない因子がある)でした。
総合的に判断して、MAPが提案する3因子か5因子を採用するのがよさそうです。
これまで説明してきたように、これまでのような誤差を含んだガットマン基準や、視覚的な判断であるスクリー基準は、あまり有効ではありません。
最近では、さまざまな因子数決定方法が提案されていますので、Rなどを利用している人はそれらの方法を活用するといいでしょう。
堀先生の論文の引用は以下。
堀 (2005). 因子分析における因子数決定法 -平行分析を中心にして- 香川大学経済論叢, 77, 65-70.