勢いにのって、今年2本めの記事です。
今回は、多次元展開法をベイズ推定しようという話を書きます。
◆多次元展開法とは
そもそも多次元展開法を知ってる人がかなり少ないのではないかと思います。多次元尺度法のこと?と思う人も多いでしょう。似てますが、少し違います。
多次元尺度法は、対象間の距離データから、その対象をD次元ユークリッド空間にマッピングする手法です。消費者行動研究とか、犯罪心理学とかでよく使われます。
一方で多次元展開法は、回答者と対象との距離データから、対象と回答者を同じ空間にマッピングする方法です。百聞は一見にしかずということで、足立(2000)の計量多次元展開法の結果の図を貼ってみましょう。
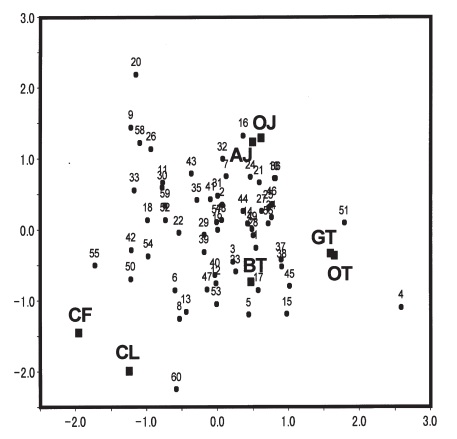
足立(2000)計量多次元展開法の変量モデル 行動計量学, 27, 12-23.の図3から引用
上の図は、7つの飲み物と、60人の回答者をマッピングしたものです。OJ(オレンジジュース)、AJ(アップルジュース)、GT(緑茶)、OT(烏龍茶)、BT(紅茶)、CF(コーヒー)、CL(コーラ)について、回答者にどれくらい好きかを0~10で評定してもらったデータを使っています。なんとなく、刺激が強い系、曖昧もの系、お茶系、というように飲み物の好みが分かれているように解釈できそうです。つまり、60×7のデータについて分析をすると、上のようなマッピングができるのが多次元展開法というわけです。なお、この論文にデータも全部載ってます。
ただ、ここで注意が必要なのは、好みを回答者と対象の心理的な距離であると定義していることと、その測定が間隔尺度として測定されるという仮定がある点です。この記事ではそれらの点についてはつっこまず、素直に「そうなのね」と受け入れます。
なんか、めっちゃ楽しそうな分析ですよね(雑な感想)。なんでこんな楽しそうな方法があまり心理学で注目されてこなかったかが気になりますが、実は理由があります(長いので次の段落は読み飛ばしてもよい)。
もともと提案された古典的展開法(Coombs, 1950)やその発展である古典的多次元展開法は、推定がめっちゃ難しかった。で、それを距離について計量的に測定できるという仮定の下で線形代数的に整理して簡単にしたのが計量多次元展開法(Schonemann, 1970)です。これで一応推定はできたんですが、今度は多次元展開法特有の問題として、縮約解という、全部の回答者座標が中点に集中してしまうという問題が生じ得ることがわかりました。この原因はいろいろあるとおもいますが、一つは展開法がサンプルサイズが増えると同時に未知数の増え続けるという問題です。それは対象の座標点に加えて回答者の座標点も同時に推定するからです。とくに、多次元を仮定している場合1つのサンプルを増やすとD次元あれば、D個の未知数が増えていきます。個人に複数の回答データがあれば一応は推定できるはずですが、どうしても推定結果が不安定になります。
そこで、階層モデルを仮定すればその問題が解決できるのでは?というアイディアがでてきて、その結果、回答者パラメータに確率モデルを設定する多次元展開法の変量モデルが提案されました。それについてもいくつかモデルがあるんですが、その一つに上で紹介した足立(2000)の計量多次元展開法の変量モデルがあります。余談ですが、展開法は日本の心理統計学者がたくさん研究に関わっているのが特徴で、足立先生以外に高根先生や岡本先生、Hojo先生(漢字わからなかった)などが研究してます。
というわけで、足立(2000)で提案されている、多次元展開法に変量モデルを仮定した方法だと、うまく推定できるようになったというわけです。ただ、多次元展開法の変量モデルについて、Rなどをはじめ、一般的な統計ソフトウェアには推定のためのプログラムの開発がされていません。なので、面白そうだなと思っても、一般的なユーザーが実際に分析できる環境にはなかったわけです。
そこで、Stanで多次元展開法を推定できると便利なのでは、ということでこの記事の話になります。
◆多次元展開法をベイズ推定しちゃおう
多次元展開法は変量モデルを使えばうまく推定できるということで、それならベイズ推定を使えば簡単なんじゃないかというのが今回の記事のモチベの一つです。というわけで、上で紹介した足立(2000)のモデルをStanで推定してみましょうというものになります。なお、ベイズによる多次元展開法についてもいくつか研究があります。
多次元展開法をベイズで解くことのメリットはそこそこあります。1つは、変量モデルを使う場合、最尤法だと周辺化する必要があるんですが、多次元を仮定する場合次元の呪いに陥ります。つまり、高次元になるほど推定精度がどんどん落ちていきます(数値積分の分割がものすごい必要になる)。この問題は、ベイズを使えばある程度は解決します。もちろん推定パラメータ数が増えるので規模がどんどん大きくなりますが、推定精度自体はそんなに問題にならないと思います。
もう一つはMCMCの特徴として、事後分布が手に入るので信頼区間などが簡単に計算できるとか、モデルの拡張がしやすいとかがあります。
ベイズ推定するためには確率モデルと事前分布がいるので、簡単に書きます。まず、選好データが正規分布に従うとして、それが次のように対象と回答者の距離によって構造化されていると仮定します。
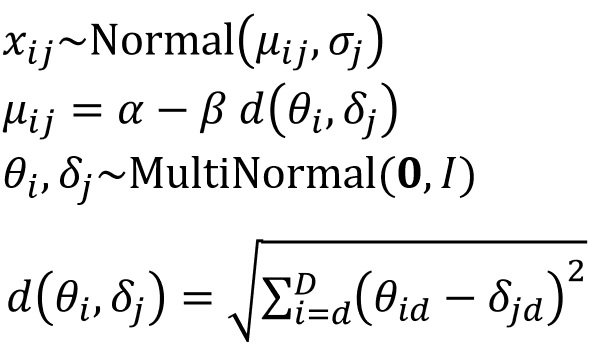
ここで、θは回答者のD次元の座標点、δは対象のD次元の座標点を表します。距離関数dは、ユークリッド距離を仮定しています。δとθは多次元標準正規分布を事前分布としておきます。ここでIは単位行列です。αとβ、そしてσは適当に事前分布をおいて推定します(おい)。なお、σは項目ごとに推定されます。
確率モデル自体はシンプルで、すぐにでもStanに実装できそうですが、ここでMCMCで多次元展開法を解くための工夫がいろいろいります。これが結構大変だったりします。この辺の問題の解決が難しいので、ベイズ推定の方法もあまり知られてないのかな・・・とも思ったり。
◆多次元展開法を解くためのパラメータの制約と、事後的な処理
まず、多次元尺度法でもそうですが、D次元ユークリッド空間にマッピングするとき、δとθには3つの不定性があります。
1.原点の不定性
2.回転の不定性
3.符号の不定性
原点の不定性は、どの点を中心とするかについての問題です。データとしては対象と回答者の距離しか与えられていないので、マッピングの結果、どこが中心であってもデータへの適合は変わりません。それと同じことが、回転と符号についてもいえます。
そこで、1の原点についてはδを各次元ごとに総和を0にするという制約をおくことで解決します。つぎに2の回転については任意の要素の値を次元数‐1個だけ特定の値に固定することで解決します。多くの場合、2次元目は要素1番目の対象の座標点を0に、3次元目は1と2番めの対象の座標点を0に固定する、という感じで制約します。
そして、3番目の符号の不定性については、MCMCでは制約が難しいので、サンプリングしたあとで対処するのが良いです。いろんな方法がありますが、この記事では、事後的にプロクラステス回転をする方法を提案しておきます。まず、MCMCのチェイン数を奇数にして(今回は5)、事後分布のMAP推定値をターゲット行列にしてMCMCサンプル全部についてプロクラステス回転をします。そうすると、符号はMAPにあわせられるので、単峰の事後分布が得られるようになります。詳しくはデモで解説します。
◆Stanコードと実際の推定
それでは、上の方法で推定してみましょう。計量多次元展開法の変量モデルは、次のStanコードで実装できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
functions{ vector sum_to_zero(vector y){ int n = rows(y)+1; real norm = sum(y)/(sqrt(n)+n); real fill_val = norm - sum(y)/sqrt(n); vector[n] x = append_row(y,fill_val)-norm; return(x); } matrix sum_to_zero_tri_matrix(vector delta_raw,int M, int D){ matrix[M,D] delta; matrix[M-1,D] tempmat; int v = 0; for(d in 1:D){ for(m in 1:(M-1)){ if(m < d){ tempmat[m,d] = 0.0; }else{ v += 1; tempmat[m,d] = delta_raw[v]; } } delta[,d] = sum_to_zero(tempmat[,d]); } return(delta); } } data { int int int matrix[N,M] Y; } transformed data{ int V = to_int((M-1)*D - (D^2-D)/2); } parameters{ vector[V] delta_raw; matrix[N-1,D] theta_raw; real alpha; real vector } transformed parameters{ matrix[M,D] delta = sum_to_zero_tri_matrix(delta_raw,M,D); matrix[N,D] theta; for(d in 1:D){ theta[,d] = sum_to_zero(theta_raw[,d]); } } model{ for(n in 1:N){ vector[M] mu; for(m in 1:M){ mu[m] = alpha - beta * distance(theta[n,],delta[m,]); } target += normal_lpdf(Y[n,] | mu,sigma); } // delta prior target += std_normal_lpdf(delta_raw); // theta prior target += std_normal_lpdf(to_vector(theta_raw)); // other prior target += normal_lpdf(alpha | 0, 10); target += exponential_lpdf(beta | inv(10)); target += exponential_lpdf(sigma | inv(10)); } |
モデルの簡単さに比して、ややコードが長いですね。ポイントは、原点の不定性をなくすためにsum_to_zero関数を定義していること(これについてはすでに記事を書いているので、そちらを参照してください)、そして回転の不定性を消すために上三角を0に舌行列を作ったうえで、sum_to_zeroの処理をする関数を定義していることです。詳しくはコードをがんばって眺めてください。
なお、回転の不定性はδだけに与えておけば、大丈夫です。ただ、原点の不定性はθについてもなくしておかないとうまく収束しません。このあたりはいろいろ試してみてわかってきたことですね。頑張った、俺。
それでは、足立(2000)のデータを使って分析してみました。Rコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
drink <- read.csv("data/drink_data.csv") N <- nrow(drink) M <- ncol(drink) D <- 2 datastan_rmu <- list( N = N, M = M, D = D, Y = drink ) model.rmu <- cmdstan_model("model/MU.stan") chains <- 5 fit_rmu <- model.rmu$sample( datastan_rmu, iter_warmup = 1000, iter_sampling = 1000, chains = chains, parallel_chains = chains, thin = 1, refresh = 100 ) |
これで2次元モデルを推定できます。
◆次元数についてのモデル比較
さて、足立(2000)ではAICでモデル比較をしていますが、今回はパラメータを周辺化していないことから、AICやBICでは正しくパラメータ数についての罰則を与えられません。そこで、ブリッジサンプリングを使って、-2対数周辺尤度を計算してモデル比較をしてみます。-2をかけているのは、AICやBICと同じスケールにするためです。
ブリッジサンプリングをcmdstanrでやる方法については別の記事を書いているので、そちらを参照してみてください。
Rコードは以下ですが、cmdstanr_bs関数などは上の資料のものを使っています。このあたりの関数たちはまとめてアップしてるのでそちらを見てもらえれば。
|
1 2 3 4 5 6 7 |
datastan_rmu$D <- 1 chains <- 5 fit_rmu_D1 <- model.rmu$sample(datastan_rmu,chains = chains,parallel_chains = chains, iter_sampling = 10000,refresh = 1000) logprob1 <- make_logprob_fit(model.rmu,datastan_rmu) bs1 <- cmdstanr_bs(fit_rmu_D1,logprob_fit = logprob1) |
こんな感じ。たぶんこれだけだと何やってるかさっぱりわからないと思いますが、上のブリッジサンプリングの記事を見て(何回言うねん)。これを1次元~4次元で比較してみました。結果は以下の通り。
|
1 2 3 4 5 6 7 8 |
> -2*logml(bs1) [1] 1962.653 > -2*logml(bs2) [1] 1956.381 > -2*logml(bs3) [1] 1955.026 > -2*logml(bs4) [1] 1956.941 |
足立(2000)のAICの結果では、2次元が最小になっていましたが、今回の結果では3次元が一番予測力があるようです。というわけで3次元で推定した結果を報告します。
◆MCMCの推定後の処理
まず、lp__の事後分布を見てみましょう。
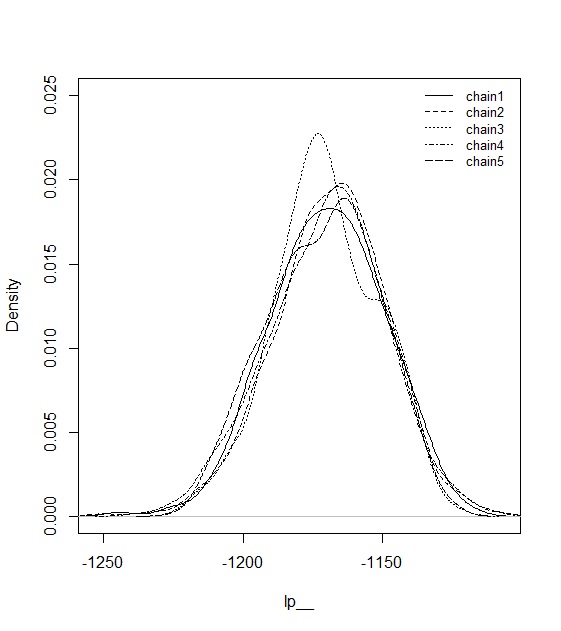
まぁちょっとズレてるとこありますが、いい感じでしょうか。いままでいろんなデータでやってみましたが、計量多次元展開法はwarmup=1000, sampling=1000で十分なことが多いです。推定時間もそんなに長くはないです。
ただ、δの事後分布を見ると大変です。
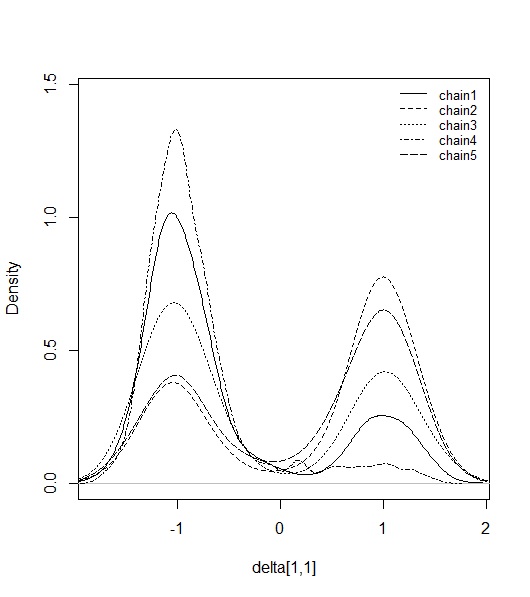
あばばばば えらいことになってます。でもこれは、符号の不定性によって生じていることで、実はMCMC自体は収束しています。チェイン数を奇数にしておけば、正負どちらかの点のMAPが顕著に高くなるはずなので、それに対してプロクラステス回転をやります。すると、次のようになります。
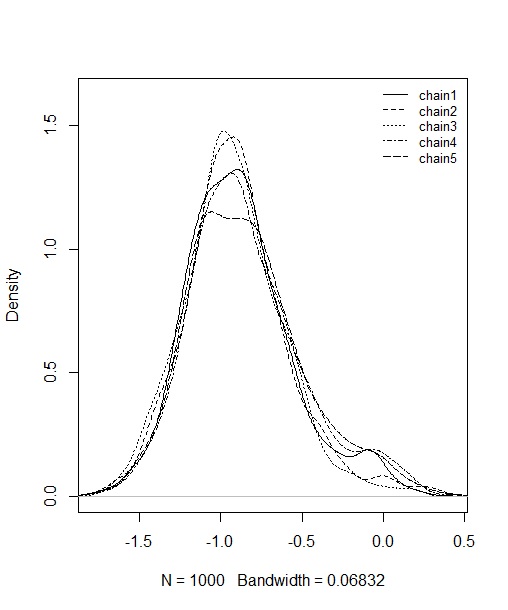
ちゃんと-1あたりに全部のMCMCサンプルが移動してくれました。このあたりのコードもアップしているので、そちらを見ておいてください。なお、θについても同様に符号の不定性があるので、δとθを同時に回転させておくと良いでしょう(別々にしないこと)。
さて、3次元のうち、第1と第2次元についてプロットしてみます。図は、第1次元の2乗和が最大になるように回転させてます(もと論文と一致するように)。
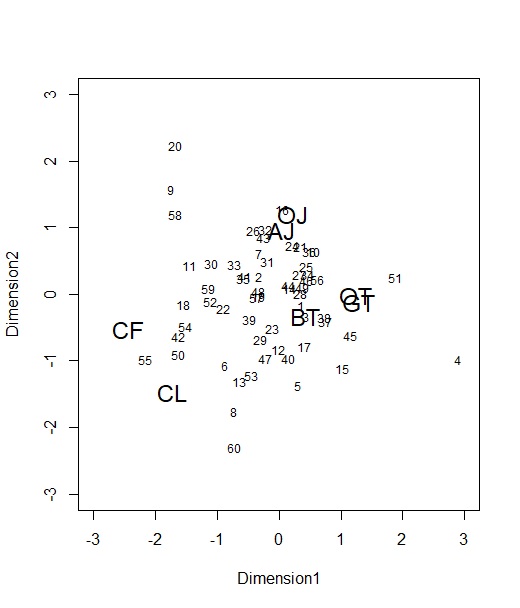
どうでしょう、ほぼほぼ、上の足立(2000)の結果を再現しています。ただ、CF(コーヒー)の位置がちょっと中心によってますかね。これはδにも事前分布をおいている影響だと思います。
ついでに、第1と第3次元もプロットしてみましょう。
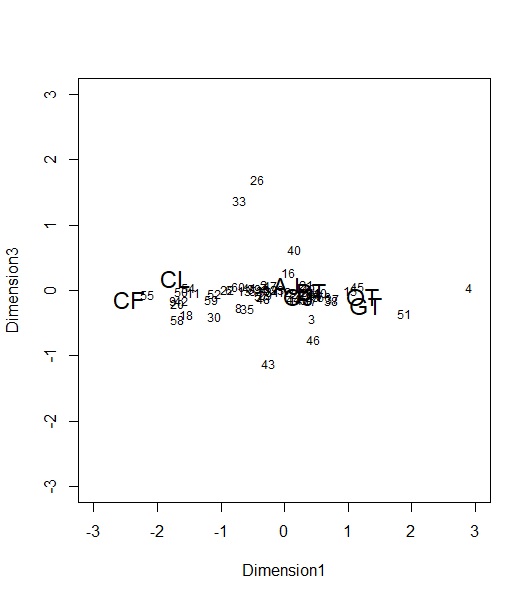
第3次元が縦軸ですが、かなり分散が小さいですね。ほぼほぼ2次元で説明できてそうですが、一部の人(26とか33、43の人)が2次元では収まらない選好を持っているのがわかります。
この分析をするためのコードをこちらのOSFプロジェクトにあげてますので、興味ある人はダウンロードして、自分で分析してみてください。データごとRstudioのプロジェクトフォルダをアップしているので、Zipでダウンロードして解凍すればそのままRで分析できると思います。