HAD9.3から、ロジスティック回帰分析ができるようになりました。
ロジスティック回帰分析とは、目的変数が「0と1」のような、2値データの場合に用いる回帰分析の一種です。
例えば、反応がある・反応がないといった、連続的ではなくある・なしのどちらかしか結果が出ないようなデータを目的変数にする場合に用います。
なぜ2値データの場合では回帰分析ではなく、ロジスティック回帰分析を使うのかといえば、理由は2つぐらいあります。
- 予測値が0より小さい、あるいは1より大きな値が生じるから
- 回帰分析が「残差が正規分布になること」を仮定しているから
1.については、値が0か1にしかならないようなデータで、予測値が2.5とかでてきても、予測として意味がない、ということです。つまり、一番小さくて0、一番大きくて1になるような予測値が計算できるモデルを使う必要があるわけです。
2.については、残差の正規性という仮定がある普通の回帰分析では、信頼区間の推定に誤りが生じます。
0と1しか生じないデータなので、残差も正規分布になるわけがありません。このようなデータを回帰分析で分析しても、検定結果は正しくありません。これらの理由から、普通の回帰分析を利用することは不適切です。
そこでロジスティック回帰分析の登場です。
ロジスティック回帰分析は、モデルに線形を仮定せずに、シグモイド曲線を仮定します。
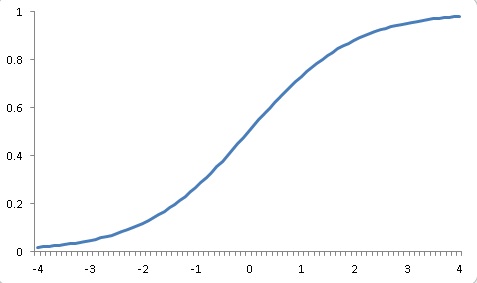
シグモイド曲線とは、下の図のような曲線で、ある一定の範囲に収まります。
特に、ロジスティック曲線は0~1の間に収まります。
図からわかるように縦軸は0~1の間に収まりますが、横軸(ロジット得点)は連続的で、最小と最大はそれぞれ無限になります。よって、モデルによる予測値が大きくなっても、変換すればちゃんと0~1の範囲に収まるということです。具体的には、例えば値が2.5となっても、ロジスティック関数で変換すれば0.92ぐらいになります。
このように、0~1の範囲のデータでも、ロジスティック関数を使えば回帰分析と同様の線形モデルによる予測ができるようになります。
またロジスティック関数の逆関数をロジット関数といいますが、これは正規分布関数にとてもよく似た関数です。この関数の分布(ロジット分布)を使えば信頼区間も同様に推定が可能です。つまり、誤差が正規分布にならずとも、ロジット分布に従うと考えれば検定も同様に可能です。
【訂正】ロジスティックの誤差はロジット分布にはなりません。二項分布になるようです。
ロジット分布に従う得点のことをロジット得点、あるいは単にロジットといいます。標準正規分布に従う得点のことをz得点といいますが、それのロジスティック版だと思えばOKです。標準得点も、得点と確率に一定の関係がありますが、それと同じように、ロジットもロジット分布に従った確率の関係があるのです。
このように、ロジスティック回帰分析は、ロジットを対象に線形回帰を行う方法です。ロジットは確率に変換すれば0~1の間に収まるので、予測値が1を超えることがありません。これで回帰分析の問題はすべて解決、というわけです。
※ロジスティック曲線でなくても、例えば累積正規曲線でも同様に0~1の値を予測することができます。
累積正規分布を用いた方法は、プロビット回帰分析と呼びます。そのほかにも、さまざまなシグモイド曲線による非線形回帰分析が提案されています。
ロジスティック分布がよく使われるのは、1.計算が簡単だったこと、2.後述するオッズ比に変換できること、などが利点としてあるからだと思います。
さて、では実際にHADでロジスティック回帰分析を実行する方法を解説します。
続きをどうぞ。
HADの基本的な使い方は、こちらの記事を参考にしてください。
また、基本的な方法は回帰分析と同じなので、先にHADで回帰分析をする方法などの記事も参照してください。
まず、モデリングシートの「回帰分析」ボタンを押して、回帰分析のモデリングスペースを開きます。そして,「回帰分析」「分散分析」「一般化線形モデル」「階層線形モデル」という4つのオプションボタンがありますが,そのうち,「一般化線形モデル」を選択してください。
次に,目的変数の種類を選択抱きますので,「順序」を選んでください。これは目的変数の尺度水準が順序尺度であることを指定しています。これでロジスティック回帰分析が実行できます(2値でも順序でも同じアルゴリズムで分析できます)。
そして目的変数(もちろん、2値データの変数)を指定します。
2値データは0と1である必要はありません。1と2でも、小数点があっても,なんでもOKです。
上の図のように、回帰分析のモデリングスペースに目的変数と説明変数を指定します。
このとき、idt_dは0と1だけが入力されているデータです。説明変数のtalk2とperは連続的な変数です。
この状態で「分析実行」ボタンを押せば、ロジスティック回帰分析を実行します。
なお、HADでは推定法は最尤法を用いています。
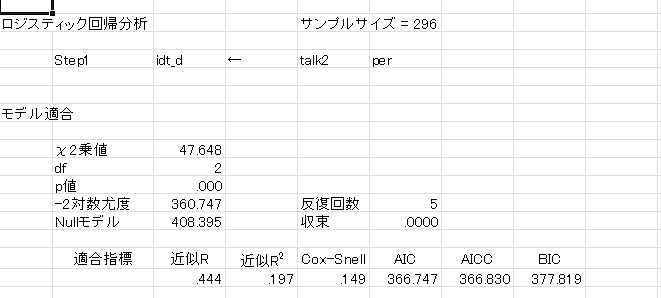
上の図のような結果が出力されます。
◆モデル適合について
モデル適合は、対数尤度から計算したχ2乗値と自由度、確率が表示されます。
この確率は、説明変数を投入したことによる逸脱度の減少度合いが0であるという帰無仮説に対する確率です。つまりは、モデル説明率が0であるかどうかについての検定です。
-2対数尤度は逸脱度を表していて、モデルとデータの乖離の程度を表しています。大きいほど適合が悪いことを意味しています。
Nullモデルとあるのは、切片だけを推定した場合の逸脱度で、モデルの逸脱度からNullモデルの逸脱度を引いたものが、モデルのχ2乗値になります。すなわちモデルのχ2乗値は、説明変数を投入することによるモデルの改善の程度を表しているといえます。
適合指標にある、近似R2は、回帰分析のR2乗値とよく似たもので、分散説明率を表しています。Cox-Snellは尤度に基づく説明率の指標で、回帰分析を適用した時に近い値が計算されます。しかし、最大値が1にならないという欠点があります。
◆回帰係数について
回帰係数は、説明変数が1点増えた時の、ロジット得点の変化量を意味しています。
標準ロジスティック分布の分散はπ^2 / 3 なので、 標準偏差はだいたい1.8程度です。
おおまかにいえば、標準偏回帰係数の1.8倍ぐらいの大きさになるということです。
(ただし、分布の形が微妙に違うので完全に一致しません)
◆オッズ比について
HADでは、以下のようにオッズ比も出力します。ロジスティック回帰分析の場合は、回帰係数の大きさよりもオッズ比のほうが解釈しやすいかもしれません。
まず、オッズについて説明します。
オッズとは、確率の別表現で、「起こる確率と起こらない確率の比」みたいなものです。
式は p / (1-p) で求まります。
確率50%で起こる(つまり50%で起こらない)場合は、オッズは1になります。これが基準です。
ここで、確率が60%なら、0.6 / (1-0.6) で1.5になります。これは、起こる確率の方が起こらない確率より1.5倍高いことを意味しています。このように、オッズは、一方の出来事がもう一方の出来事よりも何倍起こりやすいかを表す指標になっているわけです。
また、ロジットとオッズは、対数の関係にあります。ロジットはオッズの自然対数になり、逆にロジットのe(自然対数の低)の指数関数がオッズになります。
さて、オッズ比について。ロジットとオッズの関係は上に述べたとおりですが、ロジットの差とオッズの差も同様に考えることができます。もともと回帰係数は得点の差を意味しますから、オッズも差として考えなければいけません。そのような差は、オッズ比と呼びます(対数にすると比が差になることを思い出しましょう。つまり、ロジットの差は、オッズでいうところの比になります)。
難しく考えずとも、オッズ比はオッズと同じような解釈ができます。つまりは、二つので出来事を比較して、どちらが何倍起きやすいかを表している、ということです。ロジスティック回帰分析の観点からは、説明変数が1点増加すると、オッズがどう変化するかを表しているのがオッズ比です。
例えば、上の図ではtalkはオッズ比が1.368ですが、talkが1点増えると、目的変数が0ではなく1になる確率が1.368倍増える、ということです。
◆交互作用項の投入
HADのロジスティック回帰分析は、回帰分析と同じように交互作用項も検討ができます。
下の図のように、*で変数をつなげば、交互作用項になります。
また、スライス変数に変数を指定すれば、スライス変数が高い群と低い群での回帰係数をそれぞれ推定します。
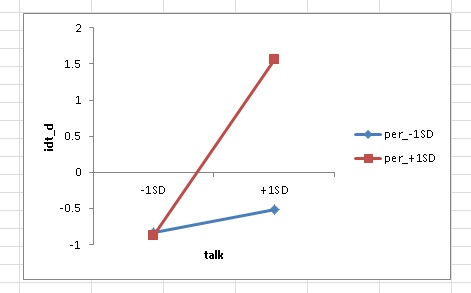
交互作用効果のグラフも表示します。
グラフの縦軸はロジットです。
◆ステップワイズ法
回帰分析と同様に、ロジスティック回帰分析でもステップワイズ法が可能です。
やり方は回帰分析と同じですので、こちらの記事を参照してください。
HADのメインページに戻る