次に、回帰分析の応用である階層的重回帰分析を実行する方法について説明します。
階層的重回帰分析は、回帰分析をいくつかのステップに分けて実行する方法です。例えば、メインの説明変数以外に統制しておきたい変数群(人口統計学的な変数など)がある場合、それらの変数群を統制したうえでの説明変数群の説明力を検討したいことがあると思います。
そのようなとき、ステップ1で統制変数群を投入し、ステップ2でメインの説明変数群を投入することで、ステップ1からステップ2においてどれほど説明力が増加したかを検討することができます。これが階層的重回帰分析です。
また、最近の社会心理学・パーソナリティ心理学では回帰分析を使って交互作用を検討することが増えてきました。そういった場合にも階層的重回帰分析が利用されます。
それは、まず主効果をステップ1に投入し、交互作用効果をステップ2に投入することで、交互作用効果全体の説明力がわかります。あるいは、1次の交互作用、2次の交互作用のどこまで投入すべきかを情報量基準などを参考に決定することもできます。
このように、ステップごとに説明力やモデル適合などを比較して、効率の良いモデル選択を行うことができるのが階層的重回帰分析なのです。
それでは、具体的な方法を続きで説明します。
◆統制変数をステップ1に入れて、メインの説明変数をステップ2に入れる分析
回帰分析の方法自体は、「HADで回帰分析をする方法」をご覧ください。
ここでは、以下のようなダミーデータを使って説明します。
このダミーデータは、集団課題実験のデータで、課題中の発言量や課題のパフォーマンスが集団への帰属意識(集団アイデンティティ)に及ぼす影響を見る、というストーリーです。
各変数名は、
- idt:集団アイデンティティ
- talk:発言量
- per:課題のパフォーマンス
- skill:参加者のコミュニケーションスキル
です。
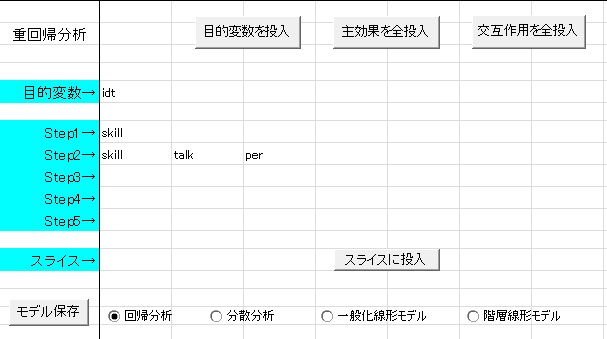
ではまず、idtに及ぼす発言量とパフォーマンスの影響を見てみましょう。そのとき、コミュニケーションスキルを統制変数にして、そのほか二つの変数の説明力を検討してみます。まずskillをステップ1に、talkとperをステップ2に指定するのですが、ステップ2には、ステップ1に指定した変数をすべて指定しておく必要があります。つまり、以下のようにモデルを指定します。
もし各ステップにそれ以前のステップの変数が含まれていない場合、エラーが出ますので注意してください。この状態で「分析実行」を押すと、各ステップの結果と、階層的重回帰分析の要約の結果が出力されます。各ステップは普通の回帰分析と同じ出力なので、ここでは階層的重回帰分析の結果、"HRA"について説明します。
モデル比較のところでは、各ステップのR2と、R2の変化量、その有意性検定などの結果が出力されます。また、AICやBICといった情報量基準も出力されます。これらを参考にして、メインの説明変数の説明力を検討しましょう。
また、非標準化係数とあるところには、各ステップの要約した結果を載せています。標準化係数やVIF、偏η2などの指標は各ステップのシートに出力しているので、そちらを参照してください。
◆回帰分析の交互作用効果の検討
回帰分析を使って交互作用効果を検討する利点や、数学的な話は比治山大学の前田先生のHPを参照してみてください。非常に詳しく丁寧に書いてありますので、参考になります。
ここでは、HADを使って回帰分析の交互作用を検討する方法を書きます。
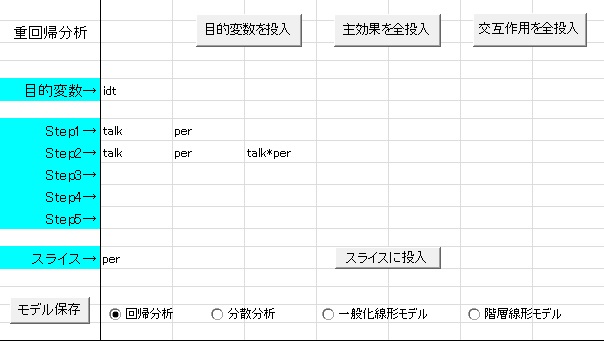
まず回帰分析のモデリングスペースを開いた状態で、上と同じように目的変数を指定します。次に、例えばtalkとperの主効果と、その二つの交互作用効果を検討したいとすると、以下のように指定します。
入力のポイントは、
- 交互作用項は掛け算(*)でつないで入力する
- 交互作用項は、主効果の次のステップに入力する
- スライス変数(群分けをする変数)を指定する
の3つです。
1.は、上の図のようにtalk*perといった感じで*で変数をつなぎます。
あるいは、「交互作用を全投入」ボタンを押すと、使用変数に指定した変数間すべての交互作用項を自動で投入します。
※ただし、ステップ5までしか入力できません。
また、特定の変数のみ交互作用を見たい場合は、交互作用を見たい変数を選択した状態で、Ctrlキーを押して「交互作用を全投入」ボタンを押してください。すると、選択した変数だけ交互作用項が入力されます。
2.は、交互作用効果は主効果を統制したうえでの効果として検討する必要があるため、主効果の次のステップに入力するのがセオリーです。
3.は、単純効果分析をするために必要な指定です。単純効果を見る場合、ある変数の高群・低群の効果を検討する必要があるのでそのような群分け変数(HADではスライス変数と呼びます)を指定します。
例では、perつまり課題のパフォーマンスが高いときと低いときで、talkつまり発言量の効果が変わるという予測を検討するモデルになっています。
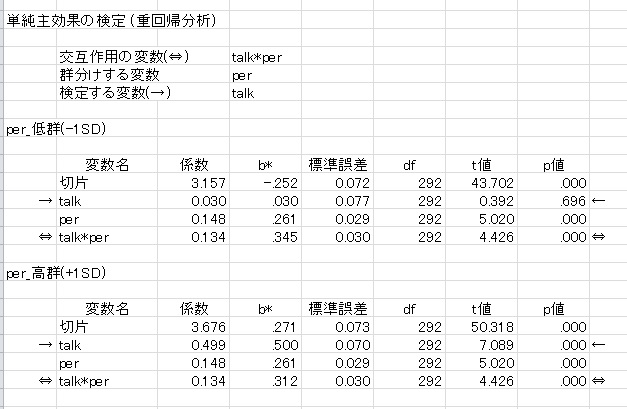
この状態で「分析実行」を押すと、各ステップの結果、階層的重回帰分析の要約("HRA")、そして単純効果分析の結果("slice")が出力されます。ここでは、"slice"の結果について説明します。
回帰分析の単純効果は、スライス変数の+1SDと-1SDのポイントでの単純効果を検討するのが一般的です。HADでもそれにならって、±1SDでスライスします。
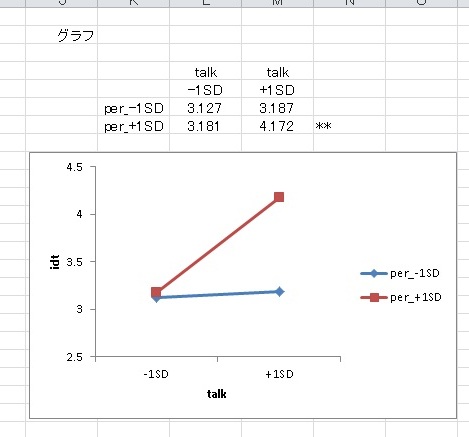
この例では、per低群ではtalkの効果が非有意ですが、per高群では、高度に有意になっています。また、グラフも表示されます。
今回の例では2要因の交互作用でしたが、HADでは3要因まで検討することができます。
その場合は、スライス変数を2つ指定する必要がありますので、別々のセルに指定してください。
以上が回帰分析で交互作用を検討する方法でした。