t検定(二つの平均値の差の検定)は今まで分散分析のプロシージャで走らせていましたが、ver9.5からは「分析」ボタンから簡単にできるようになりました。
ここではその簡単版のやり方を説明します。
また、順位の差の検定であるノンパラ検定の方法もほぼ同じなので、触れておきます。
続きを参照してください。
まずは、データの説明から。以下のようなデータを例に使います。
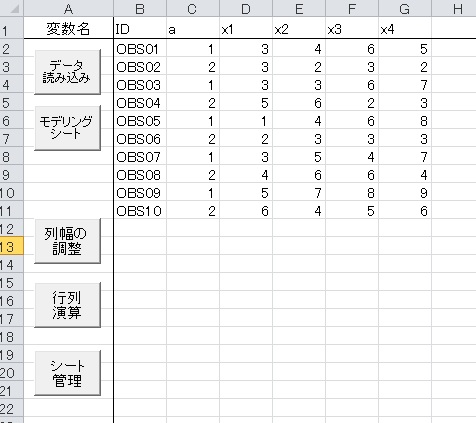
このデータを「データ読み込み」で読み込んで、モデリングシートに移動します。
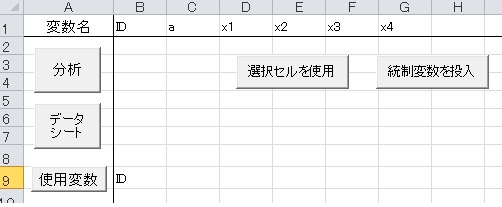
ここから分析が始まるのですが、t検定には対応あるt検定と対応のないt検定があります。
対応のないt検定は、二つのグループの平均値の差を比較する方法です。
対応のあるt検定は、同じ人が答えた二つの変数の平均値を比較する方法です。
以下ではそれぞれの方法について説明します。
◆対応のないt検定
対応がない場合は、比較したい変数と、比較するグループを識別する群分け変数を指定する必要があります。今回の例では、aという変数でx4の差を検定したいとします。
その場合、目的となる変数x4を先に指定し、その後ろに群分け変数aを指定します。具体的には以下のようにします。

上の図のように、C列のセルにx4を、D列のセルにaを入力します。
覚え方としては、従属変数(目的変数)が先、独立変数(群分け変数)が後、です。
それでは「分析」ボタンを押してみましょう。以下のようなユーザーフォームが立ち上がります。
ここで、「平均値の差の検定」の「対応なし」を選択します。
この状態で「OK」ボタンを押せば、分析が実行されます。
以下のような結果が出力されます。

対応のないt検定では、通常のt検定の結果以外に、「Welch検定」の結果を出力します。Welch検定とは、各群の分散が等しくない場合、普通の方法ではt分布に従わないため、調整をする方法です。
従来では、等質性の検定(F検定など)を行い、有意だった場合にはWelch検定、そうでない場合には普通のt検定というのが常識でしたが、最近ではそうではないようです。それは、F検定→t検定が、検定の二重性の問題を持つという指摘があるからです。つまり、「F検定で有意だった場合だけWelchで、それ以外はt検定」という手続きを繰り返して実行すると、危険率を5%に抑えられない、ということです。
たとえば青木先生のページでは、常にWelchの検定を行う方が、タイプⅠエラーを犯す危険が最も低いことをシミュレーションで示しています。この結果は、F検定などせずに、常にWelch検定を採用することが妥当であることを示しています。また、Rのt.test関数はデフォルトがWelch検定で、普通のt検定はオプションで指定しないといけないようになっています。
これらを踏まえ、HADでは等質性の検定は行わず、デフォルトでWelch検定をそのまま載せています。同時に、等分散を仮定するt検定結果も出力しています(ただしエラーバーは等分散を仮定しない標準誤差に基づく)。とはいえ、Welch検定はあくまで「近似」であるため、絶対に分散が等質だという確信が何らかの理由であるなら、t検定を採用してもいいでしょう。
また、ver9.5から、差についての効果量を出力するようにしました。「r」とあるのがそれです。
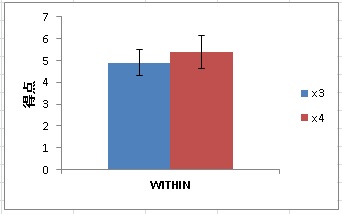
この表の隣には、以下のようなグラフが出力されます。
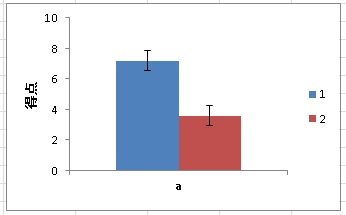
エラーバーはデフォルトで表示されますが、上向きだけにしたい、消したい、という人はエクセルのグラフなので簡単に編集できます。
また、対応のないt検定の場合、群分け変数の値にラベルをつけたい、という人もいると思います。その場合は、モデリングシートに戻って、変数情報を変更することで値ラベルの設定ができます。
変数情報の隣にある、「フィルタ」「値」「ラベル」のボタンのうち、「値」ボタンをクリックします。
すると、以下のようなユーザーフォームが立ち上がります。
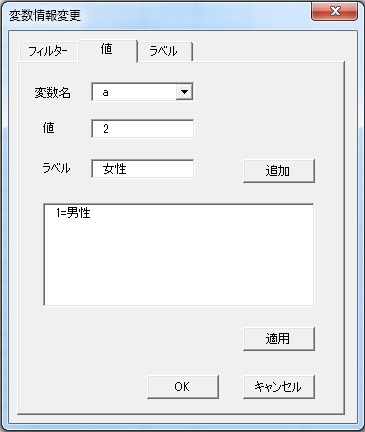
ここで、上の図のように1を男性、2を女性といったように、値ごとにラベルを設定できます。
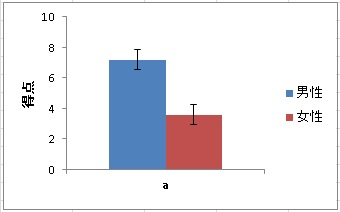
すると、以下のように結果やグラフに反映されます。
◆対応のあるt検定
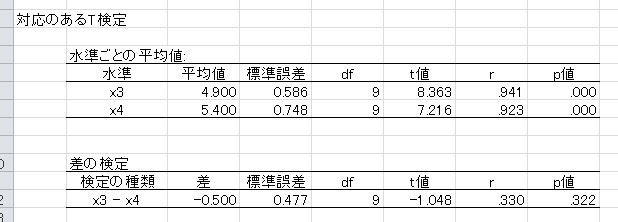
対応のあるt検定では、比較する二つの変数を指定する必要があります。
今回はx3とx4を比較することにします。
以下のように入力します。
その後、分析ボタンを押して、今度は「対応あり」をチェックします。
グラフの「WITHIN」というのは、HADが自動的につけた参加者内要因の名前です。
◆一要因分散分析も可能
実は「分析」ボタンから実行できるのはt検定だけではなく、分散分析も可能です。ただし、1要因に限ります。
例えば、x1,x2,x3,x4の4つの平均値を比較したい場合は、使用変数に4つとも指定することで分析可能です。その場合は、1要因参加者内計画(4水準)になります。
また、対応のない場合でも、3グループ以上の差の検定を行うことができます。
加えて、多重比較も実行可能です。
分散分析の結果の見方については、分散分析のやり方のほうを参照してください。
◆母集団の分布を仮定しない検定(ノンパラメトリック検定)
さて、次にノンパラメトリック検定(ノンパラ検定)の方法を説明しておきます。
ノンパラ検定とは、母集団の分布を仮定しない検定の方法です。例えば順序尺度で得たデータの場合、2群の順位に違いがあるかどうかを検定したいこともあるでしょう。
そういった場合、順位は基本的に正規分布しないので、母集団の正規性を仮定するt検定を使うことができません。
ノンパラ検定は、そのような、正規性から逸脱したようなデータを扱うための方法です。
HADには順位の差の検定も可能です。一般的によく使われる方法は以下の4つです。
- 2つの対応の「ない」順位の差の検定:マンホイットニーの検定
- 2つの対応の「ある」順位の差の検定:ウィルコクソンの符号和検定
- 3つ以上の対応の「ない」順位の差の検定:クラスカル・ウォリスの検定
- 3つ以上の対応の「ある」順位の差の検定:フリードマンの検定
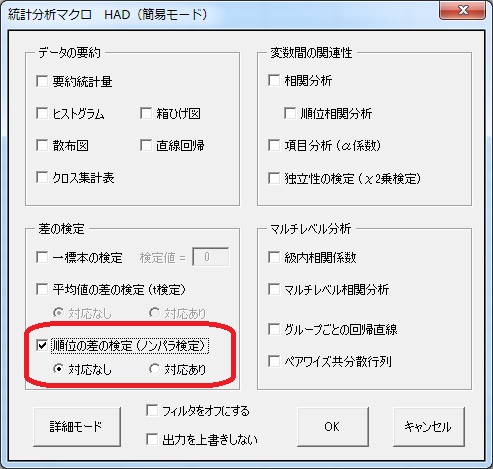
具体的な方法は、t検定の時とほとんど同じです。「分析」ボタンを押した後、以下の「順位の差の検定」を選択すればOKです(カテゴリカル分析のところにあります)。
3水準以上の場合は、多重比較(Siegel & Castellanの方法)も行います。