カテゴリカル因子分析について

今回は、それの応用編でカテゴリカル因子分析について書きます。事前に、カテゴリカルデータの相関係数についての記事を読んでもらった方がわかりやすいと思います。

さて，ここでいうカテゴリカルデータとは、順序性を持ったもの、つまり大小関係はあるけど間隔は等しいとは限らない、というデータをさすことにします。名義尺度は対象ではありません。

順序性を持ったカテゴリカルデータは、得られたデータは順序尺度だけどその背景には連続性を持った変量があると仮定されることが多いです。

例えば100メートル走の順位だってそうです。金メダルの人は銀メダルより足が速いことしかわかりませんが、ちゃんと測ればどれくらい早いか、つまり連続的な「足の速さ」というパラメーターを知ることができるでしょう。

心理学の場合、「ちゃんと測れば」というのが難しいので、統計的な推定によって順序尺度からその背景にある連続的なパラメーターを推定するという作業が必要になってきます。

その作業が今からお話しするカテゴリカル因子分析です。

カテゴリカル因子分析は、順序尺度で測定された項目群から、その背景にある連続的な変量を推定する方法です。順序尺度項目が一つだけだとお手上げですが、それがいろんな角度から測定したものが複数あれば、より正確に推定することができます。興味ある人は、続きをどうぞ。

カテゴリカル因子分析の利点

カテゴリカル因子分析を使うメリットは、大きく分けて３つあります。

順序尺度で測定された変数から、因子負荷量をより正確に推定し、背景にある連続的なパラメータも正確に推定できる。
項目間の相関だけでなく、項目の難しさ（つまりは得点の高さ）も考慮に入れて推定する。
天井効果や床効果が出てしまったデータ、打ち切りデータなどからも、ある程度正規性を持ったパラメータを推定できる

順序尺度によって測定されたデータの短所は、結局のところ１．連続的なものを間隔を無視して荒く測定している、２．最低点と最高点が設定される、という点にあります。これらの限界を、カテゴリカル因子分析はある程度是正してくれます。

つまり、尺度でとったデータが荒かったり、最高点や最低点に偏ってしまった場合に、役立つ方法だといえます。

カテゴリカル因子分析の方法

カテゴリカル因子分析には、いくつかの方法があります。代表的なのは以下の3つです。

ロジスティック関数を利用して、最尤法で推定する方法
ポリコリック相関係数を利用して、重みつき最小二乗法（WLS）で推定する方法
ベイズ統計学に基づいて、MCMC法で推定する方法

１．は項目反応理論などが利用している方法です。項目反応理論についてはGoogleで調べるといろんな資料がでてきますので、詳しいことは省略します。小杉先生の資料は比較的わかりやすいと思います。簡単に言えば、ロジスティック回帰分析の因子分析版だと思ってもらえたらいいと思います。ロジスティック関数を使うモデルは、項目の数や順序段階の数が多いと非常に計算量が増えるため、少数の項目でしか分析できないというデメリットがあります。

２．は、カテゴリカルデータの相関係数の記事で説明した、ポリコリック相関係数を使って因子分析をする方法です。ただし、そのままポリコリック相関係数を使うのではなく、標準誤差で重みづけた最小二乗法で推定します。この方法はデータの規模が大きくても推定はそれほど時間がかからないのが利点です。ただし、二段階で推定しているので、推定の精度は落ちるかもしれません。

３．はベイズ統計学に基づくMCMC法（マルコフ連鎖モンテカルロ法）を使って推定する方法です。最近ではAmosやMplusなどのソフトウェアもベイズを使えるようになったので、比較的手が届きやすくなっています。1や2に比べて仮定が少なく推定ができるため、使いやすい方法だといえます。ただ、収束までに時間がかかることと、ベイズ統計という新しい方法ゆえのとっつきにくさがデメリットかもしれません。それらも、統計やコンピューターが発展すればなくなっていくものだと思いますが。

さて、3つの方法を紹介しましたが、得られる推定結果はほとんど同じです。なのでどれを使っても問題はないです。使いやすい環境のものを使うといいでしょう。

カテゴリカル因子分析の実際

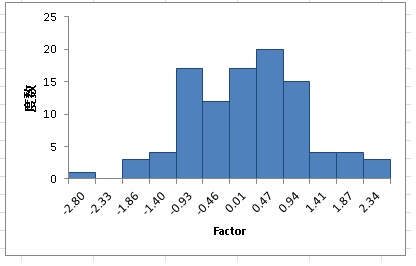
それでは、試しにダミーデータを使ってカテゴリカル因子分析の長所などを見ていきましょう。今回は、10項目の5件法尺度で、ある心理変数を推定することを考えます。まず、正規乱数を利用して100人のデータを発生させました。これが心理変数の真の値だとします。正規乱数なので、正規分布に近いデータになっています。

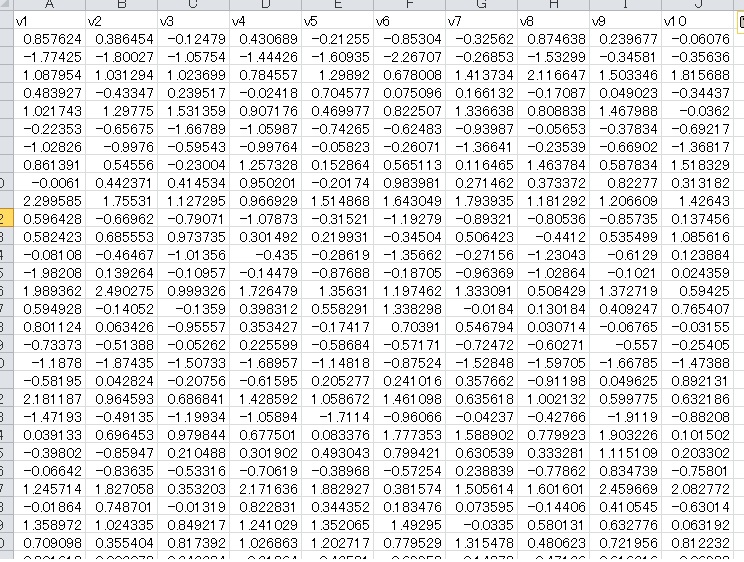
この変数を測定するために、10個の側面があるとします。それらはすべて相関が0.7ぐらいになるように乱数を発生させます。以下のようなデータです。

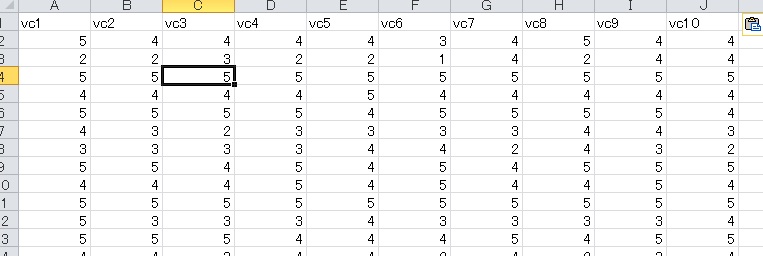
しかし、実際には10項目の尺度得点はこのように連続的には得られません。そこで、5段階になるように変換しました。

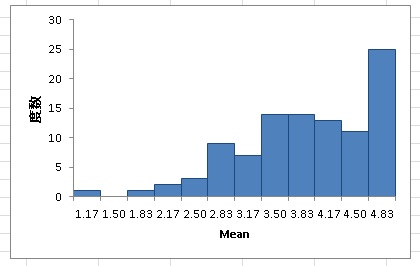
このとき、カテゴリカル因子分析の利点を強調するために、天井効果が出てしまったデータを想定して、得点が高い方に偏るように変換しました。10項目の尺度平均値の分布が下の図のようになりました。

完全に天井効果が出ています。これでは、尺度得点を使って検定することなどが難しくなってしまいます。そこでカテゴリカル因子分析を使って、どのように推定されるか見てみましょう。ソフトウェアはMplus6.12を使って推定しました。

まず、真の共通性と、普通に因子分析（最尤法）で推定した共通性、そしてカテゴリカル因子分析の共通性を見てみましょう。なおカテゴリカル因子分析はロジスティックモデルで推定しました。

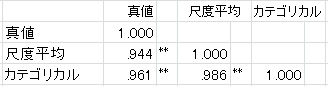
見て分かるように、カテゴリカル因子分析のほうが正確に推定できています。とはいえ、5件法ぐらいだと、普通の方法でもそれなりにうまく推定ができているようです。次に、因子得点を推定してみました。元のデータとの相関を見てみましょう。

若干ではありますが、真値との相関が高くなっています。また、因子得点の分布は以下のような感じになります。

尺度得点に比べて、かなり分布が是正されているのがわかります。このように、カテゴリカル因子分析は真値をより正確に推定し、天井効果があるようなデータでも正規分布に近くなるように推定してくれます。

ただ、今回の例を見てもわかるように、5件法ぐらいなら結構正確に推定できているのがわかると思います。なので、順序尺度だからといってそんなに神経質になる必要もありません。

例えば2件法のデータだったり、天井効果が顕著にでてしまったり、得点の間隔がどう考えても等しくない、といった場合には有効だと思います。そうでない限りは普通に因子分析をしても問題ないでしょう。

また、カテゴリカル因子分析も万能ではないので、なんでもかんでもうまく推定してくれるとは限りません。元のデータがあまりに正規分布から外れているなら、もしかしたら真のパラメーターも正規分布ではないかもしれません。そのようなデータに対して、背後に正規分布を仮定するカテゴリカル因子分析を利用するのは、もしかしたら誤りである可能性もあります。

ソフトウェア

カテゴリカル因子分析が実行できるソフトウェアを紹介します。

今回使ったMplusが個人的には最もお勧めです。なぜなら、ロジスティックモデルと重みつき最小二乗法、そしてベイズ推定のすべてを実行することができるからです。また、重みつき最小二乗法なら探索的因子分析も可能で、回転もできます（Mplus7からはベイズでも可能のようです）。また、因子分析だけでなく、SEMに応用することもできるため、非常に汎用性が高いです。

Amos（7以降）もベイズ推定が可能ですが、探索的因子分析ができません。複数の因子がある場合は検証的因子分析の方法を使う必要があります。

Rは1因子なら、項目反応理論のパッケージ（ltmパッケージ）の中にある関数やベイズ因子分析（MCMCfactanal関数)を使って実行ができます。複数因子となると、今のところスムーズにやってくれるのは知りません（きっとどこかにはあると思いますが）。

あと，HADでも重み付き最小二乗法を使ったカテゴリカル因子分析が可能です。

そのほか、項目反応理論のソフトウェア（例えば、EasyEstimationやExametrika)も可能ですが、これらも1因子にしか対応していません。また、項目反応理論で得られる推定値は、正確には因子負荷量ではないため、変換する必要があります。そのあたりの面倒さも考えると、あまりお勧めしません。

このように、カテゴリカル因子分析が実行できるソフトは多いですが、多因子に対応しているものは少ないです。完全に対応しているのはMplusぐらいじゃないでしょうか。HADも部分的には可能です。

1因子のデータ、あるいは検証的因子分析でも大丈夫ということならAmos（7以降）でベイズ推定を使えば比較的簡単に実行できるのでお勧めです。

Mplusでカテゴリカル因子分析を実行するためのコード

一応、Mplusでカテゴリカル因子分析を実行するためのコードを書いておきます。今回のダミーデータの分析に使ったコードです。

ロジスティックモデルか重みつき最小二乗法を使う場合のコード

DATA: FILE IS "test.txt"; !データファイルはimpファイルと同じ場所に置く

VARIABLE: NAMES ARE v1-v10; USEVARIABLES ARE v1-v10; CATEGORICAL ARE v1-v10; !この文がカテゴリカルデータを指定するところ

ANALYSIS: TYPE IS GENERAL; ESTIMATOR IS MLR; !最小二乗法の場合は、WLSMVと書く

MODEL: f1 by v1-v10*; f1@1;

OUTPUT:stand(stdyx) sampstat; !標準化された結果を参照するためにSTAND（STDYX)を書く

Savedata: save = fscores; !因子得点を推定し、ファイルに保存するためのコード File is factor_score.txt; !ファイル名は任意

次に、ベイズ推定を使う場合のコード

DATA: FILE IS "test.txt"; VARIABLE: NAMES ARE v1-v10; USEVARIABLES ARE v1-v10; CATEGORICAL ARE v1-v10;

ANALYSIS: TYPE IS GENERAL; ESTIMATOR IS BAYES; FBITERATIONS = 20000; Process = 3; Chain = 5; Thin = 2;

MODEL: f1 by v1-v10*; f1@1;

OUTPUT:stand(stdyx) sampstat;

PLOT: TYPE=PLOT2;

Data Imputation: ndatasets = 100; plausible = factor_score.txt; !ベイズの場合は因子得点の保存は上のように書く

※FBITERATIONSは、リサンプリングの数 ※Processは使用するCPUコアの数。4つあるなら3つぐらいがお勧め

以上です。