[R]　Rで重回帰分析で交互作用を検討する方法(pequodパッケージ)

普段は自作の統計プログラムHADを使って分析していますが，人にいろいろ教えるときにはRも使っている清水です。

さて，今回はRで重回帰分析で交互作用を検討する方法について解説します。

昔，Rで重回帰分析で交互作用を検討するためのコードをアップしていたのですが，最近はもっと便利にできるパッケージがあるようです。というか僕が知らなかっただけか・・・

これについては，DARMという広大の院生・ポスドクが中心となってやっている勉強会のページで知りました（ここ）。まぁネタぱくってる，っていう話なんですけど（笑）。ぜひDARMのページも見てやってください。

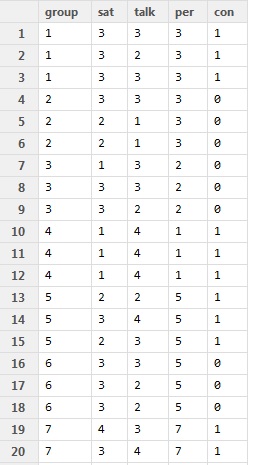
ここでは，次のようなサンプルデータを使います。20しか見えませんが，200人のデータです。サンプルデータはこちらからダウンロードできます。

これを”dat”に読み込みます。

dat <- read.csv("sampledata.csv")

まずは2要因の回帰分析を行ってみましょう。ここでは，従属変数はsat，独立変数はtalk，調整変数はperです。

で，使うパッケージはpequodです。そして，lmres関数を使います。

library(pequod)

model1 <- lmres(sat~talk*per, centered =c("talk", "per"), data =dat)
summary(mode1)

sat ~ talk*perというモデル式は，talkとperの主効果と，talkとperの交互作用を投入する，という意味です。つまり，sat~talk+per+talk:perと同じ意味です。

次に，centered=では，中心化する（平均を0にする）変数を指定します。変数名を""でくくるのを忘れずに。基本的に，回帰分析の交互作用を検討する場合，平均を0にします。それは，多重共線性を避けるためです。

結果は次のようになります。

talk xx perの項が有意であることに注目しましょう。交互作用項が有意だったので，単純主効果を検討しましょう。

単純主効果は，以下のコードで検討します。

model2 <- simpleSlope(model1, pred="talk", mod1 = "per")
summary(model2)

simpleSlopeの二つ目のＳが大文字なのに注意。predは予測変数，つまり独立変数を指定します。つまり，talkがそれになります。mod1は，調整変数の一つ目，ということで，perを指定します。結果は以下のようになります。

perが高群（+1SD)の場合に，talkの効果は有意ですが，低群(-1SD)の場合，非有意であることがわかります。

次に，単純効果をグラフ表示したい場合には，PlotSlope関数を使います。

PlotSlope(model2)

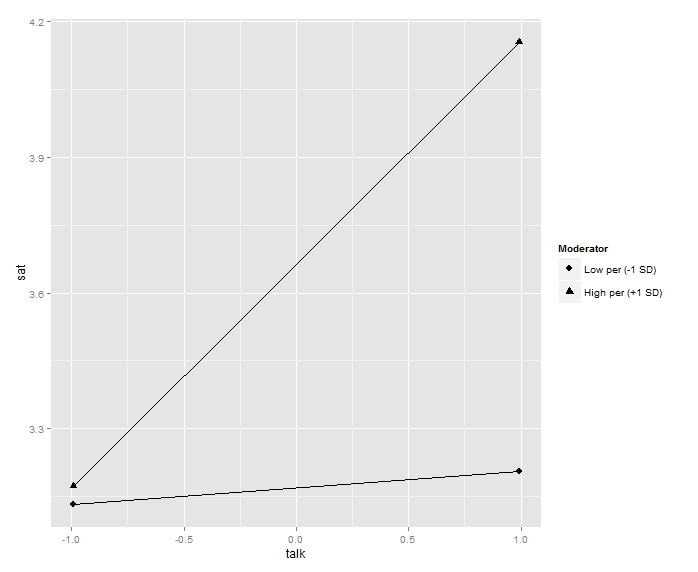
大文字，小文字の違いに注意。これを走らせると，以下のようなグラフが表示されます。

なかなかいい感じですね。

なお，このlmres関数では，交互作用項が二つ以上でも単純主効果の分析ができます。たとえば，下のように3要因の重回帰分析を実行した場合，

model1 <- lmres(sat~talk*per*con,centered=c("talk","per","con"),data=dat)

結果は以下のようになります。

単純効果の検定も，2要因の時と同様に，

model2 <- simpleSlope(model1,pred="talk",mod1 = "per",mod2="con")

と書きます。ご丁寧に，ボンフェローニの修正p値も出力します。

また，出力したモデルのF_changeという要素を見れば，階層的重回帰分析の要領で，交互作用ごとのΔR2乗値が確認できます。

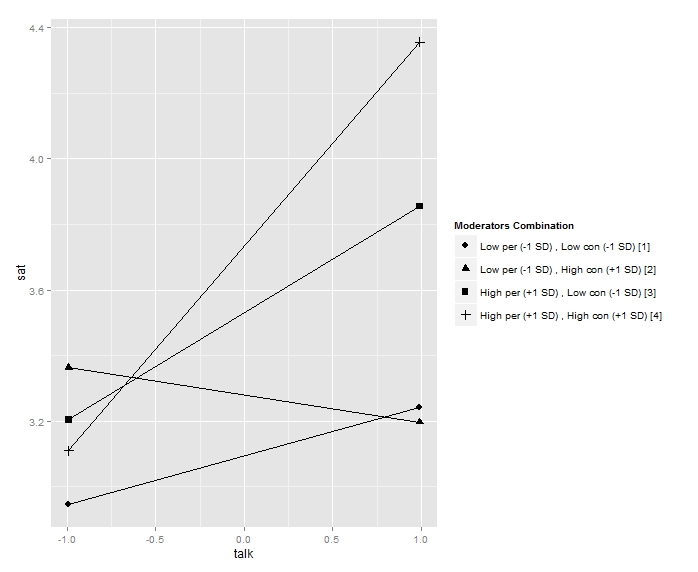
グラフは下のようになりました。

すべての群が同じグラフに表示されるのは，便利なのか見にくいのかは評価が分かれるところですが，Rでここまで簡単に重回帰の交互作用を検討できるパッケージがあるのはとても便利ですね。