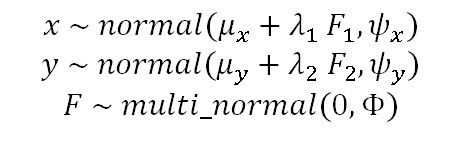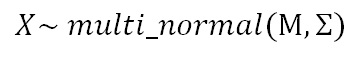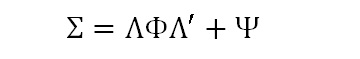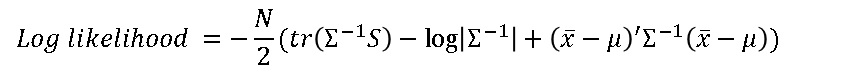この記事は、Stan advent calendarの16日目の記事です。
Stan楽しんでますか?楽しいですね。今回は構造方程式モデリングをベイズ推定するぞ☆という話です。
潜在変数を推定する
さて、僕は心理学を専門としているのですが、心理学では心を潜在変数としてい推定する、ということをやります。よく心理尺度とかで、「私は~だと思う」という質問に「あてはまる」「あてはまらない」とかいう回答を選択させるやつありますよね。あれは、ひとつの項目で何か心がわかると思って使ってるわけじゃないのです。複数の項目に答えてもらって、その共通要素を推定しようとしています。
心理学では、心の状態→行動という仮定をおくので、もしよく似た複数の質問に対して一貫した意見を回答しているならば、そこには目に見えない心の状態(たとえば社会的態度)を持っていると仮定して、その得点を推定したりするのです。これを可能にする方法として因子分析とか構造方程式モデリングとかが考案されています。
構造方程式モデリングとは・・・確認的因子分析を例に
今回はタイトルにあるように、構造方程式モデリングをStanでやりたいわけですが、構造方程式モデリングについて簡単に説明します。
一番簡単な構造方程式モデリングは、確認的因子分析と呼ばれる方法です。
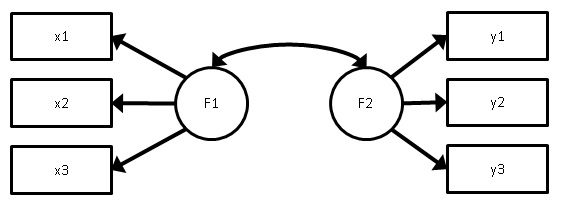
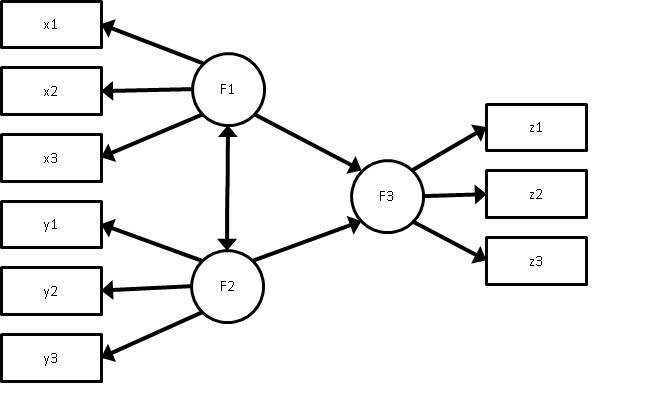
上の図のように、観測変数x1~x3、y1~y3で測定された潜在変数F1、F2を推定して、またその潜在変数同士の相関も推定するというモデルです。以降、観測変数を項目、潜在変数を因子と呼びます。どの項目がどの因子を測定しているかが決まってるので、確認的因子分析と呼ばれます。
確認的因子分析の確率モデルは、各項目が正規分布に従い、さらに因子F1、F2が標準多変量正規分布に従うことを仮定します。
このとき、μは平均、λは因子負荷量、ψは項目の誤差分散、Φは因子の共分散(相関)行列です。
さて、構造方程式モデリングは、一般的なモデリングを行うため、に因子得点を直接推定せず、積分消去します。すると、確率モデルは観測変数の多変量正規分布になります。
大文字のXは項目x1~x3と項目y1~y3を全部含んだ観測変数全部だと思ってください。またΜは平均値μを要素として持つ平均ベクトルで、Σは、観測変数である各項目の「モデル上での共分散行列」です。
そして、モデル上での共分散行列を上記のパラメータで表現しなおすと次のようになります。
ここで、Λは因子負荷行列(λを行列に並べたもの)、Φは因子間相関行列、Ψは誤差分散を対角項においた対角行列です。このように、共分散行列を因子負荷量、誤差分散、因子間相関というパラメータで表現したものを共分散構造と呼びます。構造方程式モデリングがもともと共分散構造分析と呼ばれたのは、ここからきているわけです。
Stanで確認的因子分析
これをStanで書いてみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
data{ int N; //サンプルサイズ int P; //変数の数 int L; //潜在変数の数 int M; //因子負荷量の数 int Linput[P,L]; vector[P] x[N]; } parameters{ vector[P] mu; vector[M] lambda; corr_matrix[L] phi; vector } transformed parameters{ matrix[P,L] Lambda; matrix[P,P] Psy; cov_matrix[P] Sigma; { int k; k = 0; Lambda = rep_matrix(0,P,L); for(i in 1:P){ for(j in 1:L){ if(Linput[i,j]==999){ k = k + 1; Lambda[i,j] = lambda[k]; } } } } Psy = diag_matrix(psy); Sigma = Lambda*phi*Lambda' + Psy; } model{ x ~ multi_normal(mu,Sigma); mu ~ normal(0,10^2); lambda ~ normal(0,10^2); phi ~ lkj_corr(1); psy ~ cauchy(0,2.5); } |
ここで注意が必要なのは、潜在変数を使うモデルでは、因子得点の符号について不定性があります。なので、初期値を与えずに普通に推定すると、因子負荷量があるチェインは正に、別のチェインは負に推定されて、事後分布が双峰になってしまいます。
よって、まずは最尤法か何かで因子負荷量を推定して、その符号に合わせて初期値を1、‐1とかでもいいのでいれておくと安定します。
あと、Linputというのは、因子負荷行列のなかでどれが自由パラメータ(推定する因子負荷量)かを識別するためのものです。項目数×潜在因子数の行列を入れます。ここでは、自由パラメータの場合は999、推定しない場合は0を入力しています。
Rコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
library(rstan) library(psych) library(MASS) N <- 200 Sig <- matrix(c(1,0.5,0.5,1),nrow=2,ncol=2) f <- mvrnorm(100,c(0,0),Sig) x <- f[,1] y <- f[,2] x1 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) x2 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) x3 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) y1 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) y2 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) y3 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) dat <- data.frame(x1,x2,x3,y1,y2,y3) modelcfa <- stan_model("cfa.stan") P <- ncol(dat) L <- 2 Linput <- c(999,999,999,0,0,0,0,0,0,999,999,999) Linput <- matrix(Linput,nrow=P,ncol=L) lambdainit <- list(lambda=c(1,1,1,1,1,1)) initcfa <- list(lambdainit,lambdainit,lambdainit,lambdainit) datacfa <- list(N=nrow(dat),P=P,L=L,M=length(which(Linput==999)),x=dat) fit.cfa <- sampling(modelcfa,data=datacfa,init=initcfa) print(fit.cfa,pars=c("lambda","phi","psy")) |
真値は、因子間相関が0.5、因子負荷量が全部0.8のモデルです。Nは200です。
結果はこんな感じでうまく推定されました。lambdaが因子負荷量、phiが因子間相関行列、psyが各変数の誤差分散です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat lambda[1] 0.86 0 0.07 0.74 0.81 0.86 0.90 0.99 3234 1 lambda[2] 0.87 0 0.06 0.75 0.83 0.87 0.92 1.00 2744 1 lambda[3] 0.92 0 0.07 0.79 0.88 0.92 0.96 1.06 3051 1 lambda[4] 0.74 0 0.06 0.62 0.70 0.73 0.78 0.86 3254 1 lambda[5] 0.79 0 0.07 0.67 0.75 0.79 0.83 0.93 3171 1 lambda[6] 0.80 0 0.06 0.68 0.76 0.80 0.84 0.92 3001 1 phi[1,1] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 4000 NaN phi[1,2] 0.44 0 0.07 0.30 0.39 0.44 0.49 0.56 4000 1 phi[2,1] 0.44 0 0.07 0.30 0.39 0.44 0.49 0.56 4000 1 phi[2,2] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 3457 1 psy[1] 0.41 0 0.06 0.30 0.37 0.41 0.45 0.53 3335 1 psy[2] 0.33 0 0.05 0.23 0.29 0.33 0.37 0.44 3521 1 psy[3] 0.38 0 0.06 0.26 0.34 0.38 0.42 0.51 3354 1 psy[4] 0.37 0 0.05 0.27 0.33 0.36 0.40 0.47 3687 1 psy[5] 0.42 0 0.06 0.31 0.38 0.42 0.46 0.55 4000 1 psy[6] 0.26 0 0.05 0.17 0.23 0.26 0.30 0.37 2886 1 |
因子間の因果関係を考える
構造方程式モデルは、観測変数だけでなく、因子同士の因果関係も推定できます。例えば次のようなモデルです。
このようなモデルでも、観測変数について多変量正規分布を仮定する点は同じです。つまり、
です。しかし、一般的な構造方程式モデリングの場合、平均構造および共分散構造は次のようになります(なお、ここではRAM形式で書いてます)。
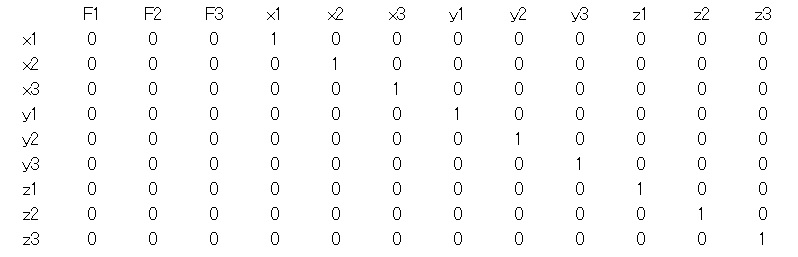
ここで、Gは因子と項目を識別するための選択行列で、項目数×(項目数+因子数)の行列で、左側から因子数分の列ベクトルはすべて要素が0で、残りは単位行列であるような行列です。次のような感じの行列です。
Iは単位行列、Λはパスおよび因子負荷量を表す影響力行列、Ψは分散と共分散を含むパラメータを行列にしたものです。A(alphaの大文字)は切片パラメータベクトルです。
ただし、今回のモデルを識別させるためには、因子の尺度の不定性を回避するために、因子の分散を1に固定するか、各因子の因子負荷量を1つだけ1に固定するかのどちらかの制約を与える必要があります。ここではx1、y1、z1の因子負荷量を1に固定するにします。
これをStanで書いてみましょう。
ただし、今回もいろいろ外部から推定するパラメータかどうかを識別するためのinputが必要なので、ちょっとStanコード的にはわかりづらくなっていると思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
data{ int N; //サンプルサイズ int P; //変数の数 int L; //潜在変数の数 int M; //影響力パラメータの数 int R; //共分散パラメータの数 int S; //分散パラメータの数 int A; //平均パラメータの数 int Linput[L+P,L+P]; int Pinput[L+P,L+P]; int Ainput[L+P]; vector[P] x[N]; } parameters{ vector[A] alpha; vector[M] lambda; vector[R] rho; vector } transformed parameters{ vector[P] Mu; cov_matrix[P] Sig; vector[L+P] Alpha; matrix[L+P,L+P] Lambda; matrix[L+P,L+P] Psy; Lambda = rep_matrix(0,L+P,L+P); Psy = rep_matrix(0,L+P,L+P); //parameter input { int k1;int k2;int k3;int k4; k1 = 0;k2 = 0;k3 = 0;k4 = 0; Lambda = rep_matrix(0,L+P,L+P); Psy = rep_matrix(0,L+P,L+P); for(i in 1:(L+P)){ if(Ainput[i]==999){ k4 = k4 + 1; Alpha[i] = alpha[k4]; }else{ Alpha[i] = Ainput[i]; } for(j in 1:(L+P)){ if(Linput[i,j]==999){ k1 = k1 + 1; Lambda[i,j] = lambda[k1]; }else{ Lambda[i,j] = Linput[i,j]; } if(Pinput[i,j]==999){ if(i==j){ k2 = k2 + 1; Psy[i,j] = psy[k2]; }else if(i k3 = k3 + 1; Psy[i,j] = rho[k3]; } }else{ Psy[i,j] = Pinput[i,j]; } } } } //covariance structure { matrix[P,L+P] G; matrix[L+P,L+P] T; G = append_col(rep_matrix(0,P,L),diag_matrix(rep_vector(1,P))); T = inverse(diag_matrix(rep_vector(1,L+P))-Lambda); Sig = G*T*Psy*T'*G'; Mu = G*T*alpha; } } model{ //model x ~ multi_normal(Mu,Sig); //prior alpha ~ normal(0,10^2); lambda ~ normal(0,10^2); psy ~ cauchy(0,5); rho ~ normal(0,10^2); } |
続いてRコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
library(rstan) library(psych) library(MASS) #data generating N <- 200 Sig <- matrix(c(1,0.5,0.5,1),nrow=2,ncol=2) f <- mvrnorm(100,c(0,0),Sig) x <- f[,1] y <- f[,2] z <- 0.5*x + 0.2*y + rnorm(N,0,0.5) x1 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) x2 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) x3 <- rnorm(N,0.8*x,(1-0.8^2)^0.5) y1 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) y2 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) y3 <- rnorm(N,0.8*y,(1-0.8^2)^0.5) z1 <- rnorm(N,0.8*z,(1-0.8^2)^0.5) z2 <- rnorm(N,0.8*z,(1-0.8^2)^0.5) z3 <- rnorm(N,0.8*z,(1-0.8^2)^0.5) dat <- data.frame(x1,x2,x3,y1,y2,y3,z1,z2,z3) #model setting P <- ncol(dat) L <- 3 #input matrix Linput <- read.csv("Linput.csv",header=F) Pinput <- read.csv("Pinput.csv",header=F) Ainput <- read.csv("Ainput.csv",header=F) #input M <- length(which(Linput==999)) S <- length(which(diag(as.matrix(Pinput))==999)) R <- (length(which(Pinput==999))-S)*0.5 A <- length(which(Ainput==999)) #data and initial values lambdainit <- list(lambda=c(0,0,1,1,1,1,1,1)) initsem <- list(lambdainit,lambdainit,lambdainit,lambdainit) datasem <- list(N=nrow(dat),P=P,L=L,M=M,S=S,R=R,A=A, Linput=Linput,Pinput=Pinput,Ainput=Ainput[,1],x=dat) #stanmodel compile modelsem <- stan_model("sem.stan") #sampling fit.sem <- sampling(modelsem,data=datasem,init=initsem) #output print(fit.sem,pars=c("lambda","rho","psy")) |
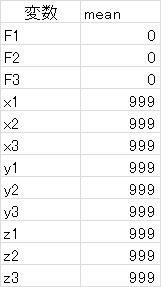
CFAと同様、自由パラメータか否かを識別するinputを用意します。今回も自由パラメータの場合は999をいれますが、固定パラメータの場合は固定したい数字を入れるようにしています。影響力を表す(いわゆるパス)行列はLinput、分散共分散を表す行列はPinputとしています。また、平均についてもAinputを用意いします。
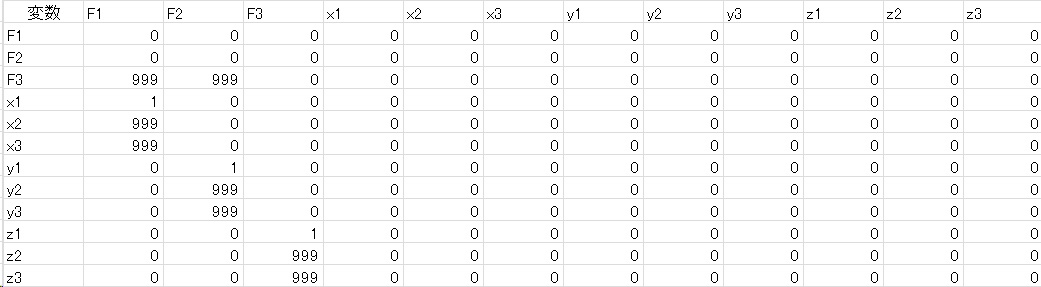
たとえばLinputは次ような感じになります。わかりやすさのために変数名を入れてますが、R上では数字のところだけを入力します。csvファイルでいれても、クリップボードから入れてもいいと思います。
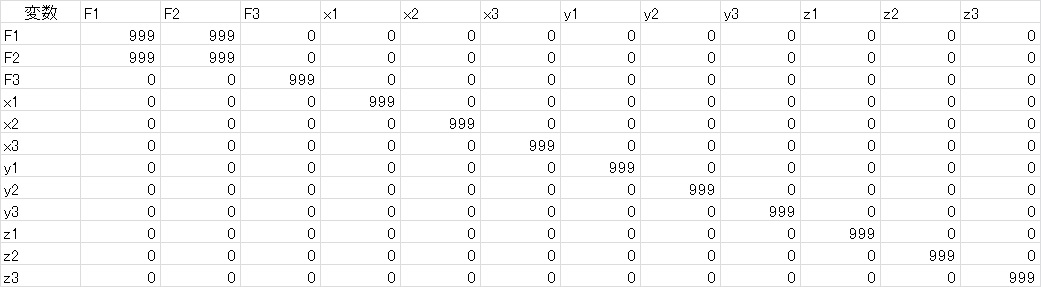
つぎにPinputです。
最後にAinput。
結果は次のような感じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat lambda[1] 0.44 0 0.07 0.31 0.39 0.44 0.49 0.58 2014 1 lambda[2] 0.16 0 0.07 0.03 0.12 0.16 0.21 0.30 3361 1 lambda[3] 0.99 0 0.10 0.80 0.92 0.98 1.05 1.18 2190 1 lambda[4] 0.97 0 0.09 0.80 0.90 0.96 1.03 1.16 1992 1 lambda[5] 1.10 0 0.11 0.91 1.03 1.10 1.18 1.33 1857 1 lambda[6] 1.15 0 0.11 0.94 1.07 1.14 1.22 1.38 1718 1 lambda[7] 1.17 0 0.14 0.92 1.08 1.16 1.26 1.47 1797 1 lambda[8] 0.96 0 0.12 0.75 0.88 0.96 1.04 1.21 1769 1 rho[1] 0.24 0 0.06 0.14 0.20 0.24 0.28 0.36 2238 1 psy[1] 0.67 0 0.11 0.47 0.59 0.66 0.74 0.90 2022 1 psy[2] 0.53 0 0.09 0.37 0.47 0.52 0.59 0.73 1801 1 psy[3] 0.17 0 0.04 0.11 0.15 0.17 0.20 0.26 2344 1 psy[4] 0.37 0 0.06 0.27 0.33 0.37 0.41 0.49 2821 1 psy[5] 0.47 0 0.06 0.36 0.43 0.47 0.51 0.61 3365 1 psy[6] 0.38 0 0.06 0.28 0.34 0.38 0.41 0.49 3431 1 psy[7] 0.35 0 0.05 0.26 0.32 0.35 0.39 0.46 2746 1 psy[8] 0.34 0 0.06 0.23 0.30 0.33 0.37 0.45 3037 1 psy[9] 0.39 0 0.06 0.27 0.35 0.38 0.43 0.51 2481 1 psy[10] 0.27 0 0.04 0.20 0.25 0.27 0.30 0.36 2481 1 psy[11] 0.39 0 0.06 0.28 0.35 0.39 0.43 0.51 3189 1 psy[12] 0.35 0 0.05 0.27 0.32 0.35 0.38 0.45 3039 1 |
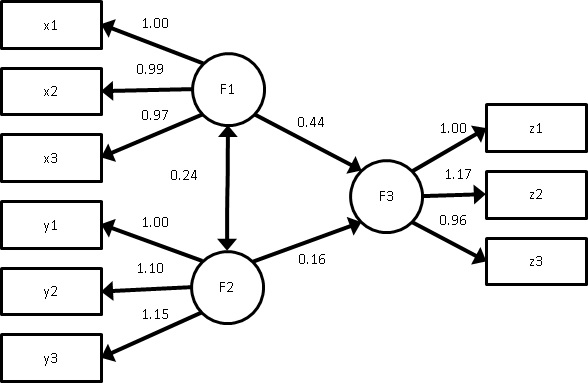
わかりづらいと思うので、パス図で書いてみました。
一応最尤法の結果を比較したら、ほとんど同じ結果でした。
さらなる一般化に向けて・・・おまけ
最後はかなり複雑な話なのでおまけレベルで見てもらえれば。
上のコードでもいくつか不十分な点があります。
1.共分散行列が正定値でなくなってサンプリングがとまる
2.母数の等値制約ができない
3.サンプルサイズが大きいと推定がすこぶる遅い
1番目。実は上のコードは少し複雑なモデルになると推定がうまくいかなくなります。それは、モデル上の共分散行列が正定値にならず、逆行列が求められなくなるからです。その原因の多くは、共分散がSDの積よりも大きく推定されてしまうことが問題であることが多いです。そこで、共分散を相関×SD1×SD2に分解して、相関係数が-1~1の範囲を超えないように推定すれば、この問題は解決します。
2番目。構造方程式モデルは自由なモデリングがウリですが、上のコードだとパラメータに等値制約をかけることができません。因子負荷量が全部等しいとか、そういうのができない、というわけです。そこで、自由パラメータを999としてましたが、同じパラメータは同じ数字、違うパラメータは違う数字を入れることで対処してみました。最初は1000から始まって、違うパラメータなら1001、1002と増えていき、同じパラメータは数字が1001で同じ、という感じです。どんどんinput行列の入力が面倒になりますね。
3番目。Stanの多変量正規分布の関数はすこぶる遅いので、サンプルサイズが大きい場合とても遅くなります。そこで、もし欠損値がなければ、構造方程式モデリングの尤度は十分統計量(ここでは平均と共分散行列)からでも計算できることを利用して、少しスピードアップを図ってみましょう。
まず、対数尤度は次の式で直接求まります。
ここで、Σはモデル上の共分散行列、μはモデル上の平均値、Sは標本共分散行列、xバーは標本平均値です。これをStan内で直接書いてtarget +=にいれてやれば、十分統計量だけからパラメータの推定ができます。よって、サンプルサイズが大きくてもほとんど推定時間には違いがなくなるというわけです(実際は値が大きくなるので時間は増えます)。
Stanコードは以下のようになります。Stanにしてはかなり長いですが、一回コンパイルしてしまえば、構造方程式モデルの範囲なら同じモデルが使いまわせるので、コンパイルレスになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
data{ int N; //サンプルサイズ int P; //変数の数 int L; //潜在変数の数 int M; //影響力パラメータの数 int R; //共分散パラメータの数 int S; //分散パラメータの数 int A; //平均パラメータの数 int M0; //ユニークな影響力パラメータの数 int R0; //ユニークな共分散パラメータの数 int S0; //ユニークな分散パラメータの数 int A0; //ユニークな平均パラメータの数 int Linput[L+P,L+P]; //影響力パラメータの入力 int Pinput[L+P,L+P]; //分散・共分散パラメータの入力 int Ainput[L+P]; //平均・切片パラメータの入力 vector[P] x[N]; //ローデータ matrix[P,P] Cov; //標本共分散行列 vector[P] Mean; //標本平均 } parameters{ vector[A0] alpha0; vector[M0] lambda0; vector vector } transformed parameters{ vector[P] Mu; cov_matrix[P] Sig; vector[A] alpha; vector[M] lambda; vector[R] rho; vector[S] psy; vector[L+P] Alpha; matrix[L+P,L+P] Lambda; matrix[L+P,L+P] Psy; //parameter input { int k1;int k2;int k3;int k4;real temp1;real temp2; k1 = 0;k2 = 0;k3 = 0;k4 = 0; for(i in 1:(L+P)){ if(Ainput[i]>=999){ k4 = k4 + 1; alpha[k4] = alpha0[Ainput[i]-999]; Alpha[i] = alpha[k4]; }else{ Alpha[i] = Ainput[i]; } for(j in 1:(L+P)){ if(Linput[i,j]>=999){ k1 = k1 + 1; lambda[k1] = lambda0[Linput[i,j]-999]; Lambda[i,j] = lambda[k1]; }else{ Lambda[i,j] = Linput[i,j]; } if(Pinput[i,j]>=999){ if(i==j){ k2 = k2 + 1; psy[k2] = psy0[Pinput[i,i]-999]^2; Psy[i,j] = psy[k2]; }else if(i if(Pinput[i,i]>=999){ temp1 = psy0[Pinput[i,i]-999]; }else{ temp1 = Pinput[i,i]; } if(Pinput[j,j]>=999){ temp2 = psy0[Pinput[j,j]-999]; }else{ temp2 = Pinput[j,j]; } k3 = k3 + 1; rho[k3] = rho0[Pinput[i,j]-999]*temp1*temp2; Psy[i,j] = rho[k3]; Psy[j,i] = rho[k3]; } }else{ Psy[i,j] = Pinput[i,j]; } } } } //covariance structure { matrix[P,L+P] G; matrix[L+P,L+P] T; G = append_col(rep_matrix(0,P,L),diag_matrix(rep_vector(1,P))); T = inverse(diag_matrix(rep_vector(1,L+P))-Lambda); Sig = G*T*Psy*T'*G'; Mu = G*T*Alpha; } } model{ //model { matrix[P,P] inv_Sig; inv_Sig = inverse(Sig); target += -N*0.5*(trace(inv_Sig*Cov)-log_determinant(inv_Sig)); target += -N*0.5*(Mean-Mu)'*inv_Sig*(Mean-Mu); } //prior alpha0 ~ normal(0,10^2); lambda0 ~ normal(0,10^2); psy0 ~ cauchy(0,5); rho0 ~ uniform(-1,1); } |
Rコードは以下です。データは先ほどと同じものを使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
P <- ncol(dat) L <- 3 #input matrix Linput <- read.csv("Linput.csv",header=F) Pinput <- read.csv("Pinput.csv",header=F) Ainput <- read.csv("Ainput.csv",header=F) #input M <- length(which(Linput>=999)) S <- length(which(diag(as.matrix(Pinput))>=999)) R <- (length(which(Pinput>=999))-S)*0.5 A <- length(which(Ainput>=999)) M0 <- length(unique(Linput[Linput>=999])) temp <- diag(as.matrix(Pinput)) S0 <- length(unique(temp[temp>=999])) temp <- Pinput[upper.tri(Pinput)==TRUE] R0 <- length(unique(temp[temp>=999])) A0 <- length(unique(Ainput[Ainput>=999])) #data and initial values lambdainit <- list(lambda0=c(0,0,1,1,1,1,1,1,1,1)) initsem2 <- list(lambdainit,lambdainit,lambdainit,lambdainit) datasem2 <- list(N=nrow(dat),P=P,L=L,M=M,S=S,R=R,A=A, M0=M0,S0=S0,R0=R0,A0=A0, Linput=Linput,Pinput=Pinput,Ainput=Ainput[,1], x=dat,Cov=cov(dat),Mean=apply(dat,2,mean)) #stanmodel compile modelsem2 <- stan_model("sem2.stan") #sampling fit.sem2 <- sampling(modelsem2,data=datasem2,init=initsem2) #output print(fit.sem2,pars=c("lambda","rho","psy","alpha")) |
さて、問題はinput行列を作るが恐ろしく面倒なのです。というわけで普通の利用にはあまり向かないと思うのですが、HADにもSEMの機能があるのでちょっといじってみました。その名もHAD2Stan_SEMです。
HADとはなんぞや?という人はこちらを見てください。
HADではパス図をかいて構造方程式モデルを実行できます。そこで、HADでパス図を描いてもらって、そこから自動的にStanにいれるようのinput行列を自動的に作る、というのをやってみたいと思います。
なお、HAD15.200以上のバージョンじゃないと対応してません。
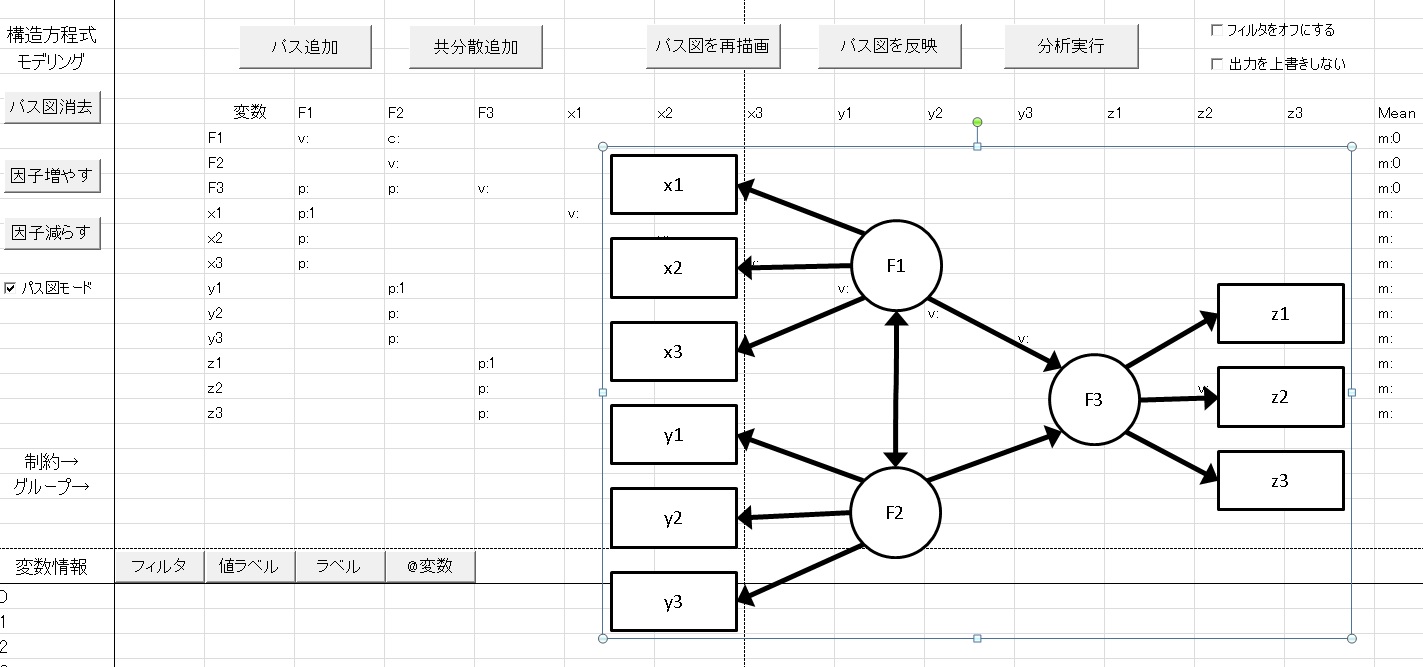
HADでの構造方程式モデリングの画面
HADでパス図を描いてモデルを作成したら、パス図モードを消します。すると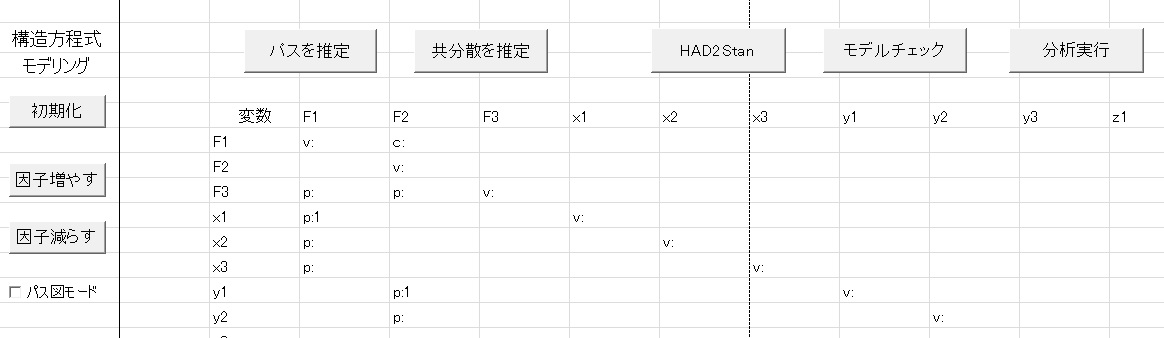
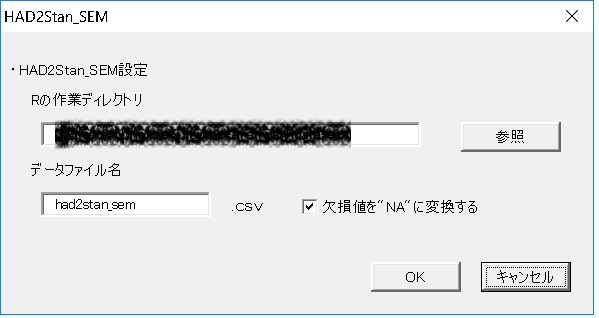
HAD2Stanというボタンが現れます。これを押すと、次のようなユーザーフォームがでます。ここに、Rの作業ディレクトリ(Rstudioを使ってる人なら、プロジェクトがあるフォルダ)を指定します。あと、データのファイル名も指定しておきます。
あとはOKを押すと、自動的にLinput.csv, Pinput.csv, Ainput.csv、そしてデータファイルが作業ディレクトリに保存されます。あとは、上のRコードを走らせれば、Stanが推定してくれるという仕組みです。
またStanで出力されたパラメータがどのパスなのかがわかりにくいと思います。そこで上のユーザーフォームでOKを押すと、次のようなシートが出力されてどのパラメータがモデルのどこに該当しているのかがすぐわかるようになります。
長くなりましたが、これである程度はStanで構造方程式モデリングが楽しめるかなと思います。
Enjoy, Stan!!