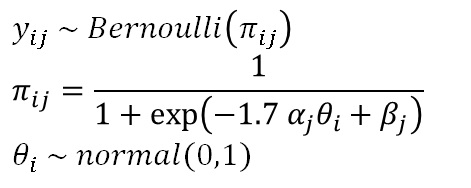この記事は、Stan advent calendar 2016の19日目の記事です。
今回は、多次元項目反応理論をStanでやってみたいと思います。
ちょっと今回は時間取れなくてやっつけです。すみません。
項目反応理論とは
項目反応理論(IRT)は、テストを評価するための数理モデルです。複数の項目について正解・不正解がデータで与えられたとき、そこから回答者の潜在的な学力などを推定する、そして問題の特徴も推定する方法です。
IRTの確率モデルは、以下のようになります。
ここで、yはある回答者i、項目jに対する回答で、正解なら1、不正解なら0が入力されたデータです。これが正答率πをパラメータに持つベルヌーイ分布から生成されたと考えます。
そして、正答率πは、ロジスティックモデルか正規累積モデルで表現されます。上では、ロジスティックモデルで書いてますが、1.7という係数は、正規累積モデルに近似するための係数です。IRTでは計算が簡単なこちらがよくつかわれます。
さて、πは項目についてのパラメータα、β、そして回答者についてのパラメータθによって構造化されます。αは識別力といい、項目がテスト全体に与える寄与で、βは閾値パラメータと呼ばれます。なお、普通のIRTでは、‐1.7α(θ-β)と構造化し、その場合のβは困難度パラメータと呼ばれますが、今回はStanに実装しやすいように(あと多次元IRTに対応するように)このようにしています。
最後に、θは標準正規分布に従うと仮定します。
これを多次元に拡張するには、いろいろごにょごにょあるんですが、ここは省略して、とりあえず潜在変数θが多変量正規分布から生成されると仮定するだけでOKとしておきます。ただし、探索的因子分析(山口大学小杉先生のStanアドカレ記事)と同様、多次元IRTでも識別力に制約を与えないと識別不定になります。よって、ここでも共分散行列のコレスキー分解した要素を使って、制約を与えます。
ただし、IRTの場合、データの生成メカニズムに正規分布を使っていないため、潜在変数を積分消去して多変量正規分布を確率モデルにする、という手が使えません。なのでここでは潜在変数も推定していきます。
Stanでの実装
今回は多次元IRTということで、θが多次元の場合のモデルを考えます。よって、確率モデルは複雑になりますが、基本は変わりません。あと、2値だけではなく、多値の順序反応尺度でも使えるように拡張してみました。順序尺度に対応した確率モデルには、Stanには順序ロジスティック分布というものが用意されています。詳細はマニュアルを見てください。これを使うととってもらくちんです。
Stanコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
data{ int N; //number of observations int P; //number of items int A; //number of factors int C; //scaling int y[N,P]; //data } transformed data{ vector[A] mu_zero; matrix[A,A] unit; mu_zero = rep_vector(0,A); unit = diag_matrix(rep_vector(1,A)); } parameters{ cholesky_factor_cov[P,A] alpha; ordered[C-1] beta[P]; vector[A] theta[N]; } transformed parameters{ vector[P] mu[N]; for(n in 1:N){ mu[n] = alpha*theta[n]; } } model{ for(n in 1:N){ for(p in 1:P){ if(y[n,p]!=999){ y[n,p] ~ ordered_logistic(1.7*mu[n][p],1.7*beta[p]); } } } theta ~ multi_normal(mu_zero,unit); to_vector(alpha) ~ normal(0,10^2); for(p in 1:P) beta[p] ~ normal(0,10^2); } |
注意点は、θは多変量正規分布から生成していますが、平均が0ベクトル、共分散行列が単位行列にしてあるので、結局は全部が独立した正規分布から生成しているのと同じです。あと順序ロジスティック分布は、リンク関数を確率モデルに含んでいるので、ロジスティックリンクは省略できます。
Rコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
#functions datastan.make <- function(data,A,C){ P <- ncol(data) return(list(N=nrow(data),P=P,A=A,C=C,y=data)) } initstan.make <- function(data,A){ P <- ncol(data) alpha <- matrix(chol(cor(data))[1:A,],ncol=A,nrow=P,byrow=T) alpha <- alpha / (1.1-alpha^2)^0.5 theta <- as.matrix(scale(dat))%*%solve(cor(dat))%*%alpha init<- list(alpha=alpha,theta=theta) return(init) } N = 500 P = 25 A = 5 C = 5 #stan input modelstan <- stan_model("categorical_fa2.stan") datastan <- datastan.make(dat,A=A,C=C) initstan <- initstan.make(dat,A=A) #variational bayes fit <- vb(modelstan,data=datastan,init=initstan, iter=10000,tol_rel_obj=0.001,output_samples=1000) #stan output print(fit,pars=c("alpha")) print(fit,pars=c("beta")) print(fit,pars=c("theta")) |
Stanコードはcategorical_fa2.stanというものを読み込んでいます。
また、多次元IRTはおそろしく時間がかかるので(潜在変数も同時に推定しているため)、MCMCではなくて変分ベイズで推定しています。変分ベイズは95%信頼区間などはかなり怪しいですが、点推定値については、回帰モデルでない限りはいい感じに推定してくれる(という僕の主観)と思うので、こういう因子分析モデルでは使えそうです。
ただ、vbのデフォルト設定はかなり甘いので、ちょっと設定をいじってます。
識別力の回転
多次元IRTの場合、上に書いたように因子負荷量に制約が必要です。これだと単純構造解にならず、いまいち解釈がしづらいです。そこで、ここでは簡易的に事後分布の平均をとってきて、それをGPArotationの回転関数に入れて回転させる方法を書いてみます。
次のRコードで簡単にできます。
|
1 2 3 4 5 6 7 8 9 10 |
#rotation alpha <- apply(rstan::extract(fit)$alpha,c(2,3),mean) beta <- apply(rstan::extract(fit)$beta,c(2,3),mean) result.promax <- Promax(alpha) load.promax <- result.promax$loadings load.rotmat <- result.promax$rotmat theta <- apply(rstan::extract(fit)$theta,c(2,3),mean) theta.promax <- as.matrix(theta)%*%load.rotmat |
識別力を回転させて、その回転行列をθにかけてやれば、θも回転できます。
ちゃんと推定できてるかチェック
今回はテストように多次元IRTのモデルから乱数を生成して、真値に一致するかをチェックしてみましょう。ただ、Rには順序カテゴリカルの乱数を出してくれるものがないので、Stanを使って乱数を出してみます。
乱数生成用のStanコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
data{ int N; int P; int A; int C; matrix[P,A] alpha; ordered[C-1] beta[P]; vector[A] theta[N]; } parameters{ real temp; } model{ temp ~ normal(0,1); } generated quantities{ int y[N,P]; vector[P] mu[N]; for(n in 1:N){ mu[n] = alpha*theta[n]; } for(n in 1:N){ for(p in 1:P) y[n,p] = ordered_logistic_rng(1.7*mu[n][p],1.7*beta[p]); } } |
ここにαとβ、θをいれてやれば、それに合ったデータyが生成されます。
Rコードは以下です。関数の形にしてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#functions MIRT_data <- function(N=N,pitem=pitem,A=A,C=C,disc=disc,diff=diff){ P <- A*pitem alpha_true <- matrix(nrow=P,ncol=A) for(i in 1:A){ for(j in 1:P){ if(j>=(i-1)*pitem+1 && j alpha_true[j,i] <- disc }else{ alpha_true[j,i] <- 0 } } } beta_true <- matrix(nrow=P,ncol=C-1) for(i in 1:P) beta_true[i,] <- diff theta_true <- matrix(nrow=N,ncol=A) for(i in 1:A) theta_true[,i] <- rnorm(N,0,1) model.random <- stan_model("random.stan") data.random=list(N=N,P=P,A=A,C=C,alpha=alpha_true,beta=beta_true,theta=theta_true) rdata <- sampling(model.random,data=data.random,iter=1,chains=1) dat <- as.data.frame(apply(rstan::extract(rdata)$y,c(2,3),median)) return(list(dat=dat,theta_true)) } N <- 500 #サンプルサイズ pitem <- 5 #因子ごとの項目数 A <- 5 #因子数 C <- 5 #尺度の段階数 disc <- 1 #因子負荷量初期値 diff <- c(-2.5,-0.8,0.8,2.5) #閾値初期値 output <- MIRT_data(N=N,pitem=pitem,A=A,C=C,disc=disc,diff=diff) dat <- output[[1]] theta_true <- output[[2]] |
これでサンプルサイズ500、25項目のデータが生成できます。
上のStanとRのコードで分析した結果は以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
Loadings: [,1] [,2] [,3] [,4] [,5] [1,] 0.994 [2,] 0.992 [3,] 1.156 [4,] 0.992 [5,] 0.862 0.123 [6,] 0.999 [7,] 0.914 [8,] 0.995 [9,] 1.029 [10,] 0.930 [11,] 0.804 [12,] 0.968 [13,] 0.976 [14,] 0.870 [15,] 0.845 [16,] -0.916 [17,] -1.094 [18,] -1.105 0.114 [19,] -1.075 [20,] -0.122 -0.943 [21,] 1.002 [22,] 0.991 [23,] -0.103 1.039 [24,] 1.014 [25,] 0.111 0.962 |
識別力は該当する因子に対して、それぞれ1を真値としました。それなりにうまく推定できているようです。
続いて、閾値。-2.5、-0.8、0.8、2.5が真値です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
[,1] [,2] [,3] [,4] [1,] -2.462413 -0.7813462 0.8352385 2.611353 [2,] -2.555941 -0.8443570 0.7266898 2.632560 [3,] -2.765047 -0.9995234 0.7064590 2.660178 [4,] -2.481259 -0.6747712 0.9921340 2.670267 [5,] -2.366845 -0.5806184 1.0120324 2.559023 [6,] -2.307452 -0.6687736 0.8685212 2.573282 [7,] -2.580331 -0.7563842 0.8520463 2.431250 [8,] -2.836944 -0.8879149 0.6889883 2.256086 [9,] -2.441171 -0.7603130 0.7837924 2.374017 [10,] -2.601652 -0.7024557 0.8383516 2.563616 [11,] -2.287317 -0.6597827 0.9131377 2.775252 [12,] -2.571064 -0.7489278 0.9933323 2.699750 [13,] -2.474953 -0.8050790 0.9023221 2.896048 [14,] -2.444763 -0.8207042 0.8119496 2.545172 [15,] -2.524140 -0.8539099 0.7870610 2.367731 [16,] -2.372706 -0.7526523 0.7824092 2.512122 [17,] -2.375939 -0.8497881 0.8932564 2.826441 [18,] -2.784587 -0.8807199 0.9477899 2.781807 [19,] -2.657058 -0.7600233 1.0026285 2.775923 [20,] -2.493066 -0.8966062 0.8216387 3.183945 [21,] -2.701446 -0.7524835 0.9178492 2.621524 [22,] -2.473794 -0.7924838 0.7964736 2.350835 [23,] -2.548841 -0.8797561 0.7109754 2.681058 [24,] -2.833365 -0.8831064 0.7549298 2.617665 [25,] -2.724647 -1.0215748 0.5857471 2.291645 |
これもうまく推定できているようです。
最後に、θです。これは元のθとの相関を出してみました。対応する因子はズレてますが、0.9近い相関が得られています。Nを増やせばもっと相関は上がると思います。
|
1 2 3 4 5 6 7 |
> cor(theta.promax,theta_true) [,1] [,2] [,3] [,4] [,5] [1,] 0.886459956 -0.043151578 0.007046363 -0.02807225 -0.039666657 [2,] 0.001027467 0.007612685 0.015222919 -0.88405835 0.004439962 [3,] -0.007819860 0.026245460 0.045627580 -0.01748545 0.880945554 [4,] -0.025791803 0.896007369 0.042088778 -0.05470535 -0.046387345 [5,] -0.006982312 0.077074301 0.876676743 0.02679502 0.017743421 |
雑な記事になってすみませんが、以上です。