この記事は、Stan advent calendar 2018の5日目の記事です。
もともと今日は書く予定ではなかったんですが、カレンダーが空いてたので埋めてみよう、という記事です。そんなに準備はできてないです。
竹林さんの3日目の記事、tidybayesは便利そうですね。tidyなみなさんはぜひこちらを使ってほしいんですが、どうも僕は研究ではそもそもデータがきれいなものを扱うことが多いので、そんなにtydyverseにお世話になっていないです。ということもあり、dplyrやggplot2などの文法に慣れていないので、Stanを使うとこもapplyとplotを使うことが多いです。
というわけで、今回は、僕的にStanの結果を非tidyverseで見るための工夫をメモ代わりに書いておこうと思います。すでに知ってることもあると思いますし、tidybayesパッケージとかのほうが便利なこともあるかと思いますが、つらつら書いておきます。
基本的に「俺流」なので、あまり参考にならないかもですが、こういう記事もいいかなと思って。
◆今回の例で使うモデル
この記事の読者はむしろ心理統計にあまり関心がない人が多いかもしれませんが、今回の例では項目反応理論を挙げておきます。その中でも、一般化部分採点モデル(Generalized Partial Credit Model: GPCM)と呼ばれる、順序尺度データに対応した項目反応理論を紹介します。
GPCMはある人iが項目jのカテゴリc(0,1,...K)に反応する確率を次のような関数で表せるとします。
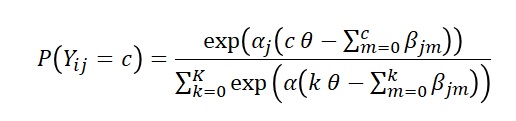
ここで、alphaは識別力パラメータといって、項目がテスト全体の傾向を反映してるかどうかの指標です。betaは閾値パラメータといって、各反応カテゴリの閾値を表しています。
このGPCMをStanでモデルどおりに書くと次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
data{ int N; int P; int S; int Y[N,P]; } transformed data{ vector[S] c = cumulative_sum(rep_vector(1,S))-1; } parameters{ vector vector[S-1] beta[P]; vector[N] theta; } transformed parameters{ vector[S] thr[P]; for(p in 1:P){ thr[p] = cumulative_sum(append_row(0,beta[p])); } } model{ //model for (n in 1:N){ for(p in 1:P){ Y[n,p] ~ categorical_logit(alpha[p]*(c*theta[n]-thr[p])); } } //prior theta ~ normal(0,1); alpha ~ student_t(4,0,5); for(s in 1:S) beta[s] ~ normal(0,10); } generated quantities{ vector[N] log_lik = rep_vector(0,N); for (n in 1:N){ for(p in 1:P){ log_lik[n] += categorical_logit_lpmf(Y[n,p] | alpha[p]*(c*theta[n]-thr[p])); } } } |
走らせるRコードは以下です。GPCMに従って乱数を生成して、それをStanで推定している感じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#setting N <- 200 P <- 10 S <- 5 softmax <- function(x){ exp(x)/sum(exp(x)) } #parameter theta <- rnorm(200,0,1) dat <- data.frame(V1=rep(0,N)) alpha <- 1.2 beta <- c(-2,-0.5,0.5,2) c <- cumsum(rep(1,S))-1 #data generation tempdat <- c() for(p in 1:P){ for(n in 1:N){ temp <- rmultinom(1,1,softmax(alpha*(c*theta[n]-cumsum(c(0,beta))))) for(s in 1:S){ if(temp[s,1]==1) tempdat[n] <- s } } dat[p] <- tempdat } #stan model.irt <- stan_model("GPCM.stan") datastan <- list(N=N,P=P,S=S,Y=dat) fit.irt <- sampling(model.irt5,data=datastan,iter=2000,warmup=1000,chains=4,cores=4) |
◆僕が使っているパッケージ
僕がStanを使うときに使うパッケージは以下です。僕は実はあまりパッケージを使いたくないタイプでして(仕様が変わって使い勝手が変わったり、再現できないのが嫌なタイプ)、極力素のRでコードを書く人間です。なので最小限にしています。
|
1 2 3 4 |
library(rstan) library(psych) library(magrittr) library(bridgesampling) |
rstanを使えばggplot2は勝手に使えるので書いてません。dplyrは使わないのですが、stanfitオブジェクトがアホみたいに容量がでかいので、あまり複製をしたくないため、パイプ演算子は必須です。なのでmagrittrだけ使うことが多いです。
psychパッケージはlogistic関数とか、基本的なのがはいってるので常に入れてます。bridgesamplingはベイズファクターの計算で使います。
◆前もって作っておくと便利な関数
MCMCの結果を見るときに、Rにははじめから入ってなかったり、あるけど重くて使いにくいのがいくつかあるので、ここで紹介しておきます。
まずはMAP推定値をかえすmap()という関数を作ります。これはStanユーザーでは有名な処理です。
|
1 2 3 |
map <- function(z){ density(z)$x[which.max(density(z)$y)] } |
カーネル密度推定を利用して、密度の最大値を推定するものです。
続いて、WAICを返す関数です。looパッケージにwaic関数があるんですが、これ、よくRstudioが爆発するんです(やっと推定終わったーさぁWAICでも見るかーボカーンという地獄)。というわけで自分で定義したものを僕は使ってます。
|
1 2 3 4 5 6 |
waic2 <- function(log_lik){ lppd <- sum(log(colMeans(exp(log_lik)))) p_waic <- sum(apply(log_lik,2,var)) waic <- -2*lppd+2*p_waic return(list(waic=waic,lppd=lppd,p_waic=p_waic)) } |
◆mcmcの結果を見る
ではさっそくMCMCの結果を見てみましょう。僕はパイプ演算子が好き、かつ、一つの処理を1行で書きたいという謎の癖を持っています。
alphaとbetaの推定結果を見る
|
1 2 |
#summary fit.irt %>% print(pars=c("alpha","beta")) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
Inference for Stan model: GPCM5. 4 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=4000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat alpha[1] 1.10 0.00 0.18 0.79 0.98 1.09 1.21 1.46 2607 1 alpha[2] 1.42 0.00 0.22 1.03 1.26 1.40 1.56 1.89 2341 1 alpha[3] 1.21 0.00 0.19 0.87 1.08 1.20 1.33 1.61 2635 1 alpha[4] 1.12 0.00 0.18 0.80 0.99 1.11 1.23 1.49 2231 1 alpha[5] 1.18 0.00 0.19 0.84 1.05 1.17 1.30 1.56 2576 1 alpha[6] 1.42 0.00 0.22 1.02 1.26 1.40 1.55 1.89 2606 1 alpha[7] 1.19 0.00 0.19 0.86 1.06 1.18 1.31 1.59 2368 1 alpha[8] 1.06 0.00 0.17 0.76 0.94 1.05 1.17 1.40 2613 1 alpha[9] 1.40 0.00 0.22 1.01 1.25 1.39 1.54 1.85 2469 1 alpha[10] 1.23 0.00 0.19 0.87 1.10 1.22 1.36 1.64 2958 1 beta[1,1] -1.71 0.01 0.30 -2.34 -1.90 -1.70 -1.51 -1.15 2679 1 beta[1,2] -0.66 0.00 0.22 -1.11 -0.80 -0.65 -0.52 -0.25 2917 1 beta[1,3] 0.43 0.00 0.20 0.03 0.31 0.43 0.56 0.83 2243 1 beta[1,4] 2.24 0.01 0.35 1.61 1.99 2.21 2.45 2.98 2071 1 beta[2,1] -2.14 0.01 0.29 -2.76 -2.33 -2.12 -1.94 -1.65 2028 1 beta[2,2] -0.50 0.00 0.17 -0.82 -0.61 -0.49 -0.39 -0.17 2403 1 beta[2,3] 0.54 0.00 0.17 0.21 0.43 0.54 0.65 0.86 1933 1 beta[2,4] 3.53 0.01 0.58 2.60 3.13 3.46 3.87 4.83 2589 1 beta[3,1] -2.29 0.01 0.33 -3.01 -2.50 -2.27 -2.06 -1.71 2469 1 beta[3,2] -0.38 0.00 0.19 -0.75 -0.50 -0.38 -0.25 0.00 2223 1 beta[3,3] 0.59 0.00 0.19 0.23 0.46 0.59 0.72 0.99 2226 1 beta[3,4] 2.07 0.01 0.32 1.52 1.86 2.05 2.27 2.76 2049 1 beta[4,1] -1.90 0.01 0.31 -2.55 -2.08 -1.88 -1.69 -1.33 2477 1 beta[4,2] -0.57 0.00 0.21 -0.99 -0.71 -0.57 -0.44 -0.18 2446 1 beta[4,3] 0.56 0.00 0.20 0.16 0.43 0.56 0.68 0.96 2030 1 beta[4,4] 2.55 0.01 0.39 1.87 2.29 2.53 2.79 3.40 1917 1 beta[5,1] -2.12 0.01 0.33 -2.82 -2.32 -2.09 -1.89 -1.55 2346 1 beta[5,2] -0.42 0.00 0.20 -0.80 -0.54 -0.42 -0.29 -0.04 2745 1 beta[5,3] 0.28 0.00 0.20 -0.12 0.15 0.28 0.41 0.65 2765 1 beta[5,4] 2.06 0.01 0.31 1.51 1.85 2.05 2.25 2.73 2780 1 beta[6,1] -2.34 0.01 0.31 -3.02 -2.53 -2.31 -2.13 -1.80 2013 1 beta[6,2] -0.37 0.00 0.17 -0.70 -0.48 -0.37 -0.26 -0.03 2155 1 beta[6,3] 0.62 0.00 0.17 0.29 0.50 0.62 0.74 0.97 2062 1 beta[6,4] 1.71 0.01 0.25 1.25 1.54 1.69 1.87 2.23 2285 1 beta[7,1] -1.96 0.01 0.29 -2.58 -2.14 -1.94 -1.76 -1.44 2154 1 beta[7,2] -0.28 0.00 0.19 -0.66 -0.40 -0.28 -0.15 0.09 2734 1 beta[7,3] 0.48 0.00 0.19 0.10 0.35 0.48 0.60 0.86 2479 1 beta[7,4] 2.38 0.01 0.36 1.76 2.14 2.35 2.59 3.14 2183 1 beta[8,1] -2.41 0.01 0.37 -3.22 -2.63 -2.38 -2.15 -1.77 2817 1 beta[8,2] -0.37 0.00 0.21 -0.77 -0.51 -0.37 -0.23 0.05 2665 1 beta[8,3] 0.46 0.00 0.21 0.05 0.32 0.46 0.60 0.90 2820 1 beta[8,4] 1.72 0.01 0.29 1.19 1.52 1.70 1.90 2.33 2895 1 beta[9,1] -2.04 0.01 0.27 -2.61 -2.22 -2.03 -1.85 -1.55 2044 1 beta[9,2] -0.38 0.00 0.16 -0.71 -0.49 -0.38 -0.27 -0.05 2286 1 beta[9,3] 0.61 0.00 0.17 0.28 0.50 0.61 0.72 0.97 1760 1 beta[9,4] 2.21 0.01 0.31 1.66 1.99 2.19 2.40 2.89 1852 1 beta[10,1] -1.92 0.01 0.28 -2.49 -2.10 -1.91 -1.73 -1.41 2076 1 beta[10,2] -0.36 0.00 0.19 -0.73 -0.48 -0.36 -0.23 0.00 2594 1 beta[10,3] 0.57 0.00 0.19 0.19 0.44 0.57 0.69 0.94 2601 1 beta[10,4] 1.92 0.01 0.29 1.40 1.72 1.91 2.10 2.55 2680 1 Samples were drawn using NUTS(diag_e) at Wed Dec 05 16:37:56 2018. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). |
僕はprintが好きです(謎)。digits=で簡単に桁数も変えられます。
rhatだけを見たい場合は、stan_rhatが便利です。
|
1 |
fit.irt %>% stan_rhat |
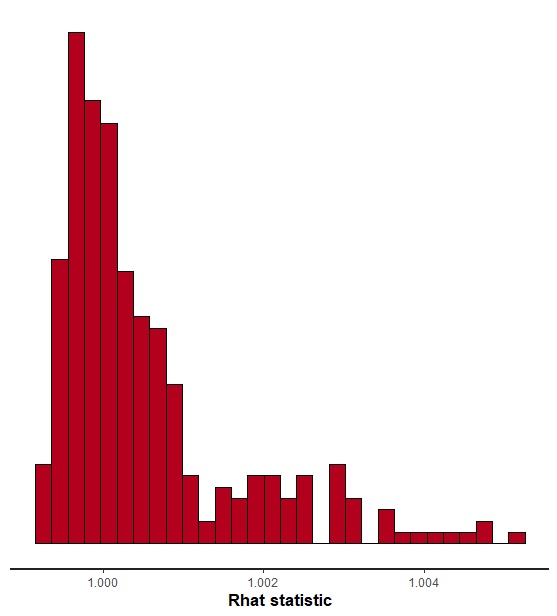
うまくいってそうです。
自己相関の程度を見るのはessが便利。
|
1 |
fit.irt %>% stan_ess |
Stan2.18からESSの計算方法が変わって、1を超えることがあるようですね。
WAICは次のようにやります。さっき作ったwaic2関数を使います。
|
1 2 |
#WAIC fit.irt %>% rstan::extract() %$% log_lik %>% waic2 |
◆パラメータを取り出す
識別力母数alphaは項目ごとにあるので、applyを使います。って、別に何も特別なことではないですけども。ここでは先程作ったmap関数を使って、MAP推定値を取り出してみます。
|
1 |
fit.irt %>% rstan::extract() %$% alpha %>% apply(2,map) %>% data.frame(alpha=.) |
縦に表示したいがために、最後にdata.frameを使ってます。別にここはいらないです。
|
1 2 3 4 5 6 7 8 9 10 11 |
alpha 1 1.106847 2 1.425027 3 1.214761 4 1.114890 5 1.190869 6 1.415996 7 1.193040 8 1.054754 9 1.404332 10 1.236946 |
困難度母数のbetaは項目✕カテゴリの2次元配列なので、apply(c(2,3), mean)とかになります。
|
1 |
fit.irt %>% rstan::extract() %$% beta %>% apply(c(2,3),mean) %>% print(digits=3) |
|
1 2 3 4 5 6 7 8 9 10 11 |
[,1] [,2] [,3] [,4] [1,] -1.71 -0.662 0.434 2.24 [2,] -2.14 -0.495 0.539 3.53 [3,] -2.29 -0.378 0.593 2.07 [4,] -1.90 -0.574 0.557 2.55 [5,] -2.12 -0.416 0.278 2.06 [6,] -2.34 -0.369 0.623 1.71 [7,] -1.96 -0.278 0.476 2.38 [8,] -2.41 -0.368 0.462 1.72 [9,] -2.04 -0.381 0.609 2.21 [10,] -1.92 -0.356 0.567 1.92 |
最後にprintで桁数を変えるのもポイント。
識別力母数を項目ごとに事後分布を見る場合は次のようにやってます。
|
1 |
fit.irt %>% rstan::extract() %$% alpha[,1] %>% density %>% plot |
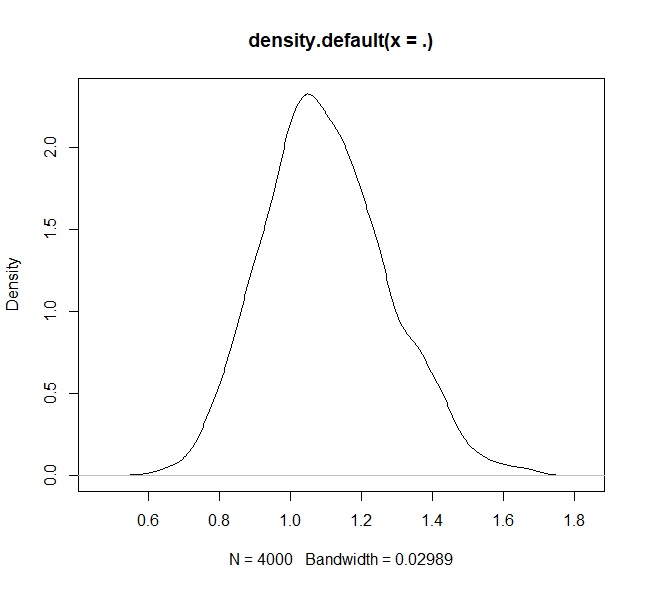
出た!シンプルな図!ploter魂が震えますね。
でも流石にシンプルすぎるので、たまにはこんなのもします。rstan内蔵の関数を使います。
|
1 |
fit.irt %>% stan_dens(pars="alpha[1]",separate_chains = T) |
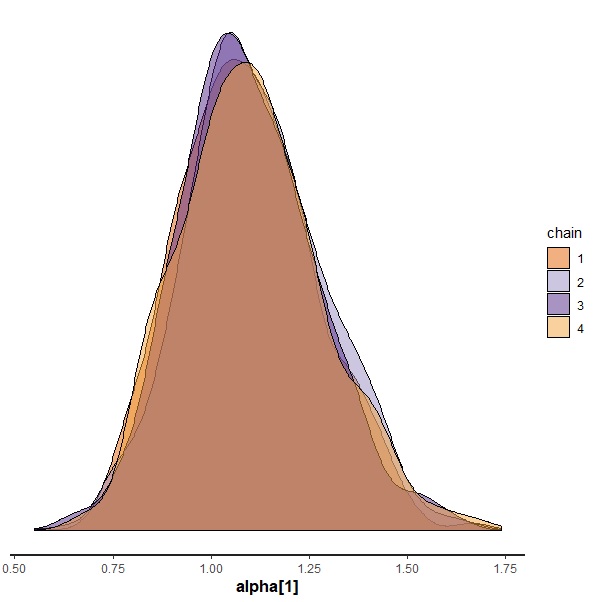
収束してるのもよくわかってよい。
traceplotは普通にrstan内蔵のものをよく使ってます。
|
1 |
fit.irt %>% stan_trace(pars="alpha[1]") |
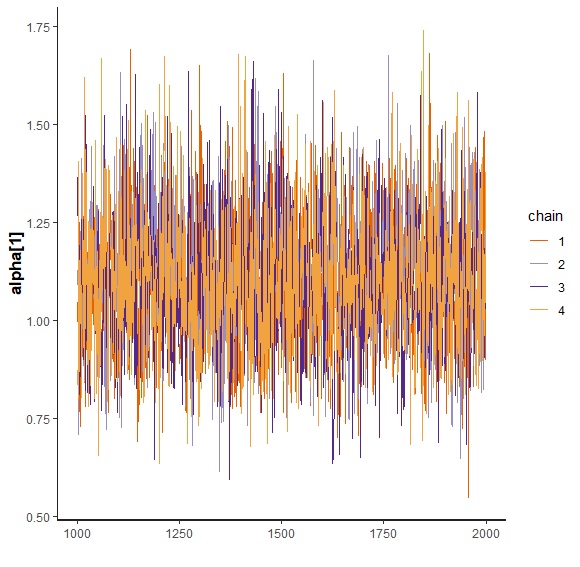
潜在変数を取り出します。
|
1 2 |
theta <- fit.irt %>% rstan::extract() %$% theta %>% apply(2,mean) hist(theta) |
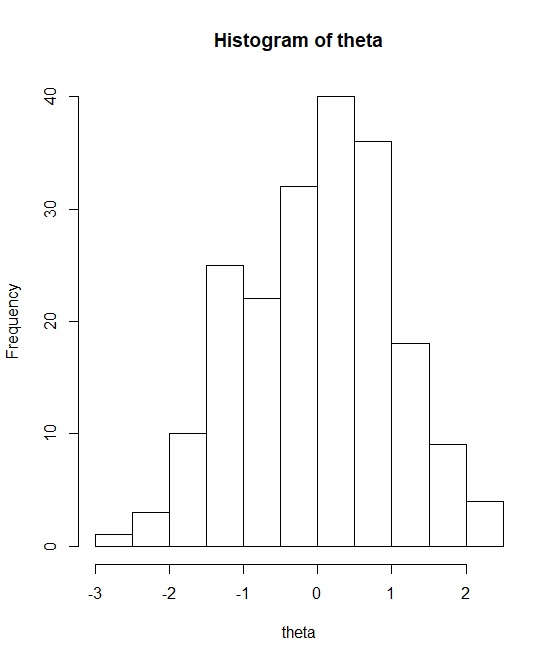
味わい深いですね。