この記事では,カテゴリカル・データの相関係数である,ポリコリック相関係数について書きます。
カテゴリカルデータの相関係数
心理尺度でデータを測定した場合、5件法や7件法によるリッカート法を使うことが多いと思います。
リッカート法とは、ある質問について、当てはまる程度を1.まったく当てはまらない~5.非常に当てはまる、といった感じで5段階(場合によっては3段階や7段階など)で評定を求める方法です。
このようなリッカート法を使ってデータを収集する場合、得られた値を「間隔尺度」として扱って分析することがほとんどです。これはもちろん、間隔尺度のほうが扱える分析法が圧倒的に多いので、便利だからです。
しかし、心理学者の中でも、リッカート尺度は本来「順序尺度」なので、間隔尺度として扱うことに限界を感じている研究者も多いです。その理由としては、
- 値に与えられているラベル(まったく当てはまらない、など)間の間隔がすべて等しい、という仮定が怪しい
- 例えば5件法なら、1より小さい値、あるいは5より大きい値を得られないので、測定上の制限がある
といったものが主な理由です。上のような特徴は、間隔尺度というよりむしろ順序尺度の性質です。
そこで、近年使われ始めているのがカテゴリカルデータの分析法です。これらは、順序尺度水準のデータを、順序尺度の性質を仮定したまま分析する方法です。カテゴリカルデータ分析法を使えば、順序尺度を間隔尺度としてみなさなくても、相関分析や因子分析が可能です。
そういったカテゴリカルデータの相関関係を明らかにする方法として,ポリコリック相関係数があります。ポリコリック相関係数は、一言でいえば、「背景に連続値が仮定される順序尺度の、真の相関係数を推定する」方法です。もう少し詳しく言うと、以下のようになります。
リッカート尺度などは、本来連続的な強度を持つと考えられる心理的な特性を、測定上順序尺度で測定しています。その「背景にある連続的な心理特性」を、順序尺度のデータから推定し、その変数間の相関係数を推定するのがポリコリック相関係数です。
ポリコリック相関係数の、数理的な話については小杉先生の資料がとても参考になります(上から5番目の資料)。日本語ではこれが一番わかりやすいと思います。
数理的な話は置いといて、どう便利なのか、本当にちゃんと真の相関なんて推定できてるのか、という話は続きを参照してください。
ポリコリック相関係数は、本当に真の相関を推定できるの?
ポリコリック相関係数は、順序尺度間の真の相関係数を推定するわけですが、ここで、「真の相関係数」というのがわかりにくいかと思うので、以下のような例を挙げてみます。まず、相関係数が0.7であるような2変数1000人のデータを作成します。
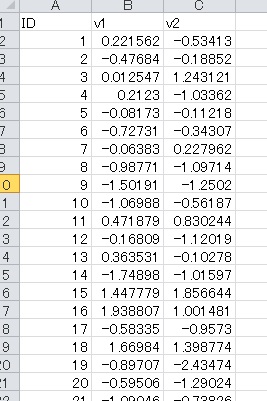
以下のようなデータを正規乱数から作ってみました。
正規乱数から作っているので、この二つのデータは標準正規分布に従っています(つまり標準得点)。記述統計量を見てみましょう。
微妙に違いますが、平均が0、標準偏差が1に近いデータになっています。相関係数は、ぴったり0.7です。
さて、このデータを「真のデータ」とします。つまり、「連続的な強度を持った心理特性」です。しかし、実際はリッカート尺度などで順序尺度として測定されます。なので、実際にこれらの連続値を我々が知ることはありません。
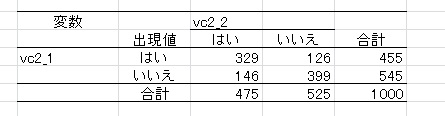
ここで、仮にこの心理特性を「はい・いいえ」の2件法で測定したとしましょう。わかりやすいように、0より小さい値を「はい」、0より大きい値を「いいえ」にしたとします。すると、以下のようなクロス表が得られます。
もともとの相関係数が0.7なので、2件法にしても、対角の度数が多くなっています。ではこのデータの相関係数を、普通に計算してみるとどうなるでしょうか。
連関係数、順位相関、積率相関ともに0.454と計算されました(2値データの場合は、すべて一致します)。真値である0.7とは程遠い値です。
このように、真の心理特性間の関係が0.7と高くても、順序尺度水準で測定されたデータをそのまま分析してしまうと、0.45とかなり小さく推定されてしまいます。これも一種の相関の希釈化といえます。
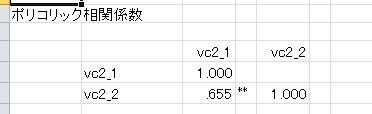
それでは、ポリコリック相関係数を計算してみましょう(2値の場合は、テトラコリック相関ともいう)。
0.655になりました。これは、ピアソンやスピアマンの相関係数0.454に比べて、かなり真値に近づいています。
このように、ポリコリック相関係数は順序化されたデータから、真の相関係数をよりよく推定しているのがわかります。
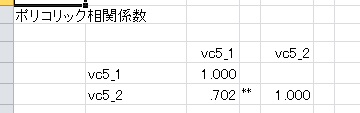
ためしに、5件法でも試してみましょう。-1.3以下を1、-0.5以下を2、0.5以下を3、1.3以下を4、それより大きい場合に5に変換し、同様に各種相関係数とポリコリック相関を算出しました。
5件法の場合、2件法に比べてかなり真値に近くなっていますが、まだ少し小さいです。それに対してポリコリック相関の場合は、ほぼ真値と一致しています。
ポリコリック相関係数のからくり
数理的なところは省きます。そちらに興味ある人は、小杉先生のページを参照してください。まず、ポリコリック相関係数はデータとしてクロス表を使います。
もう一度、2件法の時のクロス表を見てみましょう。
クロス表を見れば二つの変数のはい同士・いいえ同士の度数が多いことから、正の相関があることがなんとなくわかります。でも、このはい・いいえのデータはあくまで真の値ではなく、測定上で順序化されたものです。このとき、以下のように考えます。
「もし背景に連続値が仮定されているとすれば,このクロス表が得られるとき,その連続値の間にどれくらい相関係数があるのがもっともらしいか」
この発想は、最尤推定法と呼ばれるものです。最尤法は手元にあるデータが得られたとき最も尤もらしいモデル(推定値)を推定する方法です。ポリコリック相関係数の場合は、データのクロス表が最も得られやすい相関係数を推定するわけです。
もちろん、何の仮定もなしに推定はできません。ポリコリック相関係数は、背景にある連続値が二変量正規分布に従っていると仮定します。ここで重要なのは、データが正規分布にしたがっている必要はない、ということです。あくまで背景に仮定されている心理特性が正規分布に従っているという仮定です。この仮定は、それほど無理なものではないので、使いやすい方法だといえます。
また、最尤法を使って推定するので、検定も「Wald検定」を用います。これは、推定値を標準誤差で割ると正規分布に従うことを利用した検定法です。検定統計量はz値です。t分布を使わないので自由度は登場しません。
ポリコリック相関係数の限界
便利なポリコリック相関係数ですが、上の仮定によって、次のような制限があります。
- 背景に連続値が仮定されないような順序尺度には使えない
- 真値が正規分布にならないような変数には使えない
1.は例えば、男性・女性といったもともと2値になるデータには使えません。あくまで、本当は連続値だけど測定上順序尺度になる変数だけが対象になります。
2.は例えば「一日にメールを送る回数」といった出来事の頻度は、たいてい正規分布にならないので、それを順序尺度で尋ねたとしても、ポリコリック相関係数が正しい推定をするとは限りません。
このように、ポリコリック相関係数も万能ではないのです。
順位相関係数との違い
順序尺度の相関といえば、ケンドールやスピアマンの順位相関が有名です。
しかし、すでに上で見たように、スピアマンの相関係数よりもポリコリック相関係数は正確に真値を推定できます。よって、心理尺度の場合はポリコリック相関係数のほうに軍配が上がります。
一方、順位相関は背後に連続値を仮定していませんし、分布も仮定していません。なので、背後に連続性が仮定できないデータとの相関を見る場合は、順位相関のほうがいいでしょう。
ポリコリック相関係数は、あくまでパラメトリックな方法である、ということは覚えておく必要があります。
連続変量と順序尺度との相関
ポリコリック相関は、順序尺度間の相関ですが、連続変量と順序尺度間の相関を見る場合はどうすればいいでしょうか。その場合のために、別に「ポリシリアル相関係数(多系列相関)」というのがあります。
これは、連続変量は「データが」正規分布していることを仮定して、順序尺度は背景にある連続値が正規分布していることを仮定します。その仮定の下で、相関係数を推定します。
要はデータの種類が違うだけの話で、それ以外はポリコリック相関係数と同じです。
ついでに、連続変量同士に対してポリコリック相関係数を計算すると、ピアソンの積率相関と同じ値になります。試しに元のデータに対してポリコリック相関を計算すると、0.700となりました。
ソフトウェア
ポリコリック相関係数は、SPSSは計算してくれません。
しかし、ネットを探せばいろんな人がいろんなところでポリコリック相関係数を計算するプログラムを作っています。
まず第一に挙げられるのはRです。Rのpolycorパッケージにある、polychor()関数で計算可能です。ポリシリアルもpolyserial()関数で可能です。
後、このブログにあるHADがポリコリック相関係数(ポリシリアルはまだ実装してません追記:HAD11からポリシリアル相関も計算可能になりました)計算できます。
Mplusでも変数をカテゴリカル変数として指定すれば、計算できます。
ポリコリック相関係数を使った応用的分析
限界はありますが、心理尺度データに対しては強い味方です。この相関係数を使うと以下のような応用的分析が可能です。
- カテゴリカル因子分析(項目反応モデル)
- カテゴリカル回帰分析(プロビット回帰)
- 構造方程式モデリング(マルチレベルモデルを含む)
もっともわかりやすい応用例は、ポリコリック相関行列を使った因子分析でしょう。
順序尺度で測定した心理変数を因子分析するときに、ポリコリック相関分析を使えれば、より正確に因子得点を推定できます。
また、実はカテゴリカル因子分析は項目反応モデルと数理的には同じ方法です(推定法は違います)。
ポリコリック相関係数を使えば項目反応モデル(段階反応モデル)も実行できます。とはいえ、そのままポリコリック相関係数を使うわけにいかない(標準誤差で重みを付ける必要がある)ので、専用のソフトウェアが必要です。
Mplusはカテゴリカルデータ分析に強いソフトウェアです。
他に、カテゴリカル回帰分析や、構造方程式モデリングも可能です。
これらの方法は、従属変数が順序尺度の場合の回帰・パスモデルです。ロジスティック回帰分析とよく似たことが可能です(ロジスティック関数の代わりに、累積正規関数を用いる)。
HADもカテゴリカル因子分析が可能です。ポリコリックあるいはポリシリアル相関の標準誤差を重みに使って,重みつき最小二乗法で推定します。ただ,Mplusのように頑健標準誤差によって重みづけしていないので,得られたカテゴリの背後にある分布が正規分布から逸脱している場合,一致推定量にならない可能性があります。今後,改良していく予定です。
まとめ
このように、順序尺度を適切に扱えば、そのまま間隔尺度とみなして分析するよりも、より正確にモデルを推定できます。調査で尺度をよく使う人は、限界も含めて性質をよく理解しておけば、どんどん利用すべき方法だと思います。