HADver10から,一般化線形モデルを実行できるようになりました。この記事では,一般化線形モデルの説明とともに,HADで一般化線形モデルを実行するための方法について解説します。
※2015年12月11日,追記しました。
なお,一般線形モデルと一般「化」線形モデルは別物です。このあたりの解説も含めて,以下の記事をどうぞ。
なお,HADについてはこちらの記事を参照してください。
一般化線形モデルって何?
回帰分析や分散分析は,目的変数を説明変数の線形結合(足し算)で予測する,という点において共通しています。よって,この二つをまとめて「一般線形モデル(General Linear Model; GLM)」と呼びます。ただ,普通に線形モデルと呼ぶこともあります。
一般線形モデルは,主に最小二乗法を使って,目的変数を予測します。なので検定方法は主にt分布やF分布を用います。一般線形モデルの仲間には,平均値の差の検定(t検定),分散分析,重回帰分析,共分散分析,多変量分散(回帰)分析などがあります。
このとき,目的変数の残差について正規分布を仮定します。よって,目的変数は(正規性を持った)連続変量である必要があります。もし順序尺度だったり,名義尺度だったり,天井効果や床効果が出ているようなデータに対しては,妥当な推定結果を得ることができません。特に,標準誤差の推定がうまくいかず,検定結果を誤ってしまうことがあります。
そこで,目的変数が正規性を持たないデータだったり,順序尺度や名義尺度だったりする場合に利用されるのが,「一般化線形モデル(Generalized Linear Model; GLM,あるいはGZLM)」です。一般化線形モデルは,目的変数に様々な特徴を許す,一般線形モデルです。つまり,一般線形モデルを包含する上位モデルといえます。
一般化線形モデルは,目的変数の特徴を多様に表現するために,残差の分布と,リンク関数という二つのオプションを組み合わせます。
残差の分布は,正規分布はもちろん,二項分布,ポアソン分布などを利用できます。二項分布は0と1のような2値データを扱うことができる分布で,順序尺度や名義尺度に適用できます。ポアソン分布はイベントの生起頻度のように,0以上の離散値を扱うことができる分布で,カウントデータに適用できます。また,正規分布を拡張して,途中でデータが打ち切られているような打ち切り正規分布を残差に仮定することもできます。
リンク関数とは,線形モデルを目的変数の分布にうまくつなぐための関数のことです。例えば,線形モデルでは予測値が―∞~∞の値を取りえますが,二項分布は確率が0~1に収まらなければなりません。よって,無限の範囲を取るデータを0~1に収めるために,ロジット関数を適用するなどの処理を行います。同様に,ポアソン分布は非負である必要があるので,対数関数を用いてデータが負の値にならないように変換します。
一般化線形モデルでは,よく使われる残差の分布とリンク関数はセットが決まっています。二項分布にはロジット関数やプロビット(累積正規)関数,ポアソン分布には対数関数,対数正規分布やガンマ分布も対数関数が用いられます。ただし,これらを自由に組み合わせることも可能です(場合によっては意味がない組み合わせもありますが)。
また,一般化線形モデルでは,推定法は主に最尤法を用います。よって,検定統計量はZ値になります。検定統計量にZ値を用いると,t値を用いる方法に比べて,小サンプルでは第一種の過誤の確率が高くなります。ただし,大サンプル(100程度以上)の場合は,最小二乗法よりもより精度の高い(標準誤差を小さく)推定ができます。
ただし,近年ではベイズ推定も簡単にできるようになってきました。こちらについてはまた改めて記事を書こうと思います。
HADで扱える一般化線形モデル
HADでは,以下のような一般化線形モデルを実行できます。
・線形回帰分析(連続変量の回帰分析)
分布は正規分布,リンク関数は使いません。いわゆる,重回帰分析と同じです。重回帰分析と異なるのは,推定方法が最尤法である点だけです。
・対数正規分布回帰(連続変量の回帰分析)
分布は対数正規分布,リンク関数は対数リンクです。モデル的には従属変数を対数変換してから回帰分析したものと結果は一致します。ただし,尤度やAICを参照したい場合は,対数変換をするのではなく,対数正規分布で直接モデリングしたほうがいいでしょう。
年収などは対数正規分布に従う典型的な変数です。
・順序回帰分析(順序尺度データの回帰分析)
分布は二項分布,リンク関数はロジットとプロビットを選択できます。データが順序性を持ったカテゴリカルデータに適用できます。カテゴリ数は15以下である必要があります。数値は整数でなくてもよく,小数点や負数も扱うことができます(ただし,順序尺度として扱います)。
・二項回帰分析(割合データの回帰分析)
分布は二項分布,リンク関数はロジットとプロビットを選択できます。データが最大生起数のうち,いくつ生起したか,という割合を表すデータに適用できます。入力は,生起数と最大生起数をそれぞれ行います。例えば,友人ネットワークの中で何人が該当するか,といった割合を目的変数にしたい場合に利用できます。度数が多い場合(100以上)はポアソン回帰のほうが安定します。
・ポアソン回帰分析(カウントデータの回帰分析)
分布はポアソン分布,負の二項分布,一般化ポアソン分布から,リンク関数は対数関数のみ選択できます。データが非負の整数であるような生起頻度を表すデータに適用できます。例えば,1か月で喧嘩した回数や,1週間のうちで何回友人とメールしたか,といったデータに適用できます。1か月や1週間など,人によって期間が異なっている場合は,その情報をオフセット項に入力することで,期間を調整した分析もできます。
また,負の二項分布や一般化ポアソン分布はポアソン分布をより拡張した分布です。ポアソン分布は平均と分散が等しい分布ですが,分散が平均より大きいデータの場合,過分散となり,標準誤差の推定が正しくなくなります。一方,負の二項分布は過分散を許す分布で,一般化ポアソンは過分散と過小分散を許します。さらに,一般化ポアソン分布はデータが整数でなくてもよく,非負の実数に適用できます。
・トービット回帰分析(打ち切りデータの回帰分析)
例えば,高校生の塾や予備校への投資額は,高校の偏差値と相関がありますが,偏差値が一定より小さくなると投資額が0の人が多くなります。このようなデータ,つまり子どもの教育への投資は,0で打ち切られてしまっている,と言えます。あるいは,心理尺度でも反応段階が5段階だと,多くの人が5を付けてしまって,得点が5で打ち切られてしまうような「天井効果」という現象もまれに生じます。
このようなデータに対して,打ち切られた正規分布を仮定する回帰係数が用いられます。トービット回帰分析とは,打ち切り点よりも小さい(大きい)データが仮に打ち切られずに測定されていた場合に全体として正規分布になるように補正する回帰分析です。
HADでは,下側打ち切り,上側打ち切り,両側打ち切りの3つが選択できます。
・名義回帰分析(名義尺度データの回帰分析)
分布は二項分布,リンク関数はロジットのみが選択できます。いわゆる,多項ロジスティック回帰分析です。データに順序性がなくてもよく,それぞれのカテゴリに対する反応確率を予測します。HADでは,データは小数でも負数でも分析できます。
HADでの一般化線形モデルの実行方法
まず,HADを起動し,「回帰分析」のオプションボタンを押します。すると回帰分析用のモデリングスペースが開くので,「一般化線形モデル」を下から選択します。
つぎに,目的変数のところにあるオプションボタンから,目的変数の性質を選択します。「連続」の場合は線形回帰,「順序」を選ぶと順序回帰,「カウント」を選ぶとポアソン回帰,「打ち切り」を選ぶとトービット回帰,「名義」を選ぶと多項ロジスティック回帰が実行されます。
モデリング方法は回帰分析と同じですので,回帰分析の記事を参照してください。
目的変数が割合データの場合,データとともに,総生起数を入力する必要があります。全データで総生起数が等しい場合は,以下の図ように総生起数を直接数値で入力します(ここでは,5と入力しています)。もし,サブジェクトごとに異なっているなら,総生起数がデータとして入力されている変数名を指定します。
カウントデータの分析(ポアソン回帰分析)では,オフセット項を指定できます。オフセット項とは,回帰係数が1に固定される説明変数のことで,リンク関数に対数関数を用いるポアソン回帰の場合などに役立ちます例えば,生起頻度を測定した期間がサブジェクトによって異なる場合,測定した期間を重みづける必要が生じます。しかし。ポアソン分布は非負の整数しかとらないため,割り算した値を目的変数にすることができません。そういうときに,オフセット項として測定期間を指定しておけば,データを生起頻度にしながらも,期間を重みづけたポアソン回帰による推定値を得ることができます。
オフセット項を利用する場合は,重みづけたい変数名をオフセットのところに指定してください。
ロバスト標準誤差について
ロバスト標準誤差については,別の記事でも書きましたが,ここでも書いておきます。
ロバスト標準誤差は,一般化線形モデルが仮定する残差の分布の特徴とデータが適合していない場合でも,より妥当に調整した標準誤差のことです。つまり分布の仮定にたいしてロバスト(頑健)なわけです。
たとえば,ポアソン回帰分析を考えてみると,ポアソン分布は平均と分散が等しいことを仮定しています。しかし,データによっては平均よりも分散のほうが大きくなる,過分散が生じることがあります。ポアソン回帰分析はこの過分散にたいして脆弱で,標準誤差を正確に推定できなくなります。
そこで,ロバスト標準誤差を推定すると,過分散に対しても頑健な検定を行うことができるようになります。このように,一般化線形モデルではロバスト標準誤差はとても重要な意味を持ちます。
ただし,なんでもロバスト標準誤差で推定すればいいというものではありません。まずはデータに合った分布やモデルを選択することを試みるべきでしょう。たとえば,ポアソン分布の過分散は負の二項分布で推定してからロバスト標準誤差で補正する,という方が望ましいでしょう。
一般化線形混合モデルとクラスタ標準誤差について
同じ参加者が複数回反応するような反復測定データや,複数の学校をサンプリングした後,個人をさらにサンプリングするといった二段抽出データは,残差に局所的な相関(個人内・グループ内の類似性)が生じます。一般化線形モデルでも,残差の独立性は適切な検定を行う上で必要な仮定で,この仮定の逸脱に対して,かなり脆弱です。よって,データの非独立性を調整するような手法が必要です。
一般化線形混合モデル(Generalized Linear Mixed Model)は,一般化線形モデルに変量効果を同時に推定することができる手法です。変量効果とは,回帰係数のように固定値を推定するのではなく,個人がグループの変動を分散によって表現したものです。さきほど挙げたように反復測定データの場合は個人内に局所的な相関が生じますが,この相関を変量効果で推定してやれば,残差の独立性は担保されます。それによって,適切な検定を行うことができるのです。
しかし,一般化線形混合モデルは推定が難しいのです。残差の局所的な相関が,一つの変量効果だけで推定できれば,それほど難しくはないですが,複数の変量効果が重なると積分計算が増えて,数値計算にとても時間がかかったりします。HADには一般化線形混合モデルが入っていませんが,それは作者の数学的な素養が原因だったりします。要は,ようわからん。ただし,一般線形混合モデルの亜種であるHLMはHADでも利用できます。
そこで,HADでは変量効果を推定せずとも「残差の非独立性に対しても頑健」な標準誤差である,クラスタ標準誤差(clustered robust standard error)を推定することで対処しました。クラスタ標準誤差を用いれば,残差の局所的な相関を調整した標準誤差を推定するので,少なくとも検定では間違いを犯しません。
以下のように,HADのHLMと一般化線形モデル(連続データに対する)の結果を比較してみましょう。
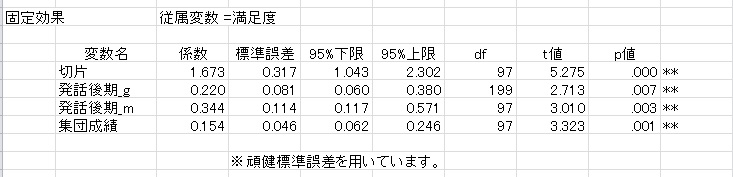
HLMによる結果
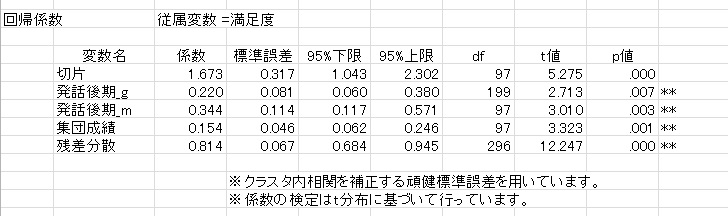
一般化線形モデルのクラスタ標準誤差の結果
上のように,集団内の人数がすべて等しい場合は,HLMと一般化線形モデルwithクラスタ標準誤差の結果は一致する(ただし,適切な中心化をした場合)のです。推定結果が違う場合でも,それほど大きな差はないはずです。
よって,HADでグループ内の類似性があり,順序データやポアソン分布を使った分析をしたい場合は,クラスタ標準誤差にチェックを入れて推定してみてください。
ただし,一般化線形混合モデルが不要である,ということではありません。あくまで代替手段である,ということを認識して利用してください。特に,サンプルサイズが小さい場合はロバスト標準誤差やクラスタ標準誤差ではバイアスが大きくなることが知られています。そういう場合は,検定にt分布を用いるなどの工夫が必要でしょう。また,個人内・グループ内の局所的な相関や回帰係数のグループ間変動などをちゃんと推定して評価したい場合は,一般化線形混合モデルが必要となります。
以上がHADによる一般化線形モデルの説明です。