HAD17.10をアップしました。
HADについてはこちらを御覧ください。
今回増えた機能は、傾向スコアを用いた因果効果の推定と、重みつき重回帰分析です。どちらも関連し合う機能です。
傾向スコアを用いた因果効果の推定は、さまざまな方法がありますが、HADでは逆確率重み付け推定をt検定の機能に追加しました。
傾向スコアや逆確率重み付け推定については別の記事でのちほど解説します。ここでは、HAD17.10でどうやって傾向スコアをつかった推定ができるかを解説します。
◆傾向スコアの推定
傾向スコアの推定方法もいろいろありますが、HADではロジスティック回帰分析を使って簡単に計算ができます。
いま、2つのグループ(条件)の作業での満足度に違いがあるか知りたいとします。しかし、そのグループは無作為割り当てではなく、その作業中の発話量や集団成績やメンバーの会話スキルが交絡している可能性があるとします(架空の研究の話です)。
心理学ではこういう場合、従来では共分散分析を行って、交絡変数を統制した効果を推定します。しかし、交絡変数の影響の仕方が線形でなかったり、群間で等しくなかったりすると、正しい因果効果の推定はできません。ここで傾向スコアを使って、逆確率重み付け推定をすると、うまくいくことがあります。もちろん傾向スコアによる分析にも条件(どちらの群に割り当てられるかは、共変量で完全に説明できるという強く無視できる割り当て条件)がありますが、共分散分析よりは仮定が弱いです。詳しくは別記事で紹介します。
傾向スコアは、群分けしている変数(今回なら条件という変数)に対して共変量でロジスティック回帰を行ったときの予測確率として計算できます。HADでそれを計算するには、ロジスティック回帰分析をするときに「残差得点を出力」をチェックしてください。
下の図の右下あたりにチェックが入ってると思います。

すると以下のような出力がでます。
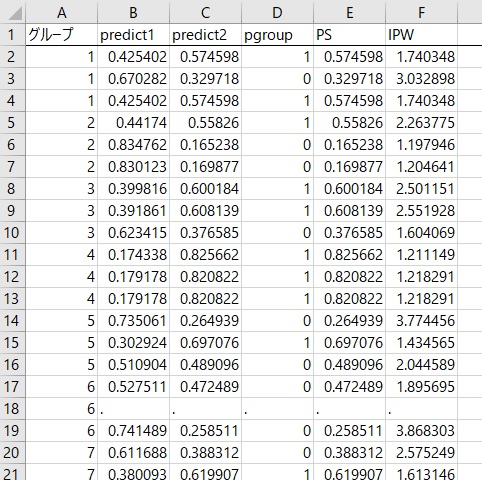
PSとあるのが傾向スコアです。そして、IPWは各群に所属する確率の逆数で、後に述べる逆確率重みづけで使います。これから書く話では、基本的にはIPWのほうを使います。
傾向スコアの使い所は、この値が近い人でマッチングしたり、層分けをしたりして、共変量の影響をなくした上での因果効果の推定を行うときです。しかし、これらの方法は、因果効果の標準誤差の推定ができなかったり、サンプルサイズが減ったりと、あまり効率的ではありません。
そこで傾向スコアをつかった逆確率重み付け推定というのが有力だと言われています。
◆重み付け回帰分析
重みをつけるとは、データの影響力をそれぞれ変えるということです。たとえば、重みが1,2,3,4とあれば、最初のデータはそのまま、2番めのデータは2つ分のデータが、3番めは3つ分あるように計算します。重みつき平均値は、データに重みをかけて足し、最後にサンプルサイズではなく重みの総和で割ります。
しかし、標準誤差の推定は手計算では難しいので、HADでは重み付き回帰分析の機能を実装しました。
やり方は簡単で、重回帰分析のところに「重み→」というのが増えているので、そこにさきほど出力したIPWを指定します。

すると、以下のような結果が得られます。
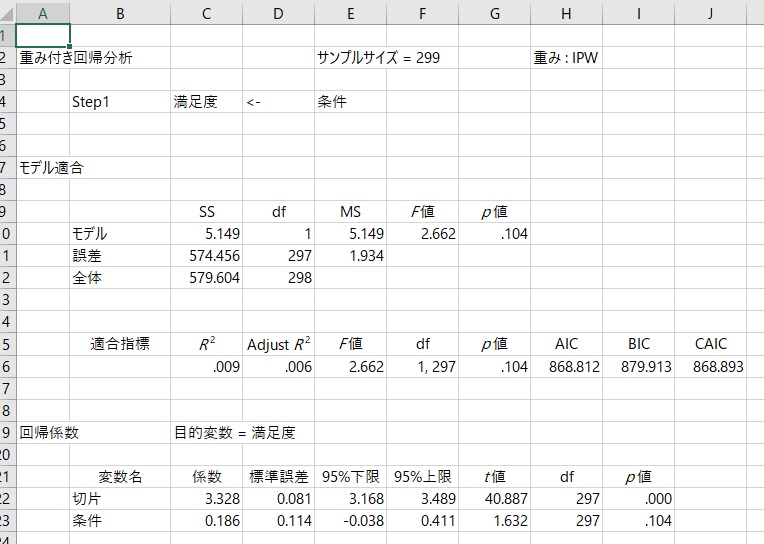
これで得られた回帰係数が、逆確率重み付け推定量です。
◆傾向スコア分析
もちろんこれでもいいのですが、傾向スコアの逆確率の出力など、いろいろ手間がかかります。そこで、分散分析のオプションに、傾向スコア分析というのを追加しました。これで共変量に指定した変数を使って、HAD内部で傾向スコアを計算し、自動的に逆確率重み付け推定ができるようになります。
下の図のように、分散分析で右下にある「傾向スコア分析」をチェックしてください。そして、モデル→に共変量と群分け変数の両方を指定し、共変量→のところに共変量だけを指定します。
注意が必要なのは、群分け変数は必ず2群でないとダメで、また多要因の分析はできません。
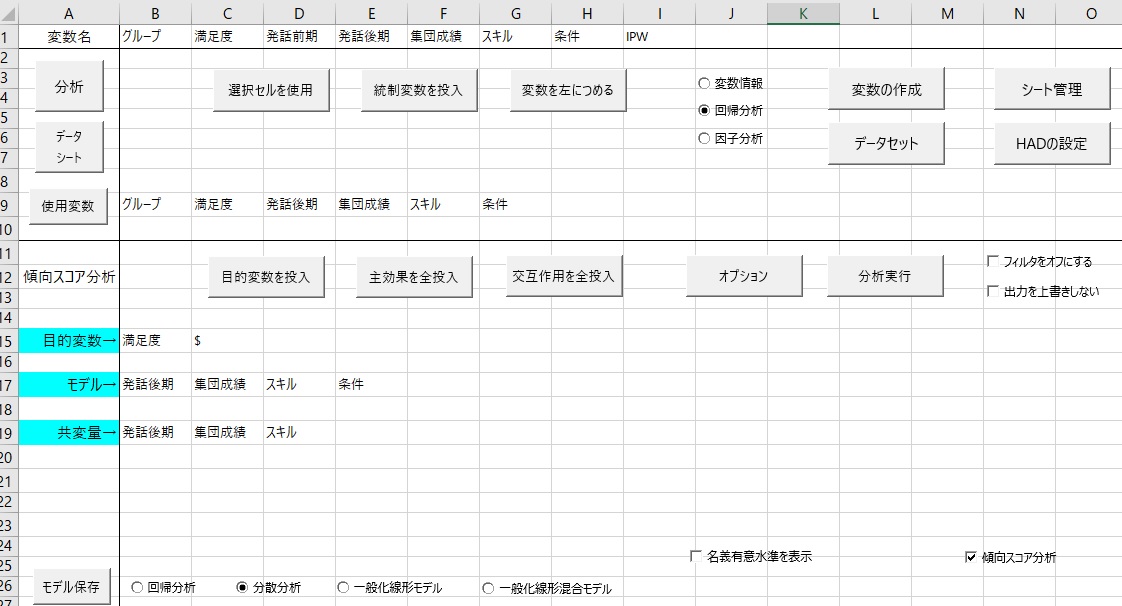
指定はこれだけで、あとは分析実行を押せば、下の図のような結果が得られます。
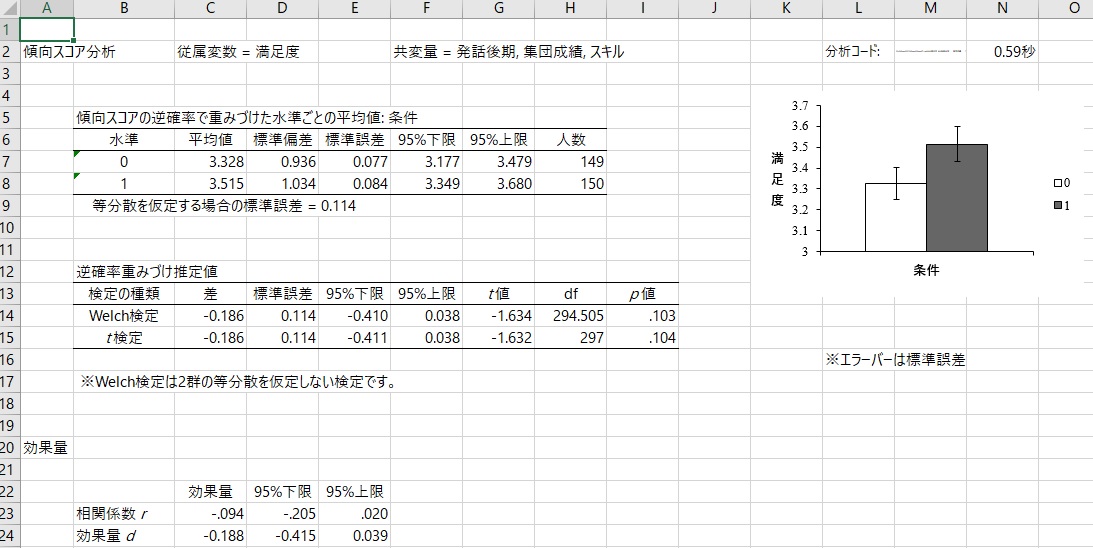
上の重み付き回帰分析と結果が一致しているのがわかると思います。
傾向スコア分析では、等分散を仮定しない(Welch検定)因果効果の推定も出力し、また効果量の信頼区間も推定します。ただ、効果量dの信頼区間は、Welchではなくて下のt検定の結果に対応するので、注意が必要です。
HADのサポートページを作りました。いわゆる「投げ銭」ですが、研究資金などにしようと思います。よかったらぜひ。