リッカート式尺度は何を測っていて、なぜ尺度平均値を使うのか

 

 

心理学以外の研究者や、学部生によく聞かれる質問に、「心理学ではリッカート尺度を使った研究が多いが、あれは大丈夫なのか」というのがある。大丈夫って何よ。

いや、言いたいことはわかる。自己評定式の質問紙調査でリッカート尺度を使った測定って、何を測っているのか、ちゃんと測れてるのか、得点化はそれで大丈夫なのか、などなど疑問はたくさん出てくる。

人間の適応力はすごいもので、2年生で上の疑問を持っていても、4年生にもなると「尺度、大丈夫」ってなっちゃう。でも逆に、尺度をあまり使わない分野の博士課程ぐらいの院生とかも「尺度使った研究ってやばいよね」とかいっちゃう。なにがやばいのだろう。

というわけで、何がやばいのか考えてみたいのだけど、実は多くの人が心配するようなところや疑問に思うところは、それなりに理屈があったりもするので、まずはそこを擁護しつつ、批判的にリッカート尺度を使った研究について考えてみたい。

 

尺度水準の話

最初は、尺度水準の話。心理学を学ぶ学部や学科の学生は、尺度水準のことを最初に習う。Stevensの尺度水準も話がほぼ確実に出てくるのだが、教科書に書いてあることはイマイチ何を言ってるのかよくわからない。というわけで、簡単に尺度水準の話をまとめておこう。

測定するとはどういうことなのか、というのはいろいろ難しい議論があるけど、ここでは簡単に、測定とは、真の値を尺度得点に写像する関数であると考えてみよう。たとえば、真の値が0から1の範囲をとる実数だとする。このとき尺度は、それを別の値に変換するものであると考えればいい。たとえば0~0.1に1を、0.1~0.2に2を、0.0~0.3に3をに、という感じで。ここでどういう変換ルールについて分類したのが、尺度水準である。

ちょっと議論がややこしいので、とりあえず尺度水準は雑に言えば、真値→尺度値の変換方法のタイプ分けである。ただ、これは実際には正確ではないので、正確なバージョンはあとに書く。

尺度の4水準を、変換の規則ごとに分ける。なお、φ(x)は真の値xに対する尺度値を意味する。

絶対尺度：φ(x)=xである変換　つまり、真の値と尺度値のが同じ。心理では使わない。

比率尺度：変換がφ(x) = αx、ただしα>0、つまり、正の値をかけても意味が変わらない変換方法の集合

間隔尺度：変換がφ(x) = αx+β　ただしα>0、つまり、正の線形変換をしても意味が変わらない変換方法の集合

順序尺度：変換が、φ(x) = f(x)、ただしf()は単調増加関数、つまり、大小関係が維持される変換方法の集合

名義尺度：変換が、φ(x) = f(x)、ただしf()は一対一対応関数、つまり大小関係を維持しなくてもいいが、同一性だけは区別できる変換方法の集合

正確バージョン

真値→尺度の変換について、同じタイプの変換の集合を考える。その変換方法間でさらに変換することができる関係性の規則の違いが、尺度水準の違いを意味する。たとえば温度を測るとき、真の熱量→温度計の値という変換を考えるとき、摂氏でも華氏も温度を測定する写像だが、摂氏と華氏間の関係は線形変換を除いて不変である（線形変換で摂氏と華氏を変えられる）。このような写像タイプの集合が尺度だ、というのがStevesの尺度の定義である。つまり上の規則は、真値から尺度値の変換ではなく、変換タイプ同士に当てはまる関係性、というのが正確な尺度の定義。でも言わんとしていることは上とだいたい同じと考えても多分問題ない。

さて、上の定義を文系向け（？）に4水準の説明をもう少し補足しておく。

比例尺度には原点がある、という説明がされることが多いが、真の値の0が尺度値においても厳密に0が変換されるということを意味している。重さがないものを測ったら0という数値が得られるような尺度が比例尺度ということである。また演算で割り算が許容されると言われるが、正確には尺度値の比が、真値の比と対応する、という意味である（10mは5mの2倍だが、真値でも２倍長い）。

間隔尺度は、足し算ができるが割り算や掛け算ができないと言われることがある。これは正確ではなく、間隔尺度は線形変換について不変（真値の情報が歪められない）なので、平均値や標準化は問題がない。ただ、尺度値の比は、真値の比とは対応しない。ただ、尺度値間の差の比は、真値の差の比と対応する（φ(x)=αx+βに照らして計算してみてほしい）。つまり、それが「等間隔である」ことの意味である（10mと5mの差と15mと10mの差は両方とも5mで同じだが、それは真値でも同じ）。

順序尺度は、大小関係だけが保存されている。つまり、真値の情報が尺度化の段階でかなり落とされていると言っていい。しかし、真値がどういう量であるかにあまり依存しないのもいい点で、たとえば心理量は真値において0、つまりその量が存在しないという解釈ができないことが多い。そのような（測度ではないようなよくわからない量）であっても、順序尺度は利用できる。たとえば序数効用なんかも理論上は測定できる。

 

リッカート尺度は何を測っているのか

話が長くなってきたが、リッカート尺度の話である。

リッカート尺度とは、何かしらの量について、何かしらの質問や命題を提示し、「全く当てはまらない」「やや当てはまる」「とても当てはまる」といったラベルのどれかに反応させて測定する方法である。その後に、「全く当てはまらない」は1、「やや当てはまる」は2、という得点化を行う。どう見ても順序尺度である。

順序尺度は大小関係のみを保存するのだから、線形変換さえもできない。よって、平均値や標準化は、もとの尺度の情報を歪めるはずである。なぜ順序尺度のリッカート尺度に対して、そういう処理を心理学者は行うのだろうか？

ここにはいくつかの理屈あり得る。まず、リッカート尺度は心理量を直接測っているのではない、というものである。たとえば体重計は重さを直接測っている（と思う）。身長計も長さを測っている（と思う）。しかし、心理尺度は心理量を直接測ってない（2回言った）。

たとえば態度測定法では、心理量である態度と、測定されたものである意見を区別する。リッカート尺度は、提示された命題、たとえば「煉獄さんは尊い」に対して、真であるか偽であるかについての意見を訪ねていると考える。意見は、ざっくりいえば表明された態度のことなので、態度を反映しているが観察可能なものである。僕が「煉獄さんは尊い」と口に出して言ったとき、それは意見を言っているのであって、態度そのものを口に出したわけではない。

観測可能な意見から、直接観測できない態度を推定するのが、態度測定法である（このとき、観測できるというのは雑に、五感で知覚できる、ぐらいに思ってもらったらいい）。観測できないものを推定するには、そこに態度→意見についての理論が必要になる。その理論を提供するのが、心理測定学（Psychmetrics)である。典型的なものに、項目反応理論、因子分析、などなどのモデルがある。

たとえば、力（Forth)という物理量はたぶん観測できない。しかし、長さと重さと時間という観測可能な物理量から、F=maという力学の法則を利用して、測定される（加速度ａは時間と長さの関数で表せる）。それと同じと言ったら多分怒られると思うが、考え方としては同じで、潜在的な量から観測可能な量へのモデルがあれば、「理屈上は」測定が可能ということになる。

一応、別の理屈も書いておく。まずリッカート尺度が測っているのは確かに態度であって、それが直接に順序尺度で測定されていると考える。このとき、単純増加関数で写像するとき、多大な情報損失が起こっている（連続値のはずの態度が5段階になってるわけだから）。そこで、尺度項目をたくさん測定することで、失われたであろう情報を数理モデルを使って補ってみよう、という理屈である。ただ、心理学者的には上の説明のほうが納得する・・・？

 

項目反応理論

項目反応理論は、順序尺度で測定されたテストの回答や、心理尺度の意見データから、潜在的な心理量（学力や態度）を推定する方法である。上の態度測定の文脈で言うなら、潜在的な態度から、意見が表明される理屈を提示する測定モデルである。

項目反応理論そのものについてはこの記事あたりを見てください。あるいは、この記事とか。

これらの方法を使うと、順序尺度で測られた意見データから、態度を推定することができる。理屈上は、推定された潜在得点が態度得点である、ということができる。これが心理測定なのだ、という考え方から、リッカート尺度で平均値を使うことの是非を考えてみよう。

いま、段階反応モデル（Graded Response Model; GRM）という、リッカート尺度データに対してよく使われる項目反応モデルを使って、パラメータリカバリをしてみよう。適当に項目パラメータと態度の真値を決めて、GRMに従って反応データの乱数をたくさん（200人分ぐらい）発生させる。このデータに対してGRMを使って今度はパラメータと態度を推定するということをやってみよう。また、生成されたデータから今度は尺度平均値を計算し、真値との相関を見てみよう。

GRMに基づいて乱数データを発生するRコードが以下。ここでは200人、20項目、5件法を仮定している。そこそこ一般的な測定状況だと思う。

 

次に、GRMを推定するStanコード

 

これらを使って真値と、GRMで推定した潜在得点や尺度平均値との相関を見てみよう。

走らせるRコードは以下。

 

まずはGRMと真値の散布図は以下のようになり、相関は0.97だった。

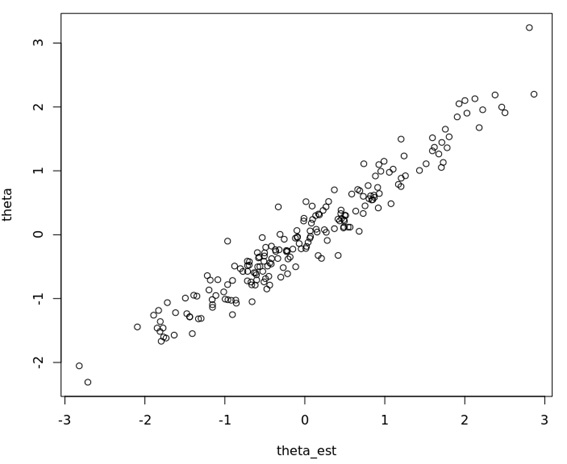
そこそこリカバリできている。

続いて、尺度平均値と真値の散布図。

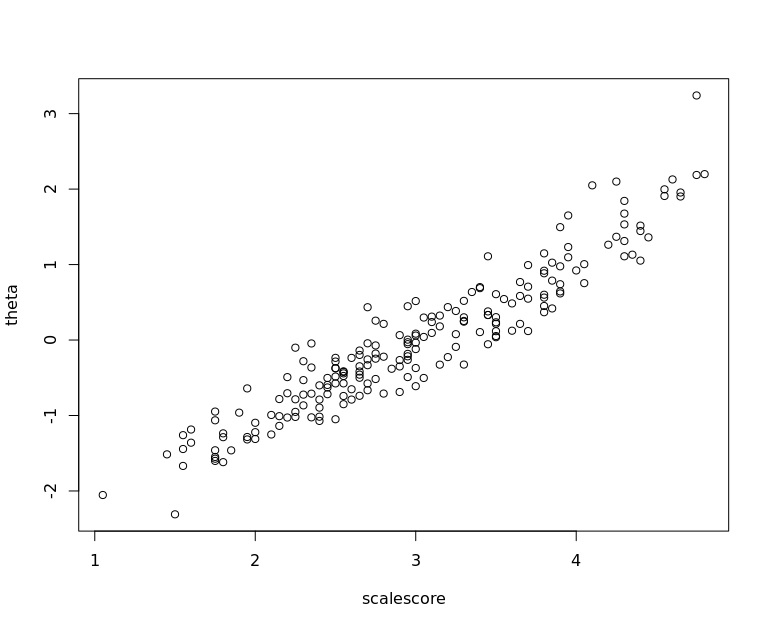
相関は0.94。そこそこ上手くリカバリできてしまっている。ついでに、GRMの推定値と尺度平均値の相関は0.98で、ほぼ同じ得点が得られている。

真値と推定値（GRMや尺度平均値）の相関は、項目数に依存する。そして、GRMと尺度平均値は何件法かに依存する。5件法ならほとんど1に近い相関が得られてしまう。

このようにリッカート尺度で得られた得点を平均化することは、理論上は確かにおかしいのだが、実用上ほとんど問題ないことがわかる。

なお、「因子分析は正規分布を仮定するのに使って大丈夫なの」問題も、上記とほとんど同じ論法で返事できる。正規分布に従ってようがなかろうが、十分なサンプルと項目数があれば真値（あるいはGRMで推定した結果）にほぼ一致する（ただしモデルが正しければ）。

 

なぜ尺度平均値を使うのか

GRMと尺度平均値がそこそこ一致するからと言って、尺度平均値を使うことの明確な理由にはなっていない。より正確であろうGRMを使うのがいいに決まっているのだから。

心理学者が尺度平均値を使う理由はたぶん、２つある。

１つは素朴な理由である。GRMとか使うの面倒くさい。

もう１つは、もう少し真面目な理由で、因子分析における因子得点ではなく、なぜ尺度平均値が使われるのかという話でよく説明される。

それは、因子分析やGRMで推定されるパラメータ（因子負荷量とか識別力）と、因子得点が同じサンプルで推定されているという問題である。サンプルが変われば、因子負荷量が変わってしまう。つまり、得点化方法がサンプルで異なることになる。これでは、同じ得点化といえないのではないか。比較ができないのではないか。という疑問が出てくる。

それに対して、尺度平均値は得点化の仕方はどのサンプルでも同じである。よって、研究間で得点の比較ができる。これは、計算機や統計モデルが十分発達してなかった時代には十分すぎる理由になったと思う。

現代では、項目反応理論で項目パラメータを大きいサンプルで推定して、個々の計算ではそのパラメータを使って推定すればいい。そうすればサンプルによる推定の違いや、サンプルサイズの小ささの問題などは気にしなくていい。

余談だが、昔卒論生が先行研究と因子構造が一致しない、と言ってきたことがある（というか卒論あるあるである）。元論文を見ると母集団はほぼ同じだが、サンプルサイズは１００程度である。こちらは４００。先行研究の因子構造のほうが怪しいはず。でも、先に論文化されたという理由でその因子構造が「正しい」と思われてしまうのは問題である。心理学研究などで採択される心理尺度作成論文はぜひとも、大きなサンプルサイズで因子分析をして、平均値と因子負荷量（できれば標準誤差も）を報告してほしい。そうすれば、卒論ではたとえサンプルサイズが１であっても同じ得点化方法で、同じ因子構造の因子得点を計算することができる。

 

 

他にもさまざまな議論がありえる

この記事では、リッカート尺度は順序尺度なのになんで平均化するのか？という問題について書いた。しかし、「自己評定式の心理尺度を使った研究が妥当なのか」という問については、ほかにもさまざまな問題に答えないといけない。

この記事では答えないが、問題の整理だけをしておこう。

自己評定式の心理尺度を使った研究で問題が起きうるとすれば、それは3つがあると思う。

1. 尺度水準の問題
2. 尺度構成法の問題
3. 構成概念の妥当性の問題

１．についてはこの記事で書いた。あとは２の尺度構成の問題と、３の妥当性の問題だ。

２はどういう問題かといえば、心理尺度でちゃんと心理量を測るための構成はどのようなものか？という問題。これは調査法とかの授業で習うと思うが、たとえばワーディングの問題、尺度順の問題、逆転項目の問題、ラベル数の問題、ラベルに何を使うのか問題、設問の仕方の問題、などなどがある。これらは、心理尺度についての本や、社会調査法についての本を見てもらえればたくさん検討されているのがわかると思う。これについてもまた時間があれば書こうと思う。

 

最も厄介なのは３の問題で、妥当性について。妥当性は、心理測定学でももちろんたくさんの議論があって半分は科学哲学に踏み込んだ議論もある。

心理学に関わらず、理論的構成概念（観測が直接できない構成概念）が実在するかどうかというのはさまざまな立場がある。経験主義にたてば、理論的構成概念なんてものは実在していないとなるだろう。実在論にもいろんな立場がある。

また、心理的な構成概念の実在性以外にも、尺度がそれを捉えていると言えるための証拠をどのように提示するべきかという議論がある。尺度の妥当性は証拠を示し続けることで担保されるのだという立場もある。あるいは、観測値と真値に因果的な連関がなければならないという立場もある。

僕の立場は、極めて反実在論に近い実在論である。つまり、態度のような心理的構成概念は、実在する。でもそれは自然種のようなものではない。社会種とかいったら怒られるか。でもそういうものだと思っている。これについては、いま共同研究で議論中なのでまとまったらどっかで発表します。