HAD18をアップしました。
久々のメジャーバージョンアップ!
今回の目玉機能はなんといっても「サンプルサイズ設計」です。
以下、追加機能一覧です。
- サンプルサイズ設計の機能を追加
- サンプリングシミュレーション機能を強化
- 「群ごと統計量」でCohenのd(記述統計と推測統計両方)を出力
信頼性革命以後の心理学研究において、検定を使う研究ではサンプルサイズの設計になにかしらの正当性を求められるようになりました。その一つの(そして最も典型的な)方法としてサンプルサイズ設計があります(これについてはまた別の日に記事でも書こうと思います)。HADではこのサンプルサイズ設計が誰でもできるレベルで簡単な操作性で搭載しました。多分、簡単。
それ以外に、これまでに合った機能をいくつか改良しました。基本的には心理統計教育をより効率化するための機能です。サンプリングシミュレーションは、特定の母数とサンプルサイズの設定で、乱数によって標本をたくさん出力する機能です。たとえば分散が1の母集団分布からサンプルサイズ30の標本を1万個シミュレーションする、という感じです。これによって、標本分散の平均が、母数よりも小さいこと、不偏分散の平均が母分散に非常に近くなることなどがすぐにわかります。また、t分布を仮定した危険率が5%付近に収まることなどを確認することができます。
群ごとの統計量は比較的にマイナーな機能ですが、群ごとの平均値、中央値などを出力する機能です。ここに、Cohenのd(標準化平均値差)を出力するようにしました。標準化効果量は別に推測統計学に特化した話ではないので、記述統計の文脈で学習できるように機能を追加しました。
以下では、サンプルサイズ設計の使い方を簡単に解説します。
◆サンプルサイズ設計のやり方
データシート(モデリングじゃないです)の一番下に、「検定力分析」というボタンが追加されました。これを押せば、以下のようなユーザーフォームが開きます。
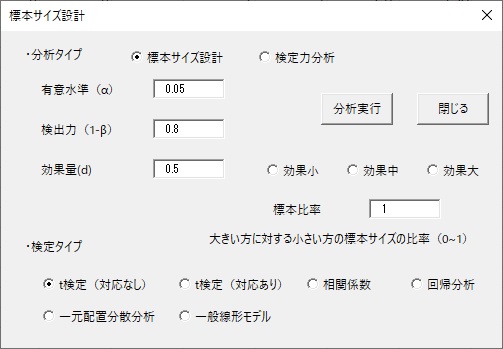
分析は、標本サイズ設計と、検定力分析を実行できます。基本的な使い方は同じなので、標本サイズ設計の方を解説します。
設計できる検定は、t検定、相関係数、重回帰分析、一元配置分散分析、一般線形モデルの5つです。
ではまず対応のないt検定のサンプルサイズ設計のやり方を解説します。
まず必要な情報は、1.有意水準、2.検出力、3.効果量の3つです。有意水準は心理学では5%が標準ですが、もちろんそれ以外の値でも設計可能です。検出力は80%がよく使われますが、追試のときなどは95%など、厳しめの設定にします。
効果量の見積もりは難しいですが、検出したい効果の大きさを入力します。効果量を小さく設定するほど、「こんなに小さな効果も検出したい」ということなので必要なサンプルサイズは大きくなります。つまり、効果量を小さく設定するほど「精度の高い検定を行う」ということになります。またt検定ではCohenのdを入力します。ここでは、Cohenで中程度とされている0.5を使います。
次に、右にある「標本比率」の設定です。これは、標本サイズが大きい方のグループに対して、小さい方のグループのサイズがどれくらいかを比で表したときの値を入力します。もし二つのグループが同じ標本サイズを考えているなら1を入れればOKです。
設定はこれで終わりです。簡単! あとは「分析実行」ボタンを押します。すると、
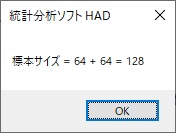
と結果が出ます。左が大きい方、右が小さい方のグループの標本サイズが表示され、その合計も出ます。
次に相関係数の場合もやってみましょう。
検定タイプを相関係数に変えると、効果量のところもrと表示されます。ここでは、「効果量小」ボタンを押してみます。すると、Cohenの基準で相関の小効果量の0.1が入力されます(あまり、Cohenの基準に頼りすぎるのもそれはそれで問題です。これはあくまで統計教育用の機能だと思ってもらえれば)。これで分析実行を押すと、標本サイズは779と計算されます。めっちゃいるやん!
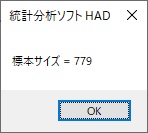
次は回帰分析です。回帰分析では、検定したい変数を含めていくつの説明変数が投入されているかの情報が必要です(それによって誤差の自由度が変わるので)。また回帰分析の効果量は、偏決定係数を入力します。これは、その変数を追加することで、これまで説明できていなかった分散のうち何%説明できるようになったかを表す指標です。イメージがつきにくい人は、分散分析でいう偏η2乗と同じだと思えばわかりやすいかも。あるいは、偏相関係数の2乗だと思ってもらってもいいです。ここでも0.1を入れてみました(ついでに0.1は結構効果が大きいです。
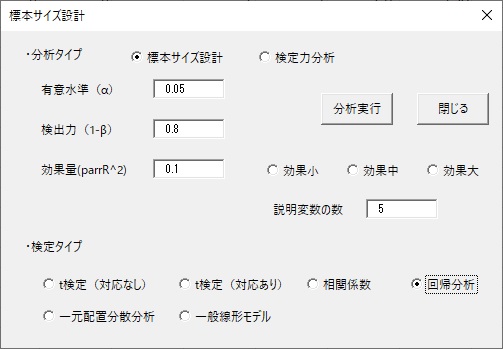
上の例では、説明変数を5にしています。設定はこれだけです。これで分析実行を押すと、125人と計算されました。
続いて、一元配置分散分析です。ここでは要因に含まれる水準の数を入力します。ここでは3水準の分散分析の設計をしてみましょう。
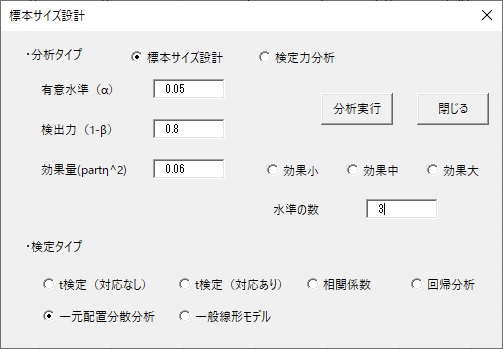
設定はこれだけです。分析実行をすると、次のように表示されます。
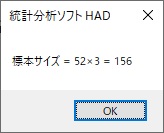
これは、各群の人数が52人で、全体で156人必要、ということです。このように一元配置分散分析では群ごとに等しい割り当てを前提に設計されます。
さて、最後に一般線形モデルの設計です。これ以上はちょっと設計がややこしいので別の記事に書こうと思います。一応、画面だけお見せすると・・・こんな感じ。

画面がでっかくなった! というわけで共分散分析を含んだ多要因計画の分散分析は、いろいろ設定しないといけないことが多いです。一要因参加者内計画もこちらで設計します。
◆検定力分析
検定力分析は、有意水準、効果量、そして標本サイズがわかっているときに、その検定がどれほど検出力があるか(帰無仮説が偽のときに何%の確率で正しく棄却できるか)を計算するものです。たとえば、ある実験をするときにリソース的に最大200人しか参加してもらえない場合、最大で検出力がいくらになるかを計算したいときに使います。
やり方は基本的に同じで、標本サイズのところに入力するだけです。

さて、以上がサンプルサイズ設計のやり方です。簡単でしょ? これなら学生にも教えられそうですよね。ぜひ、心理統計教育でお役立てください(もちろん皆さんの研究にも)。