HADでできる分析をまとめました。 マニュアルから抜粋してます。 HADはこちらからダウンロードできます。
分析方法一覧
HADでは以下の分析ができます。
データハンドリング
- 変数の作成 → 変数の平均、合計、逆転、尺度変換、値の再割り当てができます。
- 欠損値処理 → ペアワイズ削除とリストワイズ削除があります。
- フィルタ → 特定のサブジェクトを除外して分析できます。
- ラベルの表示→ 変数名以外にラベル、値ラベルを設定できます。
- グループごとの分析 → グループ別に分析を行います。
- 分析履歴の保存 → 分析の履歴を保存して,履歴から再分析が可能です。
データの要約
- 要約統計量 → 平均値や分散などの要約統計量を出力します。
- 箱ひげ図 → 変数の四分位統計量と箱ひげ図を出力します。
- ヒストグラム →変数のヒストグラムと分布に関する統計量を出力します。
- 度数分布表 → 変数の度数分布とヒストグラムを出力します。
- 正規性の検定 →コルモゴロフ・スミルノフ検定を行います。
- 一様性の検定 →等比率に対する適合度検定(χ2乗検定)を行います。
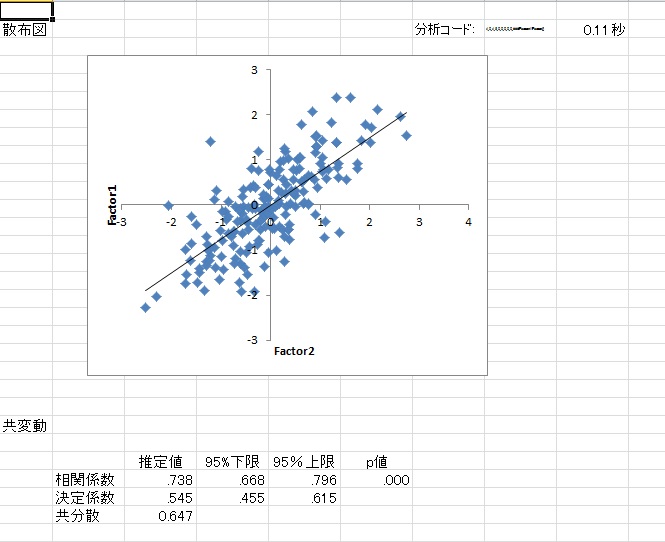
- 散布図 → 2変数の散布図を出力します。あと,直線への当てはまりを推定します。
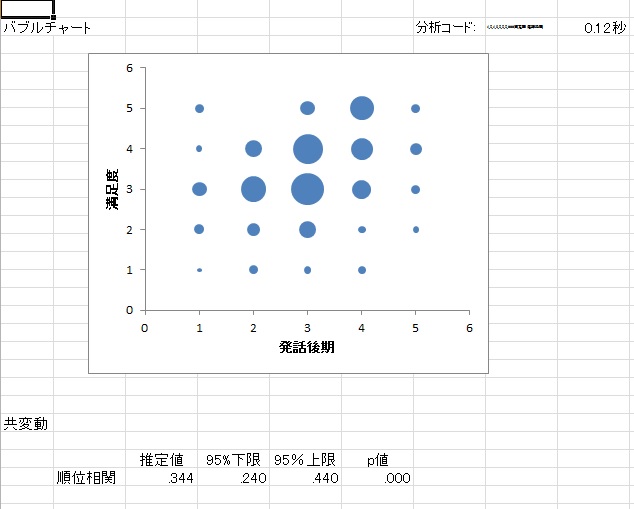
- バブルチャート → 2変数の順序尺度の散布図を出力します。
- クロス表 → 2変数のクロス表と連関係数,残差分析結果を出力します。
- 多重クロス表 → 5変数までの多重クロス表と対数線形モデルの結果を出力します。
差の検定
- 一標本の検定 → 一標本の平均値についてのt検定と区間推定を行います。
- 平均値の差の検定 → 対応あり・なしの場合の等平均値検定(t検定)を行います。
- 順位の差の検定 → 対応あり・なしの各種ノンパラメトリック検定を行います。
- 相関の差の検定 → 独立した2つのグループの相関係数の差を検定します。
- 等分散性の検定 →独立したグループの分散の差を検定します。
変数の関連性
- 相関分析 → 相関係数(偏相関係数)とその有意性検定を行います。
- 順位相関係数 → スピアマンの順位相関係数(偏順位相関係数)を出力します。
- カテゴリカル相関分析 → 順序データのパラメトリックな相関係数(ポリコリック,ポリシリアル相関)を計算します。
- 共分散 → 共分散行列を出力します。
- 項目分析 → α係数を計算し,尺度の項目分析を実行します。
- 信頼性係数 → 信頼性係数(α係数、Kappa係数など)を計算します。
- 主成分分析 → 複数の変数間を合成するための変数を推定します。
- 対応分析 → 2変数間の質的データの独立性検定と,対応分析を実行します。
データの予測(回帰分析系)
- 重回帰分析 → 重回帰分析を行います。
- 判別分析 → 判別分析を実行します。
- 多変量回帰分析 → 従属変数が複数の場合の回帰分析と正準相関分析を行います。
- 分散分析 → 5要因までの参加者内・間分散分析と多重比較を実行します。
- 順序回帰分析 → 順序ロジスティックあるいは順序プロビット回帰分析を実行します。
- 名義回帰分析 → 多項ロジスティック回帰分析を実行します。
- カウント回帰分析 → ポアソン回帰,負の二項回帰分析を実行します。
- トービット回帰分析 → 従属変数が打ち切りデータの場合の回帰分析を実行します。
- 二項回帰分析 → ある試行回数中の生起回数を予測する回帰分析を実行します。
- 混合分布回帰 → 回帰分析の当てはまりが異なる潜在的な母集団を推定します。
- 調整分析 → 上記の手法に対して,交互作用項の検定と,単純効果の検定を実行します。
- 媒介分析 → 上記の手法に対して, 媒介分析と間接効果の検定(ソベル検定・ブートストラップ検定)を実行します。
- 対数線形モデル → 多重クロス表における変数同士の関連性を推定します。
データの縮約(因子分析系)
- 主成分分析 →主成分分析を行います。
- 因子分析 → 因子分析と各種回転を実行します。
- 項目反応理論 → カテゴリカル因子分析と項目反応理論を実行します。
- 数量化分析 → 等質性分析(多重対応分析・数量化Ⅲ類)を実行します。
- 多次元尺度法 → 多次元尺度法を実行します。
データの分解(クラスタ分析系)
- 階層クラスタ分析 → 階層クラスタ分析(デンドログラム含)を実行します。
- 非階層クラスタ分析 →k-means法やその改良法を実行します。
- 混合正規分布モデル →連続データから複数の潜在的なクラスタを推定します。
- 潜在クラス分析 →名義データから複数の潜在的なクラスタを推定します。
- 潜在ランク分析 →潜在的な順序性のあるクラスタを推定します。
構造方程式モデル(潜在変数を含んだ因果関係の分析)
- 確認的因子分析 → 負荷する項目を仮説的に設定できる因子分析を実行します。
- 平均・共分散構造分析 → 潜在変数を含んだパス解析を実行します。
- 多母集団同時分析 → 複数グループを同時に分析します。
- 探索的因子分析 → SEMを用いて探索的因子分析を実行します。欠損値が含まれていても分析が可能です。
マルチレベル分析
- マルチレベル相関分析 →集団レベル・個人レベルの相関係数を算出します。
- ペアワイズ相関分析 → ペアワイズ相関分析を実行します。
- 階層線形モデル → 階層的データの線形モデルを実行します。
- マルチレベル構造方程式モデル → 階層データの構造方程式モデルを実行します。
- MUML用共分散行列 → AmosでマルチレベルSEMを実行するために使います。
- ペアワイズ共分散行列 → APIMを実行するのに使います。
- グループごとの回帰直線 →グループごとの回帰係数を計算し,グラフ表示します。
テキストマイニング
- TTM2HAD → TTMで分かち書きしたデータをHADに読み込んで,テキストマイニングを実行します。
行列演算
- 逆行列の計算 → 正方行列の逆行列を計算します。
- 行列式の計算 → 正方行列の行列式を計算します。
- 固有値分解(Jacobi法)→ 実対称正方行列の固有値と固有ベクトルを計算します。
- 固有値分解(QR法) → 正方行列の固有値を計算します(実部のみ)。
乱数によるデータ生成
- サンプリングシミュレーション →標本抽出の教育用ツールです。
- 一変量標準正規乱数 →標準正規分布に従う乱数を発生させます。
- 多変量正規乱数 →指定した共分散行列を母数とする正規乱数を発生させます。また,オプションで指定した共分散行列と完全に一致する正規乱数も生成できます。
HADのメインページに戻る 続きでは、図によるダイジェスト版(?)です。
HADの画面
HADのデータシートはこんな画面です。基本的にはエクセルなので、データの貼り付けや編集は簡単です。
モデリングはこちらのモデリングシートで行います。
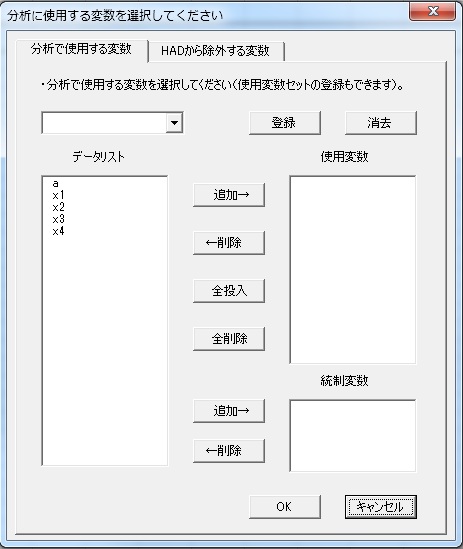
◆変数の指定 Ver9.5からGUIで選択できるようになりました。
得点を高群・低群のように2値化することも簡単。ダミー変数の作成もできます。
その他に、変数の合成やデータの標準化や中心化も実行可能。
◆変数情報の設定 値ラベルを指定することができます。
フィルタを指定して、分析から特定のサブジェクトを除外することができます。
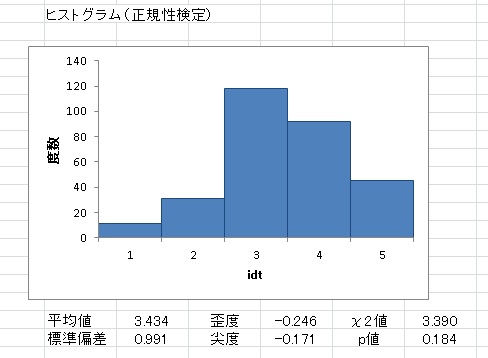
◆ヒストグラム
度数分布表と、それに対応したヒストグラムを作成。
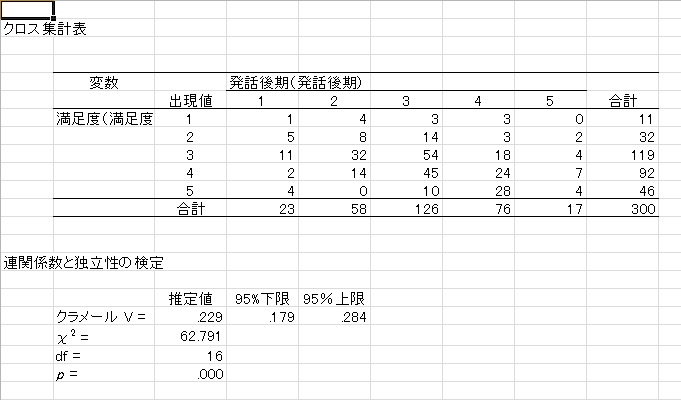
◆クロス表 2変数のクロス表と、連関係数を出力。
◆散布図とバブルチャート
連続変量の場合は散布図
順序尺度の場合はバブル散布図が便利
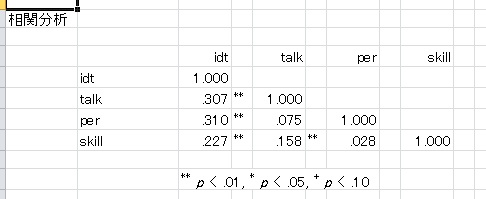
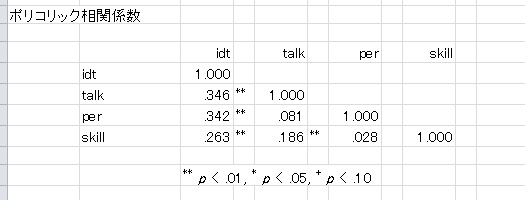
◆相関分析
ピアソンの相関係数のほかに、スピアマンの順位相関係数も計算可。
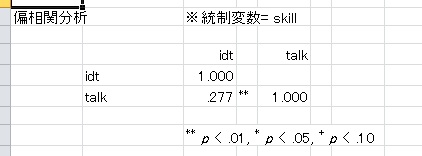
統制変数を指定すれば、偏相関分析も可能。
カテゴリカルデータの相関係数、ポリコリック,ポリシリアル相関係数も算出可能。
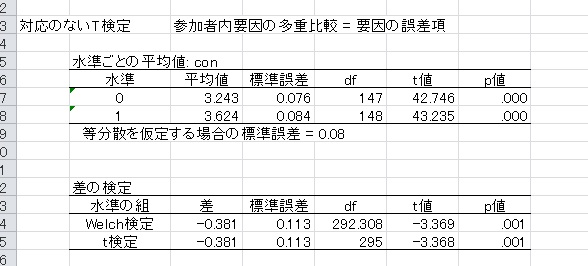
◆t検定
対応あり・なしのt検定を実行。等分散を仮定しないウェルチの検定も可能。
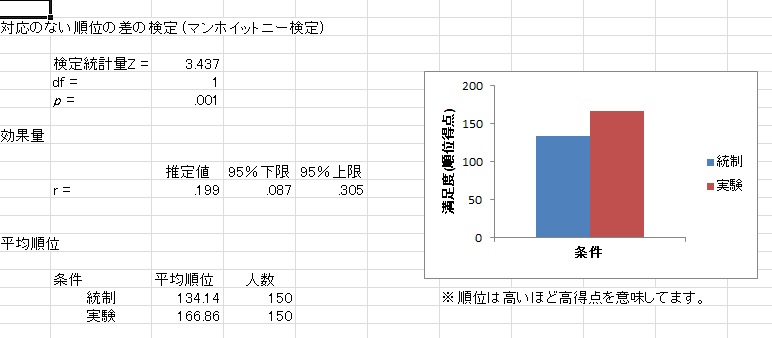
◆順位の差の検定(ノンパラメトリック検定)
マンホイットニーのU検定や、クラスカル・ウォリス検定、ウィルコクソン、フリードマン検定など、各種ノンパラメトリック検定も実行。3水準以上の場合は多重比較も行います。
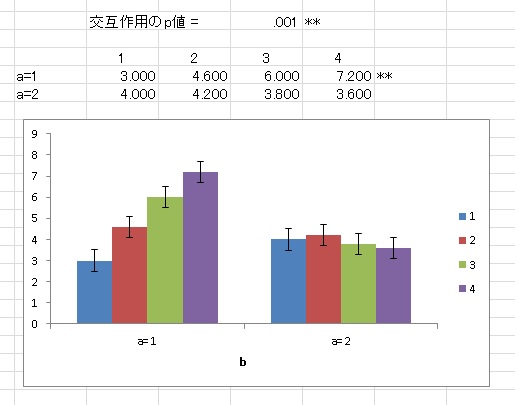
◆分散分析
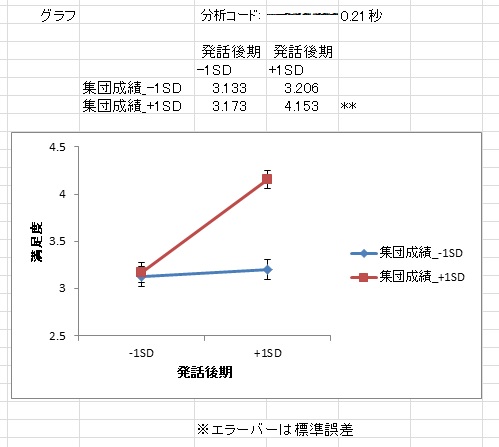
5要因までの参加者内・間計画を分析可能。多重比較も行います。 球面性の検定や効果量を出力 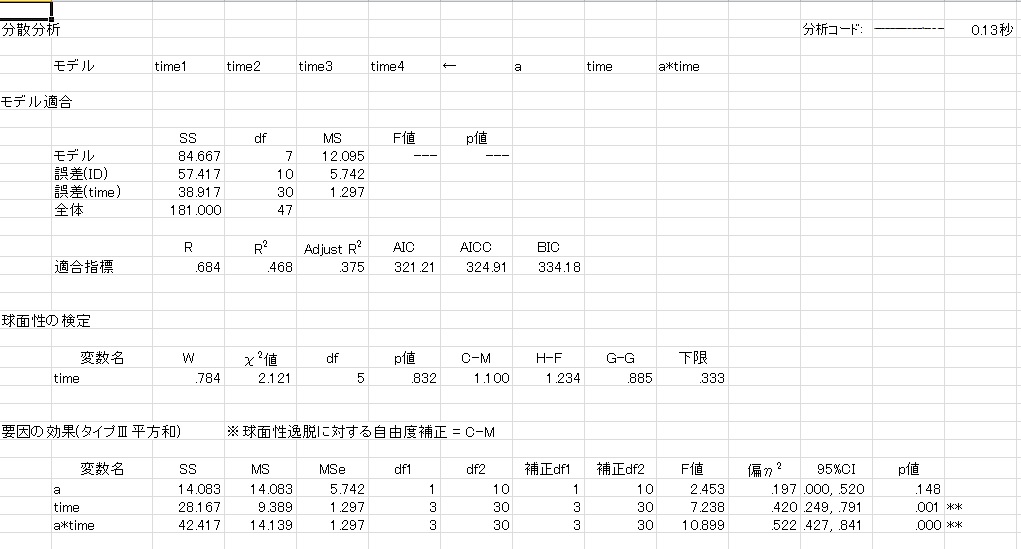
単純主効果のグラフ等も出力
◆階層的重回帰分析
回帰分析でステップに分けて効果を検討することが可能。
交互作用効果のグラフを出力。3要因交互作用まで可能。
◆ロジスティック回帰分析
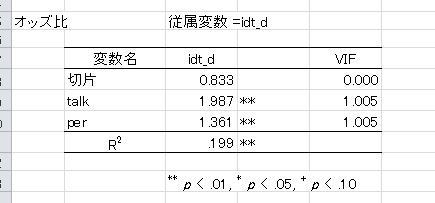
従属変数が順序や名義データの場合、ロジスティック回帰分析を実行可能。 ステップワイズ法や交互作用項を投入したモデルなどを検討できる。
また、オッズ比やグループ判別結果も出力します。
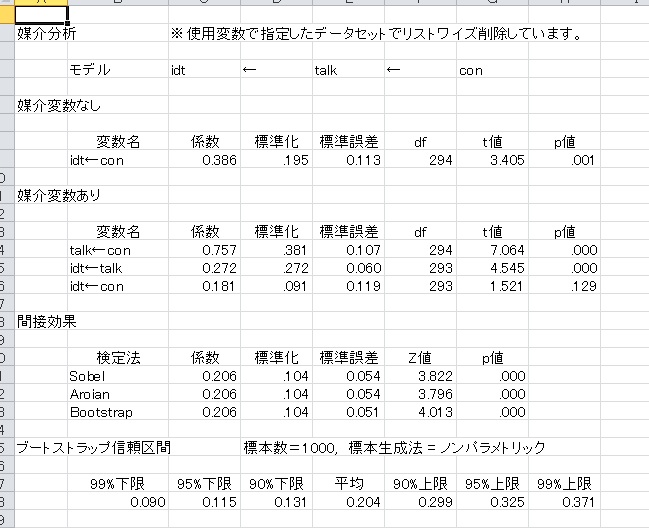
◆媒介分析
媒介分析の間接効果と検定、また、ブートストラップ信頼区間の計算が可能。
◆因子分析
最尤法、最小二乗法、反復主因子法,そしてカテゴリカル因子分析などの抽出法を選択可。回転はバリマックス、プロマックス、直接オブリミン、独立クラスタ、プロクラステス回転など。
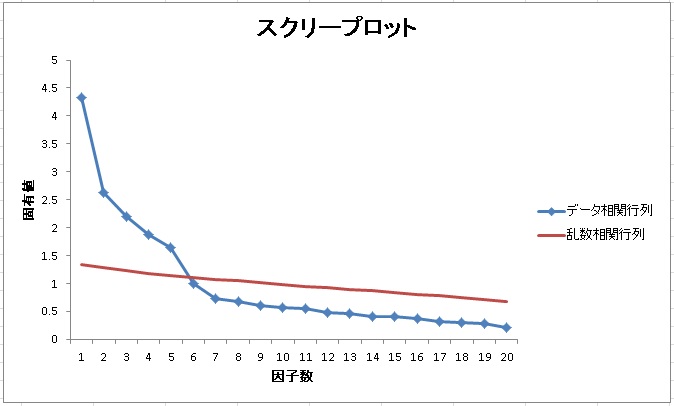
スクリープロットと平行分析 その他、MAPなどの因子数決定指標を出力。
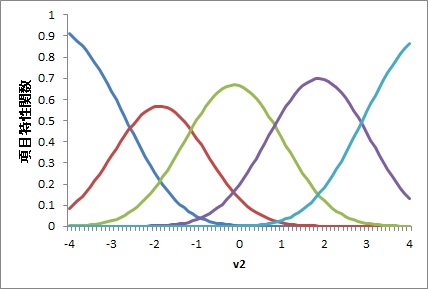
◆項目反応理論
カテゴリカル因子分析を一因子で実行すると,項目反応理論の出力が得られます。
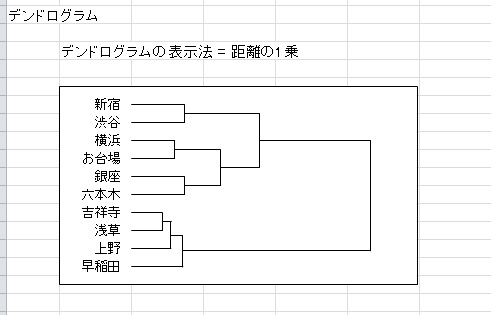
◆クラスター分析
ウォード法、群平均法、最近距離法、最遠距離法から選択可。 デンドログラムも出力
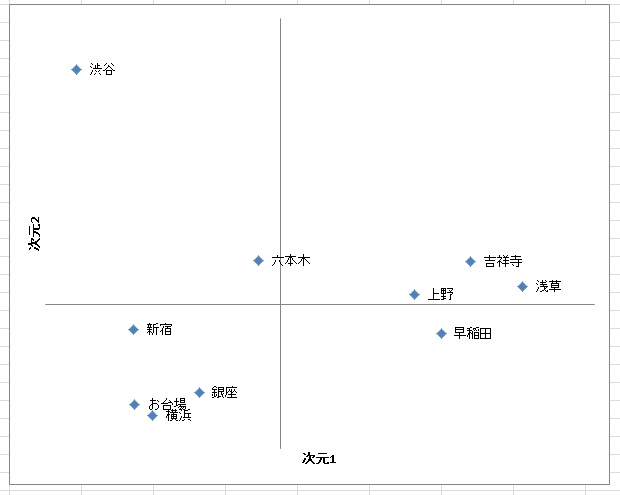
◆等質性分析(数量化Ⅲ類)
カテゴリデータを数量化し、2次元にマッピングします。
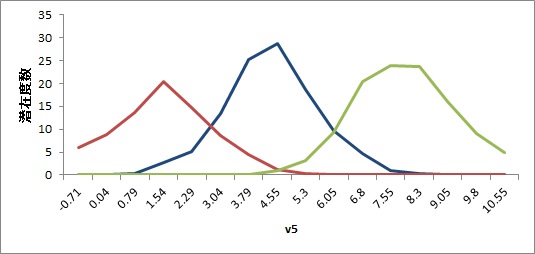
◆混合正規分布モデル
潜在的な正規母集団をデータから推定します。
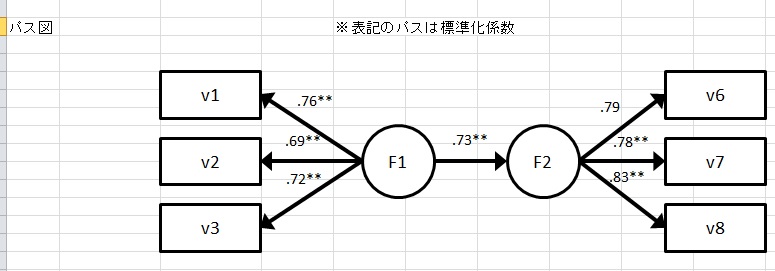
◆構造方程式モデル
潜在変数を含んだパス解析を実行します。
モデリングはパス図を描いて行うこともできます。出力も,描いたパス図に数値を出力することもできます。
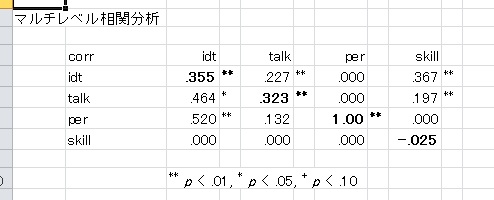
◆マルチレベル相関分析
級内相関係数とその有意性検定を出力。
以下の表は、対角が級内相関係数、上三角行列が個人レベル、下三角行列が集団レベル相関係数
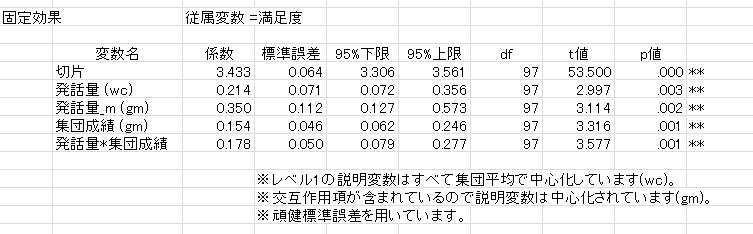
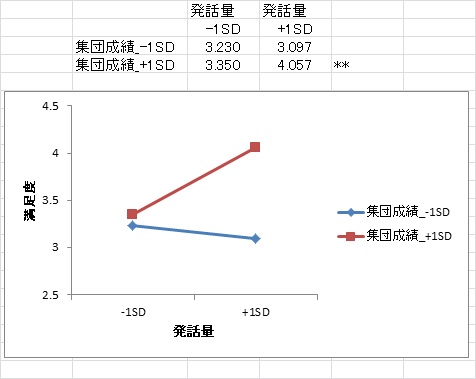
◆階層線形モデル(HLM)
グループ単位で測定されたデータを分析する,マルチレベル分析を実行できます。
重回帰分析と同様,レベル間交互作用効果と単純効果の検定が実行できます。
◆マルチレベル構造方程式モデル
構造方程式モデルを用いて,階層性のあるデータを分析します。
以上、「HADでできること」ダイジェスト版でした。