先日,HAD10.204をアップしました。そのときに新機能として搭載したのが,マハラノビス距離を用いた非階層クラスタ分析(以下,改良k-means法)です。
さて,この方法は,豊田・池原(2011;心理学研究)に掲載されたものです。従来のk-means法のアルゴリズムを改良して,より精度の高い手法となりました。アルゴリズムもとてもシンプルで,すぐにHADに実装できました。今回の記事は,この改良k-means法を紹介します。
k-means法ってそもそもなんぞや
最初に,k-means法について説明します。
クラスター分析には,階層クラスタ分析と,非階層クラスタ分析(SPSSでは大規模クラスタという名前)に分けることができます。
階層クラスタ分析は,クラスタに階層性を仮定しています。すなわち,下位のクラスタを統合して新しい上位のクラスタを作り,そのクラスタ同士をまた統合して・・・という感じに統合を繰り返し,最終的に一つのクラスタにします。その統合過程で,解釈しやすそうなクラスタ数を選ぶわけです。
クラスタ同士の距離の定義の仕方にいろいろな方法があり,「代表的な方法として,ウォード法,群平均法,最長距離法,セントロイド法などがあります。最近では,ほとんどウォード法か群平均法しか使われてないようですが。
非階層クラスタ分析は,クラスタの階層性を仮定せず,指定したクラスタ数にデータを分類します。その分類の仕方にいろいろ方法があり,最もシンプルかつよく使われるのがk-means法です。k-means法は,クラスタの中心点をクラスタに所属する個体の平均値とし,各個体ごとに,もっともクラスタ中心点に近いクラスタに移動していきます。どの個体も移動しなくなるまで繰り返し,収束したら終了です。
k-means法は計算スピードが速く,階層クラスタ分析にくらべて格段に計算が早く終わります。とくに,サンプルサイズが大きい場合(10万とか),階層クラスタはかなり時間がかかり,あまり現実的ではなくなります。その点,非階層クラスタ法であるk-means法は便利です(大規模クラスタと呼ばれる所以はここにあります)。
しかし,k-means法は初期値への依存度が非常に高く,また最適なクラスタ数を決めることができません。よって,分析するごとにクラスタの結果が変わる,という致命的な欠陥があります。
k-means法の改良版たち
このように,k-means法は便利だけど不便,という感じなので,さまざまな改良法が提案されています。
有名なのは,k-means++法で初期値をランダムにするのではなく,できるだけ散らばるように工夫したものです。
あとはx-means法というのがあり,最初に2つのクラスタをk-means法でわけ,それぞれの下位クラスタをさらにk-means法で2つに割って,というのを繰り返します。あとはBICなどの情報量基準で分割するのをやめるポイントを決めます。x-means法の改良版も提案されています(石岡, 2006)。
そして今回紹介するのが,豊田・池原(2011)のマハラノビス距離を用いたk-measn法です。
マハラノビス距離を用いたk-means法
従来のk-measn法は,距離をユークリッド距離として定義し,クラスタに分類していました。しかし,実際に分類に使う変数は強い相関関係があることも多くあります。
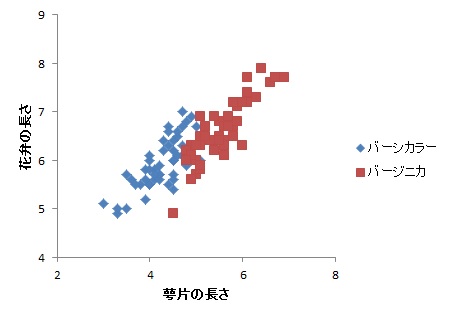
例えば,クラスタ分析のサンプルデータとして有名なアイリスデータは,花弁の長さと萼片の長さはかなり相関が高い(r=.81)です。そのような場合,単にユークリッド距離でクラスタリングするよりも,データの共分散を考慮した距離を用いたほうが適切であるといえます。
そこで,多変量正規分布を仮定した距離として,マハラノビス距離というのがあります。例えば,2変量データでアイリスの2種についてのデータを分類することを考えます。以下のような散布図になります。
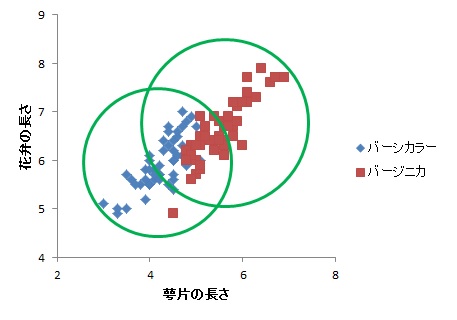
このとき,ユークリッド距離の場合,クラスタの中心から同心円状に距離を考えることになります。すると,下の図のように,かなり二つの種類がかぶってしまうことがわかります。
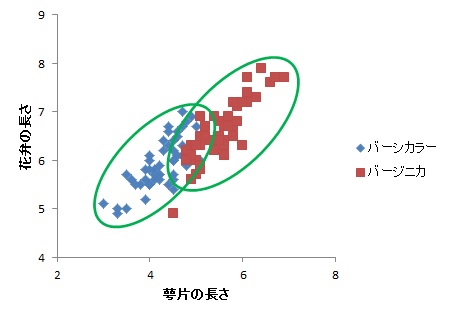
それに対し,マハラノビス距離を用いると,2変量間の相関関係を考慮した距離を考えるので,たとえるなら,以下のような楕円形で分類することができるようになります。
上の楕円形はもちろん恣意的ではありますが(笑),よりうまく分類できそうなことは伝わるかと思います。
また,マハラノビス距離は多変量正規分布上での距離なので,実は各個体がそのクラスタに所属する確率に変換することも簡単です。クラスタを所与とした場合の各個体のデータが得られる確率を尤度と言います。つまり,マハラノビス距離に基づくk-means法は,各個体ごとの尤度を最大にするようなクラスタ構造を推定する方法でもあるのです(実際はちょっとだけ違います)。
このように,変数間の関係性を考慮したk-means法は,クラスタごとに多変量正規性を仮定する混合正規分布モデルとも非常に近い推定方法でもあります。混合正規分布モデル,あるいは潜在混合分布モデルなどは,各クラスタへの所属確率を直接推定する方法ですが,マハラノビス距離を用いたk-means法は,所属確率(尤度)を距離とするような非階層クラスタ法であるといえます。
さらに,尤度を用いてクラスタリングするので,クラスタ数についてAICなどの情報量基準を利用できます。これによって,最適なクラスタ数を選択することもできるのです。便利!
改良k-means法でアイリスデータを分析してみる
アイリスデータ:3種類のアヤメ150個(50ずつ)について,4変量(花弁の長さ,幅,萼片の長さ,幅)から測定したデータです。
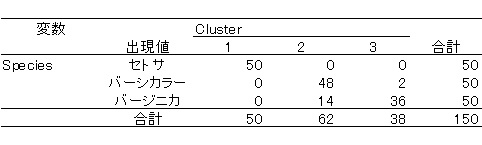
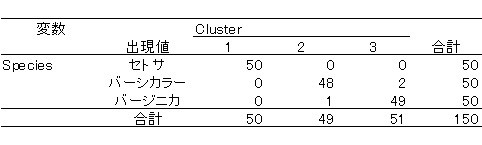
まずは普通のk-means法による分類です。HAD10.2の結果です。
上の表のように,セトサは100%分類できていますが,バーシカラーとバージニカの分類はイマイチです。
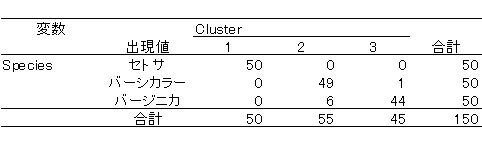
次に改良k-means法による分類を見てみましょう。同様に,HAD10.2の結果です。
普通の方法に比べて,かなり精度が上がっているのがわかると思います。
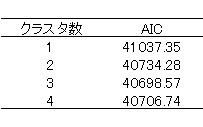
次に,AICの値から,クラスタ数がいくつが妥当なのか検討してみましょう。
上の表のように,クラスタ数が3の倍が最もAICが小さくなるのがわかります。
なお,潜在混合分布モデル(Mplus7で実行)による結果は以下の通りです。
上の表から,k-means法よりはうまく分類できていますが,改良k-means法のほうがより適切に分類できていることがわかります。
改良k-means法の欠点
改良されたとはいえ,いくつか欠点もあります。
・クラスタに所属する個体が2以上でないとマハラノビス距離が計算できない
・k-means法に比べて,やや計算時間がかかる
・初期値依存性が相変わらず高いので,何回か試して,最も尤度の大きい(情報量規準の小さい)ものを選択する必要がある(その分,計算時間もかかる)
といった点があります。
HADにおける改良k-means法
基本的には,心理学研究の載っているとおりにプログラムしたので,結果は再現するはずです。一応,初期値はk-means++法のように,多少初期値依存性を減らすようには工夫しています。ただ,エクセルで計算している限界もあり,計算に時間がかかることもあります。
もしこの方法を使ってみたい,という場合はHAD10.2以降をダウンロードしてください。
HADのダウンロードはこちらから。