HAD11.3から,欠損値のあるデータを分析できるようになりました。
この記事では,欠損値の処理と,その推定方法について簡単に書きます。ただ,この記事は数式とかそういう話はないので,詳しいことを知りたい方は村山航さんの記事(PDFが開きます)や,広大の徳岡君の資料などを参考にしてみてください。これらはとてもよくまとまっていて,わかりやすいです。
欠損値の3つのタイプ
欠損値が生じる要因として,大きく分けて3つが考えられています(細かく言えばもっとある)。
- データが,完全にランダムに欠損する
- データが,測定されている値に依存して欠損する(欠損データとは無関係)
- データが,欠損データに依存して欠損する
違いがちょっと分かりにくいですね。具体的に説明しましょう。
まず,データが完全にランダムに欠損するとは,データに反応しないのが,「たまたま」ということです。データになんにも依存していなくて,ほんと気まぐれ,という感じ。想定しにくいですが,一番わかりやすい欠損のタイプです。
問題は次の二つなんです。データが観測データの影響で欠損する,というのと,データが欠損データの値によって欠損する,という違い。ここで,観測データとは手元にあるデータ,測定できているデータのことです。そして欠損データとは,手元にはない,欠損してしまったけど測定していればこういう値だった,データです。すなわち,我々は欠損データがどのようなものかは具体的にはわかりません。
まず,後者の方がわかりやすいです。例えば体重を学校で測定するとして,「私,太ってるから体重はかりたくない。今日は休もう」と思ったとします。これは,その人の体重,つまり欠損してしまった体重の値に依存して欠損することになります。これが3つ目の,「欠損データの値によって」ということです。もしその人が学校に来て測れていれば,得られていただろうデータによって,欠損するかどうかが決まってしまっている場合が,このタイプです。
では二つ目は何かといえば,測定できているデータの影響で欠損する,ということです。これは体重だけではなく,ほかの変数であっても構いません。例えば体重を測定する場合,体重そのものではなく,性別に依存して学校を休む人がいたとしましょう。具体的には,体重に関係なく,女性だけが身体測定に欠席する,という場合。これは「他の観測されたデータによって」欠損が生じていることになります。つまり,その日学校を休んだ人の体重の値とはランダムに欠損しているけど,女性であるなら欠損しやすい,ということです。
少し補足を。この場合,女性のほうが体重が軽いから,体重と欠損には関連があるのでは?と思われるかもしれません。でも,性別を統制した場合に体重と欠損に関連がないのであれば,これは欠損データに依存していないことになります。つまり,たとえ欠損データと関連があったとしても,観測データによって欠損パターンが完全に説明できれば,「観測データに依存した欠損」と言えます。
この3つの欠損タイプには名前がついています。これらはよく出てくるので覚えておきましょう。
- 完全にランダムに欠損→Missing Completely At Random(MCAR)
- 観測データに依存する欠損→Missing At Random(MAR)
- 欠損データに依存する欠損→Missing Not At Random(MNAR)
欠損値データの対処法は,このタイプによって変わってきます。
MCAR(完全にランダムな欠損)の場合
MCARはランダムが偶然に起きているので,どのような対処をしても母集団への推定に影響しません。例えば,よく使われるペアワイズ削除やリストワイズ削除でも,母数の推定に影響しないのです。ただ,一つでも欠損があったら,全部のデータを使わないリストワイズ削除は,単純に「もったいない」です。データを測定しているのに,使わないということは,推定の精度が悪くなるからです。
次に考えられるのは,平均値代入などの単一の値を欠損値に代入する法です。これらの方法は,MCARであっても,推定値にバイアスを受けることがわかっています。また,推定精度を過剰によく推定しまうため,タイプⅠエラーを犯す危険性もあります。基本的には使わないほうがいいでしょう。
つまり,MCAR,完全にランダムな欠損なら,リストワイズ削除でもよい,ただし,もったいない,ということです。
MAR(観測データに依存して欠損)の場合
MARの場合は,リストワイズ削除でも推定にバイアスが生じることがわかっています。なぜなら,一部欠損した人の,欠損していないデータと関連があるため,その人のデータをすべて消してしまうと,特定の傾向を持つ人がデータからいなくなってしまうからです。
体重の例で言えば,女性が特に身体測定に休んだとすれば,不当に女性だけをデータから削除してしまうことになります。これでは推定に偏りが生じます。
ではどうすればいいかといえば,今のところ二つの解決法があります。
- 観測データをすべて用いた推定方法を使う
- 多重代入による推定を行う
さて,前者の「観測データをすべて用いた推定方法」とは,欠損したデータはわからないけど,それ以外のデータは全部使う,という方法です。これであれば,欠損は観測データのみに依存しているわけなので,偏りなく推定できることになります。
これを可能にする推定方法は,完全情報最尤法(Full Information Maximum Likelihood method)です。FIMLと呼ばれたり,ただ単に最尤法と呼ばれたりします。
最尤法は,最小二乗法のような推定方法の一種ですが,便利なことに,欠損データがあっても,それ以外のすべての情報を活用してモデルを推定できるのです。特に,SEMにこの推定法が用いられます。MplusなどはEMアルゴリズムという方法で欠損データを補完しながら尤度を最大化する方法が用いられています。HADは欠損パターンごとに尤度を計算する方法を使っています。
【追記:MCMCを用いたベイズ推定でも,FIMLと同じように,すべての情報を活用して推定ができます。】
次に後者の,多重代入法について。これは,ベイズ推定などで用いられるMCMC法を活用して,欠損値を様々な値で推定します。すると,たくさんのデータセットがいくつも作れることになります。この,たくさんのデータセットで何回も分析して(だいたい20~100ぐらい),たくさん算出された値の平均と分散を利用して推定します。これによって,一致性を保証しながら,欠損によるばらつきを推定精度に反映させることができます。
多重代入法を搭載しているソフトウェアも,だいぶ増えてきました。SPSSでも「Missing value analysis」というオプションを買えば実行できます。SASでも確かできるはず。Mplusでもできます。HADではできません。
さて,完全情報最尤法と多重代入法,どちらがいいのでしょうか。この二つの推定精度やバイアスはほぼ同程度だと言われています。なので,基本的にはどちらを使っても問題ないです。
完全情報最尤法のメリットは,特に何も考えなくても,ソフトウェアが普通に計算してくれる,という点です。また,乱数を使わないので,推定結果はどのソフトウェアでも一致します。一方,多重代入法は,乱数を使うので推定結果が一致しない,適合度が計算できないなど【追記:Mplusで普通に適合度が出せました。間違いです】の欠点があります。ただ,多重代入法のほうが少ない計算負荷でより良い推定ができる可能性があります(後述する補助変数が多い場合など)。適合度などが計算できるようになれば,多重代入法のほうが将来的には使われる可能性もあります。
MNAR(欠損データに依存して欠損)の場合
MNARの場合は,実は有効な方法はありません。FIMLや多重代入法でも,バイアスが生じてしまいます。また,どういうときがMNARなのかも,判断が難しいです。なぜなら,欠損データは我々は手に入れようがないからです。
ただ,MNARを極力MARに近づけていく方法があります。それは,観測データをたくさんとって,分析に反映させることです。上で述べたように,仮に欠損データと欠損パターンに関連があったとしても,観測データで欠損パターンを説明しきれば,それはMARと判断できます。つまり,欠損に関連しそうな変数をすべてモデルに入れてしまえばいいのです。そういう変数を補助変数と呼びます。
補助変数は,欠損パターンを予測するためだけに使われるので,実際に報告したいモデルに登場させる必要はありません。観測変数と共分散を仮定するだけなので,モデルの適合度などには影響しないのです。Mplusなどは補助変数を簡単に導入するためのオプションがあります。
このように,補助変数をたくさん入れてやれば,仮にMNARであっても,限りなくMARに近い状況に近づけてやることはできるわけです。
実データで試してみよう
では,わかりやすいように実際のデータでそれぞれの推定法を試してみましょう。ここで試すのは,リストワイズ削除と完全情報最尤法です。
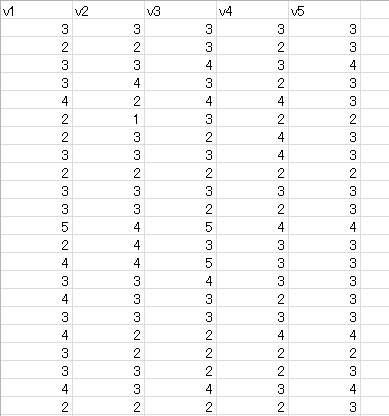
以下のような5変数のデータ一因子の因子分析をやってみます。これは完全データです。
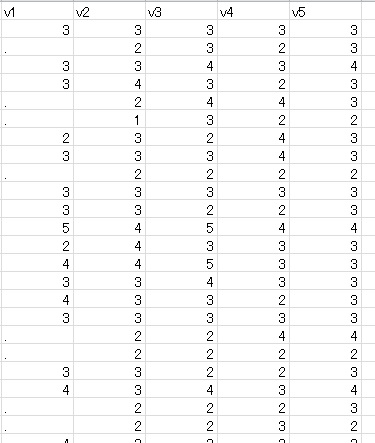
次に,下のように,v1をv2の値に依存させてに欠損させてみます。具体的には,v2の値が1か2の場合に欠損,それ以外は観測,という感じです。これは典型的なMARです。欠測は,200人中44人です。1/4が欠損していることになります。
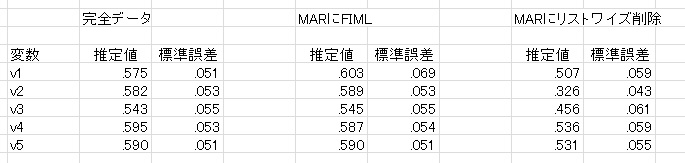
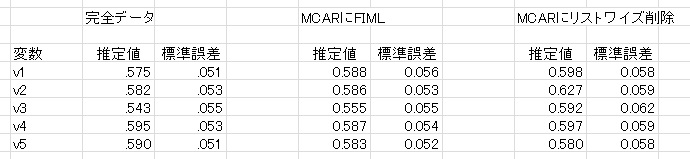
これらのデータを使って,HADで確認的因子分析をしてみました。結果は次のようになりました。なお,推定しているのは因子負荷量です。
完全データとFIMLは結構近いことがわかります。欠損が44もあるのに,v1の推定結果はそれほど影響を受けていません。また,欠損がない変数については,かなり完全データと近いのがわかります。標準誤差も,v1のみ悪く,それ以外はほぼ同じです。
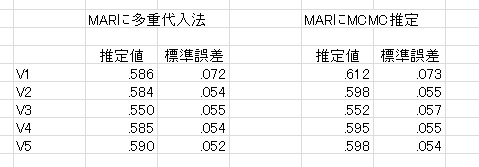
【追記:多重代入法とベイズ推定の結果も載せておきます。参考程度に。】
一方,リストワイズ削除の場合,v1も悪いですが,v2もかなり悪いです。これはv2に依存してv1を欠損させているからで,v2は1と2が全部消えているので,全然違う結果になります。また,リストワイズ削除はサンプルサイズが200-44の156となっているので,FIMLより標準誤差も大きくなります。
次に,欠損を完全にランダムにした場合(同じくv1から44人を欠損)の結果です。この場合だと,リストワイズ削除でもそれほど大きな影響は受けていません。ただ,FIMLのほうが標準誤差が小さいのがわかると思います。つまり,MCARでもFIMLのほうが良いことがわかります。
結論
さて,欠損タイプについて3つ説明しました。MCAR(完全にランダム),MAR(観測データに依存),そしてMNAR(欠損データに依存)があったわけですが,結局どうすればいいのでしょうか。
誤解を恐れず言えば,どのような場合でもとりあえず完全情報最尤法(あるいは多重代入法)を使えばいい,ということになります。もしMNARかもしれないなら,補助変数をたくさん(なんなら,とった変数全部)いれてやればよいです。推定に時間はかかりますが,バイアスは小さくなるはずです。たとえMCARであっても,FIMLや多重代入法のほうが,リストワイズよりも推定精度は高いです。つまり,より良い推定ができます。
これはSEMにだけ当てはまる話ではありません。たとえば回帰分析,因子分析,なんなら分散分析でも同じことが当てはまります。回帰分析と因子分析はSEMで表現できますし(探索的因子分析もMplusやHADでFIMLが使えます),分散分析はMixedモデルでFIMLを利用できます。分散分析ができるということは,t検定でも(この場合対応がある場合だけですが)利用できます。
SPSSユーザーでもMissing value alnalysisを買えば,簡単に多重代入法が利用できます。多重代入法は分析法に依存しない点はメリットです。乱数を固定してやれば,同じ推定結果を得られますから,再現性という点についても実は特に気にする必要もありません。
というわけで,リストワイズ削除なんかやめて,どんどんFIMLや多重代入法を活用しましょう!