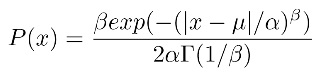誰得なのかよくわからない記事を書きます。※最後に追記あります
独立成分分析を調べていたら,ラプラス分布と正規分布の両方を含んだ「一般化正規分布」というのが出てきたので,調べてみました。
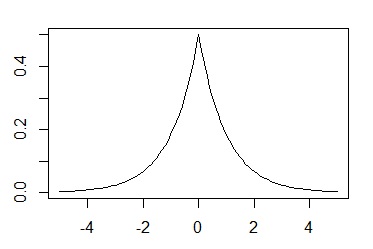
一般化正規分布は,平均μと,尺度パラメータα,形状パラメータβの3つのパラメータがあります。この分布の特徴は,左右対称の分布で,尖度を形状パラメータβで変えることができるというのが特徴です。βが1のときはラプラス分布,βが2のときは正規分布,βが∞のときはμ-αとμ+αの範囲の一様分布となります。
ついでに,ラプラス分布というのは,平均値あたりがすごいとんがっている分布です。
一般化正規分布。楽しそうですね。
しかし,Stanにこの分布は入っていません。なので前の記事の方法を使って,StanでMCMCできるようにしてみました。
まず,一般化正規分布の確率密度関数は次のようになります。
Γ()はガンマ関数です。
まず,Stanでfunctions{}ブロックに一般化正規分布の上の確率密度関数を書きます。関数名はggd_log()です。名前の通り,戻り値はlogしたものにします。また,Stanでは絶対値はabs()は推奨されて無くて,fabs()のほうがよいようです。イマイチ違いはわかってません。
|
1 2 3 4 5 6 7 |
functions{ //一般化正規分布を定義 real ggd_log(real y, real mu, real alpha, real beta){ real temp; temp <- beta * exp(-(fabs(y-mu)/alpha)^beta)/ (2*alpha*tgamma(1/beta)); return log(temp); } } |
あとは,この分布を使ってパラメータを推定するようなStanコードを書けばOKです。もちろん,x ~ ggd()というようにサンプリング関数として使えます。
下のコードでは,一般化正規分布の標準偏差をgenerated quantities{}で吐き出すコードも加えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
functions{ //一般化正規分布を定義 real ggd_log(real y, real mu, real alpha, real beta){ real temp; temp <- beta * exp(-(fabs(y-mu)/alpha)^beta)/ (2*alpha*tgamma(1/beta)); return log(temp); } } data{ int N; //サンプルサイズ real y[N]; //データ } parameters{ real mu; //平均値 real real } model{ mu ~ normal(0,100); //平均値の事前分布 alpha ~ cauchy(0,5); beta ~ cauchy(0,5); for(n in 1:N){ y[n] ~ ggd(mu,alpha,beta);//一般化正規分布を使う } } generated quantities{ real sigma; sigma <- (alpha^2*tgamma(3/beta)/tgamma(1/beta))^0.5; } |
それでは,正規乱数から生成したデータで推定してみましょう。なお,上のコードはfunction2.stanという名前で保存しています。
平均5,標準偏差2の正規乱数を1000個作り,推定してみました。
|
1 2 3 4 5 6 7 |
library(rstan) set.seed(123) y <- rnorm(1000,5,2) fit.normal <- stan("function2.stan",data=list(N=1000,y=y)) fit.normal |
結果は次のようになりました。
|
1 2 3 4 5 6 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu 5.03 0.00 0.06 4.91 4.99 5.03 5.07 5.15 1502 1 alpha 2.78 0.00 0.12 2.51 2.70 2.78 2.86 3.00 1048 1 beta 1.96 0.00 0.14 1.70 1.87 1.96 2.06 2.25 1029 1 sigma 1.99 0.00 0.04 1.90 1.96 1.99 2.02 2.08 3512 1 lp__ -2103.35 0.03 1.18 -2106.28 -2103.89 -2103.07 -2102.48 -2102.00 1291 1 |
ほぼmu=5.03,σ=1.99とほぼ母数通りとなりました。またβは1.96となり,2に近い値が推定されました。
次にラプラス分布を生成してみます。
ラプラス分布をして推定してみます。パラメータは平均μと尺度パラメータφです。φは一般化正規分布のαと同じです(たぶん)。
|
1 2 3 4 5 6 7 8 9 10 |
rlaplace <- function(n,mu,phi) { u <- log(runif(n)) v <- ifelse(runif(n)>1/2, 1, -1) return(u*v*phi+mu) } set.seed(123) y <- rlaplace(1000,5,2) fit.laplace <- stan("function2.stan",data=list(N=1000,y=y)) fit.laplace |
推定した結果が以下です。
|
1 2 3 4 5 6 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu 5.01 0.00 0.07 4.87 4.96 5.01 5.05 5.14 1189 1 alpha 2.06 0.01 0.18 1.72 1.93 2.05 2.18 2.42 1283 1 beta 1.02 0.00 0.06 0.91 0.98 1.01 1.06 1.14 1232 1 sigma 2.85 0.00 0.10 2.67 2.78 2.84 2.91 3.06 3237 1 lp__ -2393.61 0.04 1.28 -2396.77 -2394.19 -2393.26 -2392.67 -2392.19 934 1 |
μもαも母数に近い値となっています。βは1.02と,ラプラス分布の値とほぼ一致しています。
最後に一様分布です。0から2の範囲の一様分布から1000個生成しました。
|
1 2 3 4 |
set.seed(123) y <- runif(1000,0,2) fit.uniform <- stan("function2.stan",data=list(N=1000,y=y)) fit.uniform |
結果は,以下です。
|
1 2 3 4 5 6 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu 1.00 0.00 0.00 0.99 1.00 1.00 1.00 1.00 1173 1.00 alpha 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.01 1388 1.00 beta 372.62 27.52 417.58 83.57 162.74 240.31 396.72 1607.67 230 1.01 sigma 0.58 0.00 0.00 0.57 0.58 0.58 0.58 0.58 979 1.00 lp__ -698.25 0.04 1.29 -701.62 -698.83 -697.90 -697.33 -696.82 859 1.00 |
μが1でαが1なので,0~2の一様分布として推定できているのがわかります。また一様分布の場合βは∞となりますが,今回は372と推定されています。十分大きい値なのでだいたいOKという感じでしょうか。
このように,一般化正規分布は,ラプラス~正規~一様分布という3つの分布がβという形状パラメータで連続的に表現される楽しい分布でしたとさ。
追記
beroberoさんから,確率密度は最後のlogとるんじゃなくて,最初からできるだけlog使って計算したほうが速いよ!というご指摘をもらいました。
@simizu706 恐らく最後にlog(temp)とするより、可能な限りlogをはじめにとって、log(beta) - (fabs(y-mu)/alpha)^beta - log(alpha) - lgamma(1/beta)を返した方が安定で高速と思います!
— Kentaro Matsuura (@berobero11) 2016年6月2日
というわけでご指摘にようにコードを修正してみました。
|
1 2 3 4 5 6 7 |
functions{ //一般化正規分布を定義 real ggd_log(real y, real mu, real alpha, real beta){ real temp; temp <- log(beta) -(fabs(y-mu)/alpha)^beta - log(alpha)- lgamma(1/beta); return temp; } } |
すると,改善前のコードだと,13秒かかってたのが8.5秒と,かなりスピードアップしました。というわけで,こっちのほうがオススメです。