Stanのアドカレ,盛り上がってますね。
さて,今日(2017年12月11日)のアドカレ記事は山口大学の小杉さんでした。
結論としては「ブラマヨ」とのことでした。
そして,Twitterでこんな感じに煽ってました。
データも公開してますので、結果に納得のいかない人は再分析してみてね! https://t.co/7POC81w4dE
— kosugitti (@kosugitti) 2017年12月10日
じゃあ僕も再分析やって見るか,という勢いだけの記事です。
小杉モデルを確認
小杉さんのモデルは,採点者の「採点のばらつき」をモデリングしています。ある漫才への評価は,その漫才師の漫才力に,評価のばらつきが加味されているだろう,というわけです。
確率モデルは
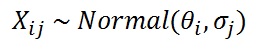
で,漫才師iが,採点者jに採点されたときの得点Xは,漫才力θを平均,採点者のバラ付きσを標準偏差とした確率分布に従うだろう,というわけです。
ここで僕はちょっと違うモデルを考えてみます。
採点者の変量効果を推定する
小杉さんのモデルで不満点があるとすれば,採点者の甘さが考慮されてないところです。例えば上沼恵美子は全体的に甘いけど,博多大吉は厳しい,とかです。このように採点者の採点の甘さが正規分布に従うような階層モデルを考えてみます。
まず,採点結果は,全体平均+漫才力+採点者の甘さを平均とした正規分布に従うとします。漫才力,採点者の甘さは平均0の正規分布に従うと仮定します。ただ,分散は推定します。
つまり,
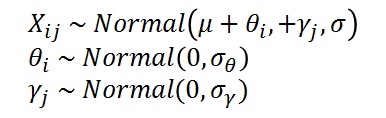
という確率モデルになるわけです。
Stanコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
data{ int int int int idX[L]; //player ID index int idY[L]; //rator ID index real X[L]; // scores } parameters{ real mu; vector[N] manzai; vector[M] saiten; real real real } model{ //likellihood for(l in 1:L){ X[l] ~ normal(mu + manzai[idX[l]] + saiten[idY[l]],sig); } //prior manzai ~ normal(0, sig_manzai); saiten ~ normal(0, sig_saiten); sig_manzai ~ cauchy(0,5); sig_saiten ~ cauchy(0,5); sig ~ cauchy(0,5); } |
これを"m1_shimizu.stan"と適当に名前をつけてStanを走らせてみましょう。読み込むデータ自体は小杉さんのブログ記事と全く同じです。
Rコードは以下です。
|
1 2 |
model.shimizu <- stan_model("m1_shimizu.stan") fit.shimizu <- sampling(model.shimizu,data=datastan,iter=2000,chains=2,cores=1) |
結果は次のような感じ。
まずは漫才力の結果です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat manzai[1] 0.07 0.04 1.91 -3.67 -1.18 0.02 1.33 3.72 2000 1.00 manzai[2] -8.85 0.04 1.88 -12.37 -10.12 -8.82 -7.55 -5.18 2000 1.00 manzai[3] 3.78 0.03 1.43 0.98 2.81 3.82 4.72 6.59 2000 1.00 manzai[4] -4.00 0.04 1.25 -6.49 -4.84 -3.99 -3.16 -1.59 776 1.01 manzai[5] 1.23 0.05 1.84 -2.33 0.01 1.22 2.42 4.87 1518 1.00 manzai[6] 2.25 0.05 2.04 -1.82 0.91 2.26 3.61 6.27 2000 1.00 manzai[7] -5.70 0.04 1.81 -9.32 -6.86 -5.73 -4.50 -2.35 2000 1.00 manzai[8] -6.38 0.03 1.25 -8.82 -7.24 -6.37 -5.56 -4.00 2000 1.00 manzai[9] 4.22 0.04 1.49 1.25 3.23 4.24 5.20 7.16 1215 1.00 manzai[10] 4.28 0.05 1.86 0.53 3.09 4.25 5.52 7.86 1461 1.00 manzai[11] -8.69 0.04 1.45 -11.56 -9.70 -8.73 -7.71 -5.86 1181 1.00 manzai[12] -2.33 0.04 1.87 -6.04 -3.62 -2.33 -1.05 1.33 2000 1.00 manzai[13] 4.22 0.05 1.91 0.38 3.00 4.23 5.49 7.79 1445 1.00 manzai[14] 1.80 0.05 1.50 -1.17 0.78 1.78 2.81 4.85 1101 1.00 manzai[15] -2.08 0.04 1.25 -4.57 -2.90 -2.11 -1.25 0.34 994 1.00 manzai[16] -2.41 0.04 1.85 -6.00 -3.65 -2.46 -1.16 1.22 2000 1.00 manzai[17] -1.86 0.04 1.90 -5.47 -3.16 -1.91 -0.57 1.88 2000 1.00 manzai[18] -1.91 0.04 1.89 -5.58 -3.14 -1.90 -0.67 1.84 2000 1.00 manzai[19] 2.90 0.04 1.86 -0.86 1.63 2.88 4.12 6.57 2000 1.00 manzai[20] 2.49 0.05 2.05 -1.40 1.07 2.50 3.85 6.61 1393 1.00 manzai[21] 4.26 0.04 1.93 0.52 2.97 4.21 5.56 8.05 2000 1.00 manzai[22] 2.98 0.04 1.23 0.61 2.13 2.97 3.81 5.38 811 1.00 manzai[23] 4.07 0.04 1.25 1.61 3.23 4.08 4.91 6.49 988 1.00 manzai[24] -6.17 0.05 1.44 -9.04 -7.12 -6.16 -5.18 -3.34 790 1.00 manzai[25] 2.99 0.03 1.52 -0.01 1.92 3.02 4.02 5.99 2000 1.00 manzai[26] -0.91 0.04 1.44 -3.68 -1.89 -0.96 0.10 1.82 1032 1.01 manzai[27] -7.18 0.04 1.87 -10.66 -8.46 -7.18 -5.94 -3.45 2000 1.00 manzai[28] -0.76 0.04 1.40 -3.43 -1.67 -0.81 0.18 2.13 1055 1.00 manzai[29] -0.03 0.04 1.89 -3.83 -1.32 0.02 1.26 3.55 2000 1.00 manzai[30] -2.43 0.04 1.24 -4.76 -3.30 -2.41 -1.58 -0.01 917 1.00 manzai[31] -6.67 0.04 1.86 -10.41 -7.90 -6.68 -5.45 -2.90 2000 1.00 manzai[32] 0.20 0.04 1.23 -2.29 -0.62 0.20 1.03 2.53 942 1.00 manzai[33] 3.55 0.05 1.81 -0.03 2.33 3.54 4.81 7.11 1388 1.00 manzai[34] 4.79 0.05 1.82 1.23 3.54 4.78 6.01 8.35 1343 1.00 manzai[35] 2.73 0.04 1.24 0.35 1.92 2.72 3.56 5.15 1003 1.00 manzai[36] 1.32 0.04 1.13 -0.85 0.57 1.27 2.09 3.54 725 1.00 manzai[37] -5.56 0.04 1.44 -8.39 -6.56 -5.52 -4.56 -2.84 1090 1.00 manzai[38] -1.47 0.03 1.42 -4.21 -2.44 -1.47 -0.45 1.21 2000 1.00 manzai[39] 5.92 0.03 1.46 3.06 4.93 5.91 6.90 8.81 2000 1.00 manzai[40] 1.86 0.05 1.91 -1.85 0.58 1.89 3.20 5.56 1426 1.00 manzai[41] 1.46 0.04 1.11 -0.71 0.71 1.49 2.21 3.59 812 1.00 manzai[42] 5.09 0.05 1.84 1.58 3.86 5.09 6.30 8.81 1275 1.00 manzai[43] -0.45 0.03 1.42 -3.20 -1.42 -0.45 0.51 2.39 2000 1.00 manzai[44] 0.45 0.04 1.90 -3.20 -0.86 0.47 1.74 4.17 2000 1.00 manzai[45] 5.30 0.05 1.87 1.74 4.04 5.30 6.56 8.92 1194 1.00 manzai[46] 0.88 0.05 1.84 -2.71 -0.38 0.90 2.12 4.44 1248 1.00 manzai[47] -0.10 0.03 1.46 -2.94 -1.08 -0.07 0.89 2.66 2000 1.00 manzai[48] 2.64 0.04 1.80 -0.78 1.44 2.64 3.82 6.07 2000 1.00 manzai[49] -0.43 0.05 1.82 -3.93 -1.65 -0.44 0.80 3.19 1352 1.00 manzai[50] -0.83 0.05 1.82 -4.45 -2.02 -0.82 0.38 2.65 1590 1.00 manzai[51] 3.74 0.04 1.31 1.12 2.83 3.74 4.65 6.27 852 1.00 manzai[52] 2.72 0.04 0.84 1.04 2.17 2.74 3.29 4.36 527 1.00 manzai[53] -4.36 0.04 1.12 -6.50 -5.12 -4.34 -3.60 -2.19 759 1.00 manzai[54] 0.74 0.05 2.07 -3.26 -0.71 0.72 2.15 4.80 1646 1.00 manzai[55] -0.18 0.06 1.95 -3.92 -1.51 -0.16 1.15 3.54 1243 1.00 manzai[56] -1.94 0.04 1.42 -4.60 -2.94 -1.95 -0.96 0.79 1087 1.00 manzai[57] -1.90 0.04 1.20 -4.28 -2.67 -1.90 -1.12 0.59 924 1.00 manzai[58] 0.45 0.05 1.74 -3.00 -0.76 0.43 1.63 3.73 1341 1.00 manzai[59] 1.47 0.04 1.80 -2.07 0.23 1.46 2.67 5.02 2000 1.00 manzai[60] -4.25 0.05 1.85 -7.97 -5.44 -4.24 -2.94 -0.66 1472 1.00 manzai[61] 4.69 0.04 1.26 2.30 3.80 4.69 5.52 7.20 888 1.00 manzai[62] -1.21 0.04 1.00 -3.15 -1.91 -1.17 -0.49 0.71 795 1.00 |
そこまでキレイに,というわけではないですが収束しています。
小杉さんにggplot2のコードを送ってもらったので,同じ図表を作ってみました。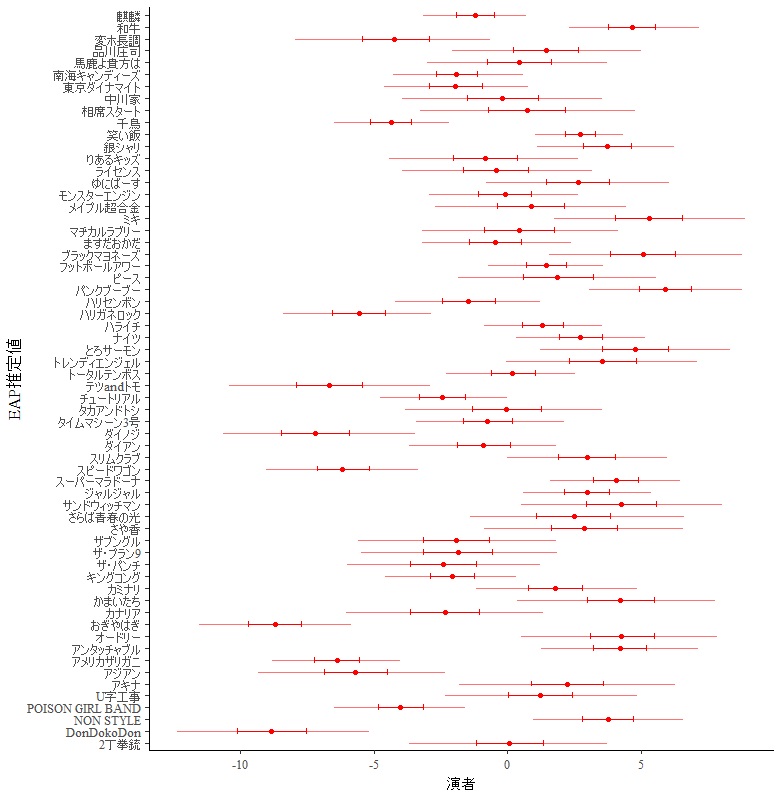
ちょっと見にくいですが,実は一番漫才力が高いのは,パンクブーブーという結果になりました。
続いて,採点者の「採点の甘さ」の推定です。
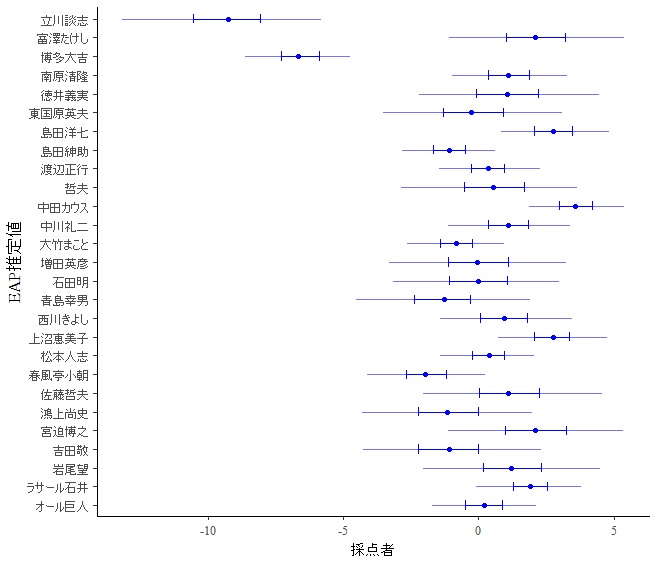
立川談志や博多大吉はかなり採点が厳しく,中田カウスなどは採点が甘いことがわかります。
なお,漫才力のSDと,採点の甘さのSDはあまり変わらなかったです。若干漫才力の分散のほうが大きいかな。むしろ,意外に採点の甘さの散らばりがでかいというべきか。また,全体平均は86.71点でした。
|
1 2 3 4 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu 86.71 0.06 0.88 84.98 86.12 86.66 87.29 88.45 237 1 sig_manzai 4.05 0.01 0.45 3.24 3.73 4.03 4.33 5.00 920 1 sig_saiten 3.09 0.01 0.53 2.19 2.71 3.03 3.41 4.26 1278 1 |
結論
小杉さんの記事ではブラマヨが最強,ということでしたが,採点者の甘さを考慮に入れるとパンクブーブーがトップとなりました。とはいえ,信頼区間がでかいので明確な違いがあるとは到底言えません。
なぜこのモデルではパンクブーブーが上回ったかといえば,もしかしたらブラマヨは甘い採点者がいるときに登場していたのかもしれません。
実際に見てみると,ブラマヨがでた2005年は,少し甘めのラサール石井がいている一方,パンクブーブーの年はいないみたいです。
このように,モデリングを変えると結果が微妙に違ってくることがあります。小杉さんのモデルは,同じ「小杉」がいるブラマヨに少し甘めのものになっていたと言わざるをえないでしょう。
というわけで,Stanを使ったM-1記事,他にもお待ちしてますー!