この記事は、Stanアドベントカレンダー2020の16日目の記事、およびベイズ塾アドベントカレンダー2020の16日目の記事です。
今回はちょっと心理統計的なネタです。でも調査票を使うすべての人にとって有用な方法だと思うのでご紹介。
リッカート尺度による心理測定
心理尺度でリッカート法と呼ばれるタイプの尺度構成法があります。

上はローゼンバーグの自尊感情尺度(以下、自尊心尺度)ですが、文章について当てはまる、当てはまらないという数段階の反応ラベルについて回答を求めるタイプのものです。上の例は5件法のリッカート尺度といいます。
リッカート尺度は作るのが簡単というメリットがある一方、測定上いろいろ問題があることがわかっています。たとえば、日本人は「どちらともいえない」という反応ラベルに回答しやすい、中点反応スタイルを持っていると言われます。白黒つけたくない文化的な影響があるのかもしれません。また、「全く当てはまらない」や「非常に当てはまる」など、極端な反応ラベルに回答しやすい人もいます。
基本的には、リッカート尺度への反応は、その人のパーソナリティ(上の尺度なら自尊心)や態度といった心の特性に応じて反応すると考えられていますが、そういった文化や個人によって異なる「反応スタイル」の影響が混在している可能性があります。
最新の項目反応理論では、これらの影響を除去しつつ、潜在変数を推定する方法がいろいろ提案されています。
反応スタイルを潜在変数と区別して推定する方法
反応スタイルは、上でも書いたように、極値(5件法なら1と5)に反応しやすい極値反応スタイル(ERS)、中点(5件法なら3番め)に反応しやすい中点反応スタイル(MRS)、そして肯定的な反応(4と5)に偏る黙従傾向スタイル(ARS)などがあります。たぶんほかにもあります。
反応スタイルを除去する方法として、アンカリングヴィネット法があります。これについては、北條さんのこちらの論文がわかりやすいので詳しい説明は割愛しますが、ざっくりいえばヴィネット法を応用して、人々の反応傾向を補正しようとする方法です。
この方法を使えば、たとえば日米での準拠集団効果の除去などができる可能性があります。ただ、パーソナリティだとやりやすいですが、態度だと他者がこのように思っていると思ってる、みたいなメタ認知が入り込んできて測定がややこしくなります。
もう一つの方法は、Falk, & Cai (2016)の名義IRTを用いた完全情報アプローチがあります。これは、たとえば5件法尺度の場合、順序性を仮定した多値IRT(あとで紹介する一般化部分採点モデルなど)では説明できない部分を反応スタイルとみなす、というアプローチです。名義IRTに比べて順序性を仮定した多値IRTは制約が強いのですが、その制約を部分的に外してやることで、反応スタイルを推定します。
完全情報アプローチによる確率モデル
まず、一般化部分採点モデル(GPCM)から説明します。GPCMは反応ラベルに順序性を仮定したIRTで、確率モデルは次のようなものです。反応ラベル数Kは今回は5件法を考えるので5です。
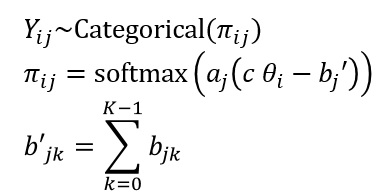
確率変数Yは回答者iが項目jに、反応ラベルk {0, 1, ..., K-1}に反応した結果で、カテゴリカル分布に従うと仮定します。そしてK次元ベクトルの確率πがパラメータです。さらに、aは識別力、bは閾値、θは潜在変数(今回なら自尊心)を表します。cは(0,1,...,K-1)のK次元ベクトルです。
※今回はGPCMでもちょっと特殊な表記を使っていますが、あとの話に繋げやすくするためです。なぜこんなモデルになるのかについては、GPCMの提案者である村木先生の本、「シリーズ行動計量の科学 項目反応理論」を見てください。
さて、Falkらのモデルは、これに反応スタイルを加えていきます。softmax内部の式は、それぞれの反応ラベルへの回答のしやすさを表していると考えればよいです。そして、このGPCMでは捉えられない反応確率を反応スタイルの影響であると考えるわけです。
そこで、各ラベルへの反応のしやすさをK次元ベクトルηで表したとすると、ηはGPCMの反応のしやすさに加えて、ERS、MRS、ARSの反応スタイルを次のように足し合わせます。
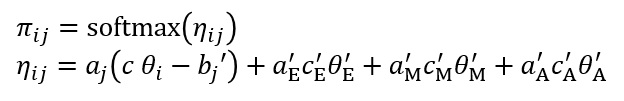
ここで、c'_Eは(1,0,0,0,1)のベクトル、c'_Mは(0,0,1,0,0)のベクトル、c'_Aは(0,0,0,1,1)のベクトルです。a'はそれぞれの反応スタイルの重みで、θ'は反応スタイルの個人差です。
このように、名義IRTの自由度から考えると、ここまでIRTの情報を増やすことができます。元の論文では、識別力aについても反応ラベルごとに別に推定するモデルが提案されていますが、今回は簡単にするために各項目で1つに固定します。
ただ、黙従傾向ARSを推定するときには、項目内に逆転項目が含まれている方がいいでしょう。というのは、もし逆転項目が入っていない場合、肯定反応がしやすいのは、自尊心が高いからなのかどうかと区別しにくくなるからです。逆転項目があっても「当てはまる」に答えやすい人は、ARSの人である、といえるからです。その代わり、逆転項目ではθにマイナスを付けます。
実データを使ってStanコードで推定
今回は、自尊心尺度を300人程度に測定した実データを使って、上のモデルで反応スタイルを除去した潜在変数を推定してみます。
反応傾向を推定するIRTのStanコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
data { int<lower=1> N; // number of data point int<lower=1> P; int<lower=1> S; int<lower=1> G; vector[S] c_d[G]; vector[P] Rev; int Y[N,P]; // observations } transformed data{ vector[S] c = cumulative_sum(rep_vector(1,S))-1; } parameters{ vector[N] theta; real<lower=0> a[P]; vector[S-1] b[P]; vector[N] theta_d[G]; real<lower=0> a_d[G]; } model { //model for(n in 1:N){ for(p in 1:P){ vector[S] eta; vector[S] thr = cumulative_sum(append_row(0,b[p])); if(Rev[p]==0){ eta = a[p]*(c*theta[n]-thr); }else{ eta = a[p]*(c*-theta[n]-thr); } for(g in 1:G){ eta += a_d[g]*c_d[g]*theta_d[g][n]; } Y[n,p] ~ categorical_logit(eta); } } //prior theta ~ normal(0,1); a ~ student_t(4,0,2.5); for(p in 1:P) b[p] ~ student_t(4,0,2.5); for(g in 1:G) theta_d[g] ~ normal(0,1); a_d ~ student_t(4,0,2.5); } |
基本的には上に書いたモデルをそのままStanコードにしただけですが、簡単に解説を。
Revは逆転項目を0,1で指定しています。1なら逆転項目です。ベクトルcでは(0,1,2,3,4)というベクトルを作っています。thrは上のモデルでのb'です。categorical_logitはsoftmaxを入れる前のηをダイレクトに入れることができます。
これを以下のRコードで走らせます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
library(rstan) dat <- read.csv("self_esteem.csv") N <- nrow(dat) P <- 10 S <- 5 G <- 3 Rev <- c(0,0,1,0,1,0,0,1,1,1) ERS <- c(1,0,0,0,1) MRS <- c(0,0,1,0,0) ARS <- c(0,0,0,1,1) c_d <- array(dim=c(G,S)) c_d[1,] <- scale(ERS) c_d[2,] <- scale(MRS) c_d[3,] <- scale(ARS) datastan <- list(N=N,P=P,S=S,G=G,c_d=c_d,Rev=Rev,Y=dat[1:10]) model <- stan_model("response_style.stan") fit <- sampling(model,data=datastan,chains=2,cores=2) |
ERSなどをscale()してるのは、あとでa'をみてどのスタイルの重みが大きいのか比較しやすくするためです。
結果を見てみましょう。識別力と閾値を出力します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
> print(fit,pars=c("a","b")) Inference for Stan model: response_style. 2 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat a[1] 1.84 0.01 0.25 1.40 1.67 1.83 2.00 2.38 898 1 a[2] 1.48 0.01 0.21 1.12 1.34 1.47 1.61 1.91 957 1 a[3] 0.83 0.00 0.12 0.60 0.75 0.83 0.91 1.08 960 1 a[4] 0.81 0.00 0.12 0.60 0.73 0.80 0.88 1.06 1306 1 a[5] 1.13 0.00 0.15 0.86 1.03 1.13 1.23 1.45 1313 1 a[6] 1.37 0.01 0.18 1.03 1.25 1.36 1.48 1.73 1257 1 a[7] 1.28 0.01 0.17 0.98 1.17 1.27 1.39 1.62 1094 1 a[8] 0.32 0.00 0.07 0.20 0.27 0.31 0.36 0.47 1260 1 a[9] 1.16 0.01 0.17 0.88 1.04 1.15 1.28 1.52 791 1 a[10] 1.66 0.01 0.23 1.22 1.50 1.65 1.81 2.16 900 1 b[1,1] -3.51 0.01 0.45 -4.51 -3.79 -3.47 -3.19 -2.74 1369 1 b[1,2] -1.04 0.00 0.14 -1.33 -1.14 -1.04 -0.94 -0.77 1211 1 b[1,3] -0.68 0.00 0.14 -0.97 -0.76 -0.68 -0.59 -0.42 1037 1 b[1,4] 1.90 0.01 0.21 1.51 1.75 1.89 2.04 2.35 951 1 b[2,1] -2.74 0.01 0.33 -3.47 -2.96 -2.72 -2.50 -2.15 1383 1 b[2,2] -1.05 0.00 0.16 -1.38 -1.16 -1.05 -0.95 -0.74 1391 1 b[2,3] -0.42 0.00 0.14 -0.71 -0.52 -0.42 -0.32 -0.16 1048 1 b[2,4] 2.19 0.01 0.26 1.72 2.00 2.17 2.35 2.74 1069 1 b[3,1] -3.15 0.02 0.49 -4.27 -3.44 -3.10 -2.81 -2.33 990 1 b[3,2] 0.34 0.01 0.25 -0.13 0.17 0.33 0.51 0.86 1468 1 b[3,3] -0.55 0.01 0.26 -1.08 -0.71 -0.54 -0.37 -0.06 1138 1 b[3,4] 3.09 0.01 0.45 2.34 2.77 3.06 3.37 4.13 1045 1 b[4,1] -4.69 0.02 0.74 -6.34 -5.12 -4.61 -4.16 -3.44 1327 1 b[4,2] -0.54 0.01 0.27 -1.08 -0.72 -0.55 -0.37 0.02 2341 1 b[4,3] -1.42 0.01 0.30 -2.06 -1.61 -1.40 -1.21 -0.91 1264 1 b[4,4] 3.43 0.01 0.50 2.53 3.07 3.39 3.73 4.52 1291 1 b[5,1] -2.84 0.01 0.36 -3.62 -3.07 -2.82 -2.59 -2.21 1198 1 b[5,2] -0.23 0.00 0.18 -0.56 -0.35 -0.22 -0.11 0.11 1646 1 b[5,3] -0.28 0.00 0.17 -0.65 -0.39 -0.28 -0.16 0.03 1637 1 b[5,4] 2.10 0.01 0.29 1.59 1.91 2.09 2.29 2.73 1257 1 b[6,1] -2.27 0.01 0.26 -2.83 -2.44 -2.25 -2.09 -1.80 1083 1 b[6,2] -0.22 0.00 0.15 -0.50 -0.32 -0.22 -0.13 0.08 1412 1 b[6,3] -0.01 0.00 0.15 -0.32 -0.11 -0.01 0.09 0.28 1582 1 b[6,4] 1.85 0.01 0.24 1.43 1.68 1.83 1.98 2.35 1055 1 b[7,1] -2.24 0.01 0.27 -2.81 -2.42 -2.22 -2.04 -1.75 1084 1 b[7,2] 0.00 0.00 0.15 -0.28 -0.10 0.00 0.09 0.32 1472 1 b[7,3] 0.02 0.00 0.16 -0.29 -0.09 0.03 0.13 0.30 1308 1 b[7,4] 2.54 0.01 0.31 2.00 2.32 2.53 2.74 3.21 1063 1 b[8,1] -6.28 0.04 1.89 -10.62 -7.34 -6.05 -4.99 -3.18 2436 1 b[8,2] -0.77 0.02 0.86 -2.42 -1.34 -0.78 -0.19 0.89 3177 1 b[8,3] -5.48 0.04 1.34 -8.81 -6.19 -5.32 -4.51 -3.44 1329 1 b[8,4] 0.09 0.01 0.53 -1.00 -0.24 0.08 0.44 1.10 2008 1 b[9,1] -2.43 0.01 0.32 -3.09 -2.64 -2.41 -2.21 -1.87 1063 1 b[9,2] 0.24 0.01 0.21 -0.15 0.10 0.23 0.38 0.70 1319 1 b[9,3] -0.86 0.01 0.24 -1.35 -1.01 -0.84 -0.69 -0.45 1090 1 b[9,4] 1.66 0.01 0.24 1.23 1.50 1.64 1.81 2.20 1023 1 b[10,1] -1.74 0.01 0.21 -2.19 -1.87 -1.73 -1.60 -1.37 952 1 b[10,2] 0.04 0.00 0.13 -0.20 -0.04 0.03 0.12 0.30 1363 1 b[10,3] 0.56 0.00 0.14 0.28 0.46 0.55 0.65 0.83 999 1 b[10,4] 1.80 0.01 0.21 1.42 1.65 1.78 1.93 2.25 1313 1 |
きれいに収束しています。
反応スタイルの重みを見てみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> print(fit,pars=c("a_d")) Inference for Stan model: response_style. 2 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat a_d[1] 0.74 0 0.06 0.62 0.70 0.74 0.78 0.88 856 1 a_d[2] 0.29 0 0.04 0.21 0.27 0.30 0.32 0.37 630 1 a_d[3] 0.28 0 0.06 0.16 0.24 0.28 0.31 0.38 437 1 Samples were drawn using NUTS(diag_e) at Tue Dec 15 21:44:39 2020. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). |
極値バイアスの重みが大きいことがわかります。
続いて、尺度得点と反応スタイルを除去した潜在得点の関連です。
|
1 2 3 4 |
library(magrittr) theta <- rstan::extract(fit)$theta %>% apply(2,mean) SE <- (dat$SE1 + dat$SE2 + (6-dat$SE3) + dat$SE4+ (6-dat$SE5) + dat$SE6 + dat$SE7 + (6-dat$SE8) + (6-dat$SE9) + (6-dat$SE10))/10 plot(SE,theta) |
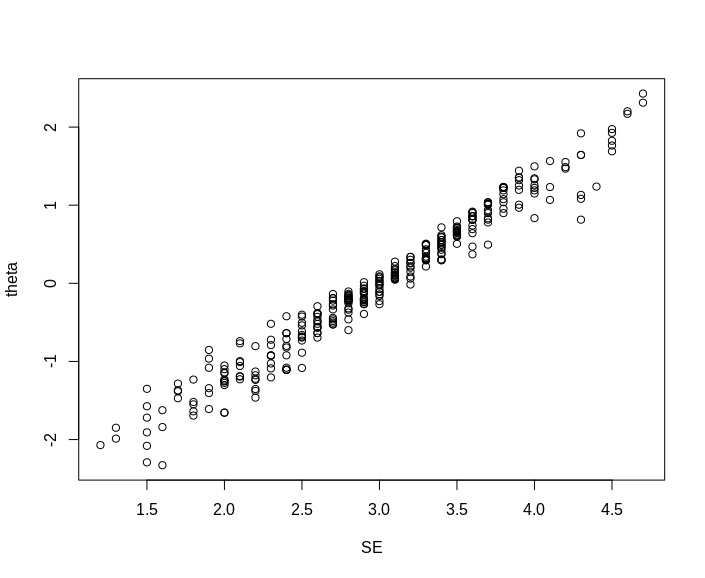
かなり高い相関がありますね。相関は0.98とかなり高いです。今回のデータだと、あまり反応スタイルの影響がないのかもしれません。ただ、一部の人で尺度得点は高いが、thetaはちょっと下がっている人がいます。
まとめ
今回は、自尊心尺度だけで反応スタイルの推定を行いましたが、他の同じ5件法の尺度を使って、それらで反応スタイルが共通しているという仮定のもとで推定することもできると思います。
また、アンカリングヴィネット法は準拠集団効果も除去できますが、今回の記事で紹介した完全情報アプローチでは、準拠集団効果の除去は難しいです。逆に、両方の方法をドッキングさせれば、もっと安定した方法になるかもしれません。
あまり時間がなかったので簡単な紹介になりましたが、追加のデータがいらない方法ではあるので、一度使ってみてはどうでしょう。