ひさびさの記事です。
ほぼアドカレ専用ブログと化してます。
この記事はJASP Advent Calendar 2021の9日目の記事です。
JASPって何?という人は小杉先生のこちらの記事を御覧ください。
簡単に言えば、GUIの統計ソフトで、Rより使いやすく、SPSSより軽い、そしてなにより無償であること、が特徴です。
開発はオランダのWagenmakersらのチームが行っています。心理統計の専門家なので分析結果についてはかなり安心できるのではないかと思います。
バージョン16から日本語化されたことで、翻訳をしているベイズ塾メンバーたちがこれから注目を集めさせようとしているいまとても注目を集めている統計ソフトです。
※なお、私もこの記事を書いてることで、まるで翻訳もしたかのような顔をしてますが、私はぜんぜん携わってません。ベイズ塾のメンバーを中心とした素晴らしい方々の努力の賜物です。
この記事では、JASPの軽い紹介と、JASPで計算されるベイズファクターってどんなのかな?というような話をしていきたいと思います。
◆JASPの特徴
JASPは上にも書いたように無償のGUI統計ソフトウェアです。最近そういうの増えてますね。jamoviとか。あとなんだっけ、ほら、日本で有名なあのソフト。とか、いろいろあります。
そのなかでJASPの特徴を最も象徴しているのはベイズ統計による分析でしょう。Wagenmakersはベイズ統計推しの統計学者なこともあって、ベイズ統計による基本的な分析ができるようになっているのです。
たとえば、平均値の差の推定、相関係数の推定、分散分析、回帰分析などなど。これらがすべてベイズ統計の枠組みで推定できます。こりゃすごい。
ベイズ統計による分析、といってもいろいろありますが、JASPではこれらの基本的な統計分析にベイズファクターという指標を出してくれます。ベイズファクターについて語ると長くなるので詳しくは以下の岡田謙介さんの論文とかをどうぞ。
ざっくりいえば、「効果がない」という仮説と、「効果がある」という仮説について、どちらが支持されているといえるかを表す指標です。帰無仮説検定と違って、効果がないことを積極的に支持することができるという点が特徴といえるでしょう。
よく言われる基準として(これはあくまで「よく言われる基準」にすぎません)、ベイズファクターが3以上、あるいは10以上あれば「効果がある」仮説を支持している、というものがあります。
それでは、さっそくJASPを使って平均値の差の推論についてベイズファクターを計算してみましょう。データはRで適当に生成します。
|
1 2 3 4 5 6 7 8 9 10 11 |
## data N <- 25 mu1 <- 5 mu2 <- 3 sigma <- 2 set.seed(12345) X1 <- rnorm(N,mu1,sigma) X2 <- rnorm(N,mu2,sigma) data <- data.frame(X=c(X1,X2),con=c(rep(1,N),rep(2,N))) write.csv(data,"data.csv") |
上のコードのように、平均値に2の違いがある正規分布からそれぞれ生成しました。サンプルサイズは25です。
いまdata.csvというファイルを作ったのでこれを適当なフォルダに移動させるかして、JASPで読み込めるようにしましょう。
R上でとりあえずt検定をやってみましょう。
|
1 2 3 4 5 6 7 8 9 10 |
Welch Two Sample t-test data: X1 and X2 t = 2.4992, df = 46.044, p-value = 0.01608 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0.3529542 3.2746734 sample estimates: mean of x mean of y 4.912289 3.098475 |
有意でした。
◆JASPを使おう!
まずはJASPを起動します。
とりあえず、左上の三本線のところをクリックします。困ったらここをクリックです。それで大抵解決します。
そして一番上の「開く」→「コンピュータ」を選んでいくと、「参照」ボタンがありますのでそれをクリックします。あとはご自身のパソコン内のデータファイルを選びましょう。
ファイル形式はcsvファイルがオススメです。上で保存したdata.csvを選択してみましょう。
ちゃんと読み込めてるのがわかります。
さて、ではベイジアンt検定をやってみましょう。
上のメニューに有る「t検定」を選ぶと、「伝統的」と「ベイジアン」の2つが出てきます。伝統的は、いわゆる頻度主義統計に基づくもの、ベイジアンはベイズ統計に基づくものです。ベイジアンを選び、独立したサンプルのt検定を選択しましょう。
従属変数はX、グループ化変数はconですので、それぞれ指定します。
対立仮説は、ここではグループ1≠グループ2を選んでおきます(基本使われるのはこれ)。あと、「事前分布と事後分布」もチェックしておくとビジュアルが楽しいです。
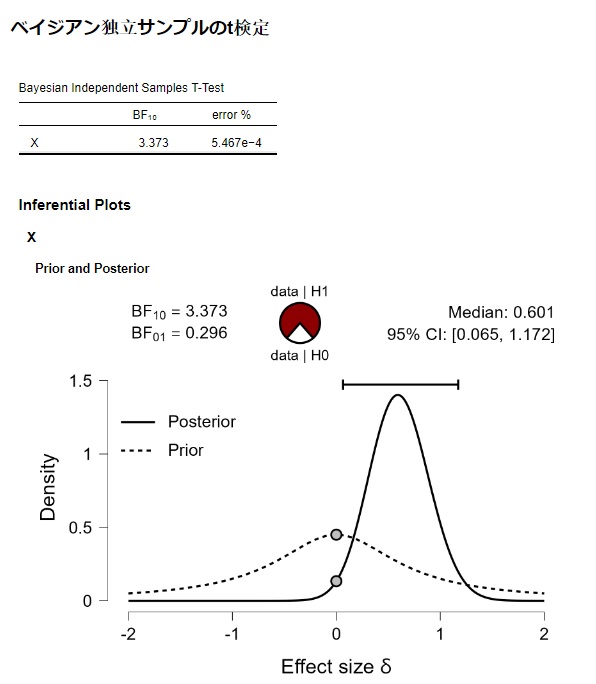
さて、ベイズファクターは3.373と計算されました。
検定結果も有意でしたが、ベイズファクターでも「効果がある」ほうが支持されたという結果が得られました。
お手軽ですね。
JASPはベイズファクターは解析的に解いています。なので計算が一瞬なんですね。
でもお手軽すぎて、「中身どうなってんの」って気になりますよね。
というわけでStanを使ってMCMCで同じことを再現してみましょう。
◆Stanを使って平均値の差についてのベイズファクターを計算する
さて、JASPについての記事なのに無理やりStanをねじ込んでくるあたり、Stan中毒者っぽいですね。
StanなどのソフトでMCMCによってベイズファクターを計算するためには、bridesamplingという方法で周辺尤度を推定することで行います。それはbridesamplingパッケージを使えば簡単です。
ベイズファクターの計算のためには、対立仮説(差がある)の周辺尤度と、帰無仮説の周辺尤度をそれぞれ計算し、その比を求めます。
というわけで、対立仮説と帰無仮説それぞれのStanコードを書きます。
ただ注意点があって、読み込むデータは標準化しておく必要があります。これは、統計モデルの事前分布がデータのスケールに依存してしまうため、それを整えておくための手続きです。
※このあたりの妥当性(スケーリングと事前分布の関係)についてはいろいろ議論がありえますが、この記事ではあまりつっこみません
まずはStanコードを紹介し、そのあとRコードを紹介します。
Stanコード(対立仮説)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
data{ int N; real X1[N]; real X2[N]; real delta_prior; real mu_prior; real sigma_prior; } parameters{ real delta; real mu; real } model{ real a = delta*sigma; target += normal_lpdf(X1 | mu + a/2, sigma); target += normal_lpdf(X2 | mu - a/2, sigma); target += cauchy_lpdf(delta | 0, delta_prior); target += cauchy_lpdf(mu | 0, mu_prior); target += cauchy_lpdf(sigma | 0, sigma_prior)-log(0.5); } |
Stanコード(帰無仮説)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
data{ int N; real X1[N]; real X2[N]; real delta_prior; real mu_prior; real sigma_prior; } parameters{ //real delta; real mu; real } model{ //real a = delta*sigma; target += normal_lpdf(X1 | mu , sigma); target += normal_lpdf(X2 | mu , sigma); //target += cauchy_lpdf(delta | 0, delta_prior); target += cauchy_lpdf(mu | 0, mu_prior); target += cauchy_lpdf(sigma | 0, sigma_prior)-log(0.5); } |
Stanコードについてのポイントは以下です。
- bridge samplingを使うためにはStanコードはターゲット記法で書かないといけない。
- 確率モデルは「ベイズ統計で実践モデリング」のp110に書いてます。
- 標準化差(デルタ)、平均値、標準偏差はすべてコーシー分布を事前分布にする。標準偏差は半コーシー分布なので-log(0.5)をつけておく。
- 事前分布のハイパーパラメータ(コーシー分布の尺度パラメータ)は、標準化差(デルタ)については0.707(JASPのデフォルト)、ほかは1にしておく。
Rコードは以下です。今回はこだわりを捨ててrstanでやりました(謎
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
library(cmdstanr) library(bridgesampling) library(rstan) ## model rstan.test <- stan_model("bayes_test.stan") rstan.null <- stan_model("bayes_null.stan") ## scaling temp <- scale(c(X1,X2)) X1 <- temp[1:25,] X2 <- temp[26:50,] ## prior delta_prior <- 0.707 mu_prior <- 1 sigma_prior <- 1 ## data for stan datastan <- list(N=N, X1=X1, X2=X2, delta_prior=delta_prior, mu_prior=mu_prior, sigma_prior=sigma_prior) ## MCMC test fit.test <- sampling(rstan.test, datastan, iter = 11000, warmup = 1000, chains = 4, cores = 4) fit.null <- sampling(rstan.null, datastan, iter = 11000, warmup = 1000, chains = 4, cores = 4) ## bridge sampling bs.test <- bridge_sampler(fit.test,method="warp3") bs.null <- bridge_sampler(fit.null,method="warp3") ## bayes factor bayes_factor(bs.test,bs.null) |
ポイントとしては、以下の点があります。
- データは標準化しておく。
- bridge samplingを使うためにはMCMCのサンプルサイズは十分大きな数が必要(今回は4万回)。
走らせた結果、ベイズファクターは3.376となりました。
![]()
JASPの結果(3.373)とほぼほぼ一致してますね!
◆まとめ
このように、JASPのベイズファクターの計算をMCMCで再現できました。
ベイズファクターは標準化差デルタの事前分布のハイパーパラメータによって結構変わります。JASPでは、ベイズファクターについての感度分析を簡単に実行できるのもすばらしい点です。
ベイズファクターの頑健性チェックをチェックすると、
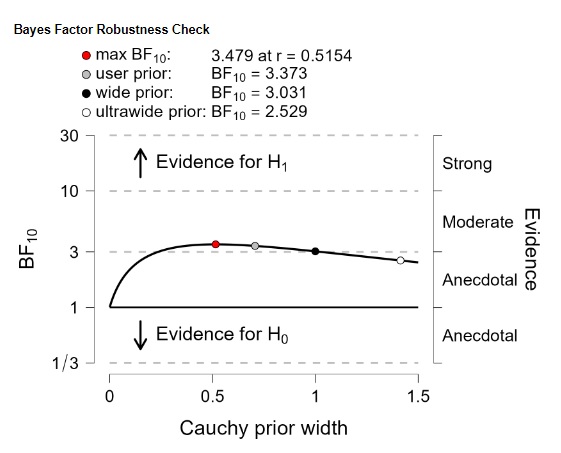
事前分布のパラメータによってベイズファクターがどう変わるかを確認できます。見たところ、0.2~1ぐらいの範囲で3を超えているのが確認できます。なので、今回のデータについては通常考えられる範囲についてはほぼほぼ大丈夫、という感じではないでしょうか。
ついでに、StanでMCMCするバージョンで、事前分布のパラメータを1にしたとき、ベイズファクターは3.0329となり、これもやはりJASPの結果(上のWide priorに対応)と一致しました。
この記事でわかったこととして、JASPのベイズファクター計算のポイントは、
- まずデータを標準化する
- 差があるというモデルと、差が0に固定したモデルの周辺尤度を計算し、その比で計算される
- 事前分布は、尺度パラメータを決める必要がある。標準化差については0.707(ただし、これはデフォルトであって要感度分析)、それ以外は1を尺度パラメータにしたコーシー分布にする。
ということです。