潜在ランク分析のRコードを作りました

先日，HAD13.02に搭載された，連続変量に対する潜在ランク分析のコードをRに翻訳してみました。

コードはこちらです。

このコードでは，複数の連続変量を与えることで，参加者を潜在的な順序グループに分類する分析を行います。なお，潜在ランク分析そのものについてはこちらの記事を参照してください。

推定は，生成位相マップ(Generative Topographic Mapping: GTM)を用いて推定しています。簡単に言うと，混合分布モデルに順序の制約を与えたものです。いまのところ，連続変量のみが対応しています。順序尺度版も気が向いたらやりますが，今のところ難しいと思います（HADでは実装されています）。

なお，この潜在ランク分析とこの関数については，2月14日に比治山大学で行われるHiroshimaR#3で発表予定です。興味ある方はぜひお越しください。

◆分析例

それでは2014年のプロ野球選手，打者99名（年俸上位100名から0打席の一人を除外）を対象を分析したものを例に，関数の使いかたについて簡単に説明します。

なお，上記のサンプルデータはここにあります。

まず，データをdatに読み込みます。

dat <- read.csv("baseball.csv")

データには，打率，安打数，本塁打数，打点の4つを入れてます。

head(dat)

次に，潜在ランク分析を実行するための関数を読み込みます。

source("latent_rank.r")

潜在ランク分析は，LRA（）という関数で実行します。引数は，データセット，ランク数だけを入力すればOKです。今回は，5ランクで推定してみましょう。結果はsummary関数にいれます。

result <- LRA(dat, 5)
summary(result)

すると，上のように各ランクの潜在度数，ランクごとの各変数の平均値，潜在ランクと変数の順位相関係数が出力されます。

潜在度数は，潜在確率にサンプルサイズをかけたもので，各ランクに何人いるかを表しています。今回の例ではそこそこ散らばっているようです。

平均値を見ると，ランク1は打率が2割1分，9安打，0.4本塁打，4.7打点と，へぼへぼ選手であることがわかります。ランク3ぐらいになるとそこそこに，ランク5になるとかなりの成績になってきます。

潜在ランクとの順位相関は，各変数がどれほどランクの推定に貢献しているかがわかります。今回のランクは打点と高い相関があるようです。

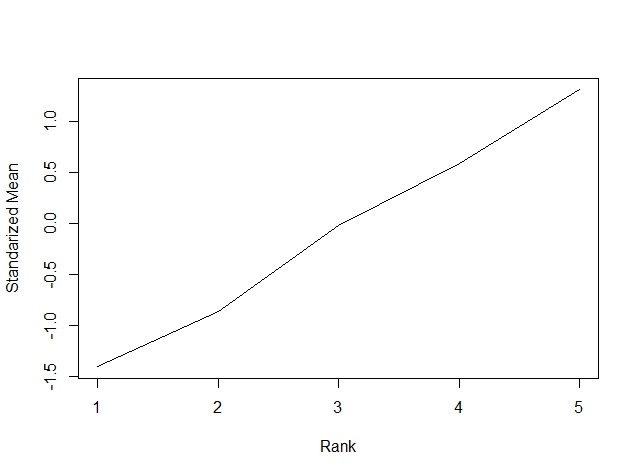
続いて，plot関数に結果を入れると，次のようなグラフが出力されます。

plot(result)

 このグラフは，ランクによる主成分得点の推定値です。この主成分得点が小さいランクほど小さい値になることが，ランクの順序配置の条件としています。

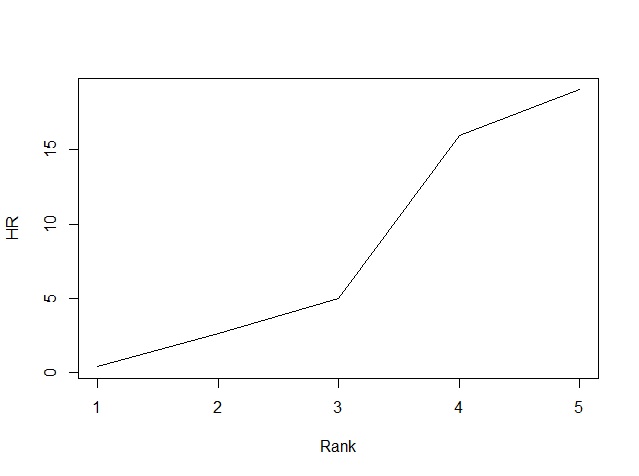
次に以下のように変数の番号を入れると，変数ごとのプロットを見れます。3番めの本塁打のプロットを見てみましょう。

plot(result,3)

 ややガタついていますが，順序性は保持されています。なお，各変数については順序配置が満たされないこともあります。

情報量規準を見る場合は，AIC関数に入れます。

AIC(result)

情報量規準を見ることで，何ランクが適切であるかが推定できます。実は，このデータの場合，5ランクがAIC最小になります。

なお，各参加者のランクを知りたい場合は，

rank5 <- result$rank
rank5

また，各参加者の潜在ランクへの所属確率（負担率）を知りたい場合は，

syozoku <- result$res

で知ることができます。

その他オブジェクトは，対数尤度が"ll"，分散が"vars"，混合確率が"prob"，収束回数が"count"，などです。