HAD13から,混合分布モデルや潜在クラス分析が実行できるようになりました。
これらを総称して,潜在変数モデル,あるいは潜在構造分析と呼んだりします。変数を使って,潜在的な母集団を見つけ出す分析手法です。
混合分布モデルは,クラスタ分析に似た方法で,調査回答者を変数に基づいてグループ分けをする,という点では同じです。ただ,クラスタ分析が変数の「距離」に基づいて回答者を分類しているのに対して,混合分布モデルは確率分布を仮定することで,尤度を用いて回答者を分類します。
尤度を使ってクラスタを推定するメリットは,データに最も合ったモデルを選択することができる,という点にあると思います。クラスタ分析などはデンドログラムなどを使って視覚的にクラスタ数を判断しますが,混合分布モデルでは,AICなどの情報量規準を使ってクラスタ数を判断することができるのです。
もう一つのメリットは,各回答者がどのクラスタに所属するかを,確率的に推定することができる,という点にあります。階層クラスタやk-means法などは回答者を無理やりクラスタにわけますが,混合分布モデルでは,回答者はグラデーション的にクラスタに所属することになります。それによって,より細やかな推定が可能になっているわけです。
データを使って混合分布モデル
データを使って,実際に混合分布モデルを実行してみましょう。
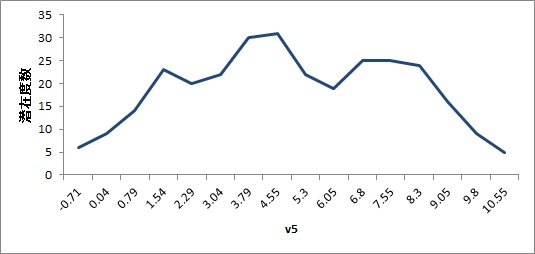
例えば,以下の様なヒストグラムのデータがあったとします。これは実は3つのグループから正規乱数を発生させたものを合成したデータです。なんとなく,3つ山があるのがわかると思います。
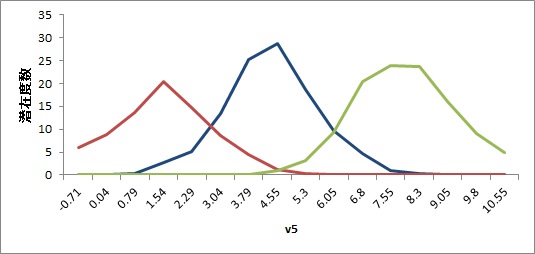
このデータに対して,混合分布モデルを適用してみます。データ発生メカニズムどおり,3つの潜在クラスタを仮定します。すると,潜在度数分布は以下のようになります。
このように,比較的綺麗に3つの正規分布のデータが抽出できているのがわかると思います。なお,潜在クラスタが2つの場合,4つの場合と比較しても,AICは3が最も小さいという結果が得られました。このように,尤度を用いて推定しているので,情報量規準も利用できるのがメリットです。
一方,このデータに階層クラスタ分析(ウォード法)を適用すると,以下の様なデンドログラムになります。見てわかるように,2つのクラスタが抽出されているのがわかります。もともとデータの発生メカニズムは3つの正規母集団なので,階層クラスタはうまくそれを推定できていない事がわかります。
混合分布モデルは,もちろん他のクラスタ分析と同様に,複数の変数を使って回答者を分類することができます。例えば,2014年の野球選手100人の成績を使って,混合分布モデルを適用してみましょう。
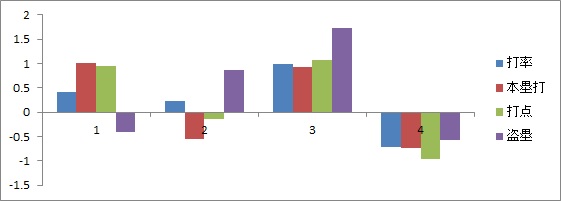
入力したデータは,打率,本塁打数,打点,盗塁の4変数です。すると,以下の様なパターンのクラスタが得られました。情報量規準から,4クラスタが選択されました。
これを見ると,1番目は本塁打と打点が高いグループ,2番めは,本塁打が少なくて盗塁が多いグループ,3番めはすべてが高いグループ,4番目はすべてが低いグループに別れることがわかります。一流の選手はなんでもやってのける,ということでしょうか。
混合分布モデルの設定
混合分布モデルは,このように複数の変数を使って,データをクラスタに分ける分析手法です。混合モデルには,実はいろいろなモデルを選択することができます。
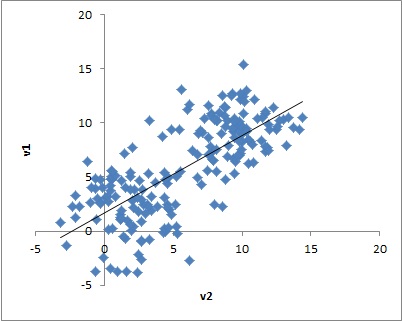
まず,クラスタに分けたあとの変数間の相関を仮定するかしないか,という設定です。たとえば,次のような散布図が描けるデータがあったとします。
一見して,相関がある二変数のようですが,よく見ると,二つの変数が無相関になる二つのグループが混ざっています。このように,混合分布モデルでは,データ間の相関がなくなるようなグループを見つける,という側面もあるわけです。なので,データ間の相関がない,という仮定で推定することが多いように思います(もちろん場合による)。
ただし,データ間の相関がないグループを探索するためには,かなりの数のクラスタにわけないといけない,ということもあります。情報量規準がいつまでたっても減っていくので,クラスタ数が10数個になってしまう,ということもあります。少数のグループを見つけたい場合は,いっそ変数間の相関を仮定した推定をしてみるのもいいでしょう。すると,比較的少ないクラスタ数で情報量規準が最小になると思います。
なお,相関がないという仮定で推定する混合分布モデルを,潜在プロフィールモデル,と呼ぶことがあります。潜在プロフィールモデルは,混合分布モデルの特殊なバージョンだといえるでしょう。
次に,各クラスタ間の相関関係が等しいかそうでないか,という設定も可能です。上の散布図を見ると,データの分散はだいたい同じような感じに見えます。しかし,例えばデータから異端な集団を取り出したい,という場合には,分散が等しいという仮定は無理があります。
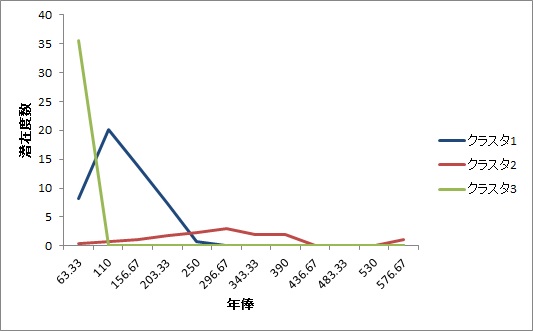
例えば野球選手の年俸を3つのクラスタに分けた例です。
野球選手の年俸にはかなりの分布が歪んでおり,極端に少ない選手,平均的な選手,そして高給取りの選手,という3つに分けたときに,分散が等しいという仮定はかなり無理があるでしょう。このデータで分散が等しいと仮定すると,情報量規準は大幅に上がってしまい,また潜在度数が一人だけが所属するクラスタ,という解釈のしにくい結果が得られてしまいます。
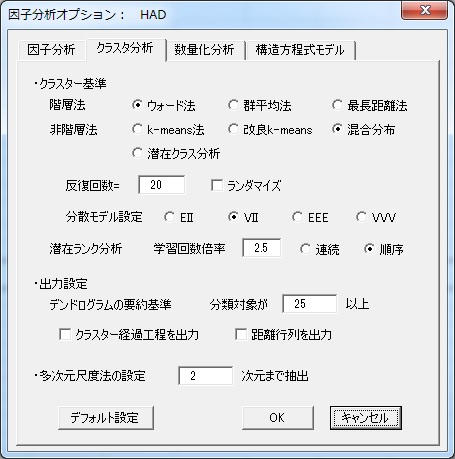
HADでは,4つのモデルを設定できます。EIIとあるのが共分散(相関)を仮定せず,またクラスタ間で分散が等しいという仮定のモデルです。一番シンプルなモデルです。次に,VIIは,分散だけを推定しますが,クラスタ間で異なるという仮定のモデルです。これがデフォルト設定になっています。
続いて,EEEとあるのが共分散も推定するけどクラスタ間でそれが等しいという仮定のモデルです。最後にVVVが共分散を推定し,さらにクラスタ間で異なるという一番複雑なモデルです。
モデルが複雑になるほど,情報量規準の提案するクラスタ数は少なくなる傾向にあります。とくにBICはシンプルなモデルを好みます。
潜在クラス分析
潜在クラス分析は,混合分布モデルと違って,入力するデータが名義尺度のデータになります。つまり,名義尺度データから潜在的な名義グループを推定する方法です。いわば名義尺度版の因子分析と言える方法です。
潜在クラス分析は,変数間の連関係数が小さくなるように,潜在クラスを推定します。基本的には混合分布モデルと同じような扱い方ができる方法です。違っているのは,データの尺度水準だけです。
よって,情報量規準を推定できる点や,回答者の所属確率を推定できる点なども同じです。
混合分布モデルの注意点
混合分布モデルは,k-means法と同じように,初期値に結果が大きく依存します。よって,混合分布モデルを使う場合は,複数の初期値から推定を初めて,最も尤度が大きなモデルを選択する,という過程をふみます。なので,反復回数が十分でないと,最適なモデルに到達していない可能性があります。
HADでは乱数で初期の所属クラスタを決めて,まずk-means法であたりをつけます。そのあと混合分布モデルを実行します。これをデフォルトでは20回繰り返して,もっとも尤度の高いモデルを最終的な結果として出力します。ただ,モデルが複雑だったり,回答者数が多いと,20回の反復では十分ではないかもしれません。適宜反復数を増やしてみて,結果を比較してみてください。
また,混合分布モデルは回答者の所属確率をEMアルゴリズムという方法で繰り返し推定を行います。これはとても推定に時間のかかる方法です。大規模なデータの場合,HAD(というかExcel)では半端ない時間がかかってしまう場合があります。
その場合は,計算をかなり簡略化した改良k-means法がオススメです。これは所属確率が0か1のみをとると考えた場合の混合分布モデルであると考えてもらえばいいです。尤度を使って推定する点や,情報量規準を利用できる点などは同じです。所属確率を0と1にだけすることで,計算時間を大幅に減らしています。当然尤度は混合分布モデルのほうがよいですが,多くの場合,それほど結果は変わらないので,データの規模が大きい場合はこちらを使ってみてください。
改良k-means法でも時間がかかる場合は,別のソフトウェアを使うか,普通のk-means法を使ってください。
HADで混合分布モデルを実行する方法
HADで混合分布モデルを実行するには,多変量解析のクラスタ分析を選択したあと,「非階層的」を選択します。そのあと,「オプション」ボタンを押して,下のように「混合分布モデル」を選択します。
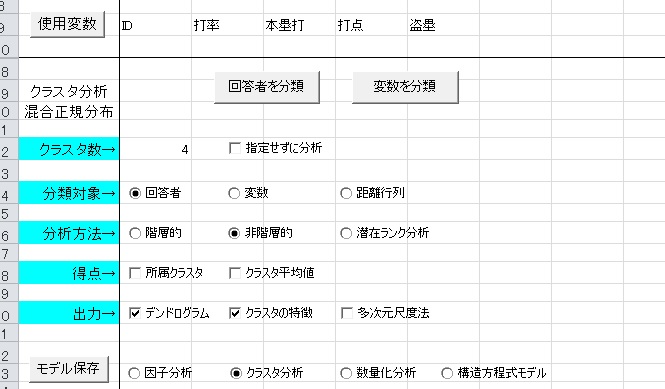
この状態でOKを選ぶと,以下のように「混合分布モデル」と表示されます。
あとは使用変数を指定し,クラスタ数を指定してから実行を押せば,分析結果が出力されます。
分析には大抵時間がかかるので,根気よくお待ちください。