ひさしぶりのブログ記事です。
今回は、項目反応理論をStanで実行するときに知ってると便利なことをまとめておきたいと思います。
項目反応理論とは、テストについての計量モデルで、問題に対する正解・不正解のデータから、問題の特性や、回答者の学力を推定するためのモデルです。心理測定学(Psychometrics)において中心的といえば大袈裟かもしれませんが、それぐらい重要なテーマです。
項目反応理論については、小杉先生の資料が参考になります。そちらをどうぞ。なお、これから項目反応理論をIRT(Item Response Theory)と表記します。
2パラメータのIRT
IRTでは、ある問題に正解する確率をロジスティック曲線を用いてモデリングします。この曲線を項目反応関数といいます。代表的なモデルでは、項目反応関数のパラメータとして識別力と困難度の2つを用いて表現します。識別力は項目反応関数の傾き(aと表記で、困難度は曲線の位置(bと表記)を表します。
式で書くと次のようになります。ある問題jに、回答者iさんが正答する(1と答える)確率は、
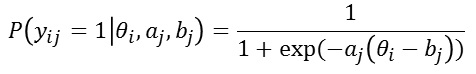
と表現されます。Θはiさんの学力です。
この式に従って、項目反応関数を図で描いてみます。下の図のように、青い線は識別力が高く(a=2)、困難度が中ぐらい(b=0)の項目反応関数、赤い曲線は、識別力が低く(a=0.5)、困難度が高い(b=1)の項目反応関数になっています。
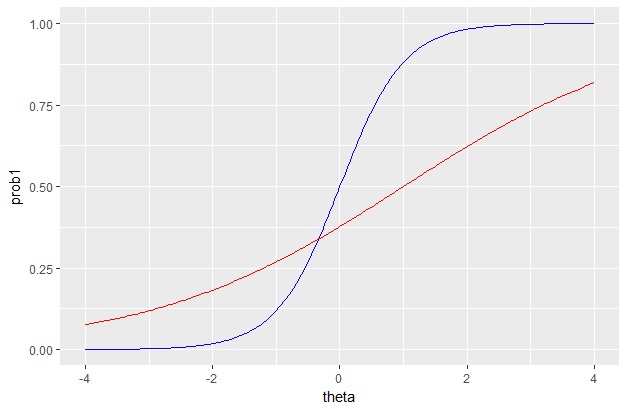
なお、この図は次のコードで描きました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
library(psych) library(ggplot2) a1 <- 2 b1 <- 0 a2 <- 0.5 b2 <- 1 theta <- seq(-4,4,length.out=201) prob1 <- logistic(a1*(theta-b1)) prob2 <- logistic(a2*(theta-b2)) ggdf <- data.frame(theta,prob1,prob2) %>% ggplot ggdf + geom_line(aes(x=theta,y=prob1),color="blue") + geom_line(aes(x=theta,y=prob2),color="red") |
2パラメータIRTをStanで推定
2パラメータのIRTは、確率モデルは次のように書けます。
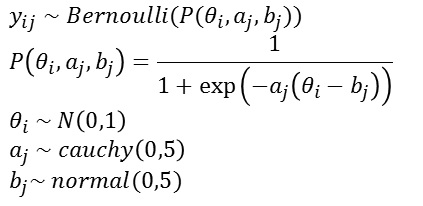
これをStanコードにすると次のような感じになります。Stanにはロジスティック関数を含んだベルヌーイ分布である、bernoulli_logit()という関数があるので、これを使うととても簡単に書けます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
data { int int int y[N,P]; // observations } parameters { real theta[N]; vector vector[P] b; } model { #prior theta ~ normal(0,1); a ~ cauchy(0,5); b ~ normal(0,5); #model for (n in 1:N){ for(p in 1:P){ y[n,p] ~ bernoulli_logit(a[p]*(theta[n]-b[p])); } } } |
IRT用の乱数データを生成させたい
作ったモデルやコードがあってるかを確かめるためには、パラメータを決めてそこから乱数データを作り、モデルで推定した結果が元のパラメータに一致するといいです。
Rには便利な乱数生成用の関数がありますが、ここではStanを使って乱数を生成する方法を紹介します。IRTの場合、2値だと簡単ですが、多値データだとRで乱数作るのが面倒になるので、Stanでやってしまうのがいいかもしれません。
まず、パラメータを決めましょう。識別力と困難度を次のように決めます。
|
1 2 3 4 |
#setting P <- 25 #項目数 a_true <- rep(1.7,P) #因子負荷量初期値 b_true <- seq(3,-3,length.out = P) |
次に、乱数生成用のStanコードを用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
data{ int P; vector[P] a; vector[P] b; } parameters{ real temp; } model{ temp ~ uniform(0,1); } generated quantities{ int y[P]; real theta; theta = normal_rng(0,1); for(p in 1:P){ y[p] = bernoulli_logit_rng(a[p]*(theta-b[p])); } } |
乱数用のコードを作るときに注意が必要なのは、
- parameterブロックとmodelブロックには必須。なので適当なパラメータをいれて、確率モデルを書く必要がある。
- MCMCサンプル1つが1オブザベーションとみなして乱数を作るとやりやすい。たとえばN=1500 と設定したばあい、samplingのオプションでiter=1500,warmup=0,chains=1としておく。
これを走らせるRコードは以下です。
|
1 2 3 4 5 6 7 8 9 |
#data generation model.random <- stan_model("2PL_random_normal.stan") N <- 1500 #サンプルサイズ set.seed(123) data.random=list(P=P,a=a_true,b=b_true) rdata <- sampling(model.random,data=data.random,iter=N,warmup=0,chains=1) dat <- as.data.frame((rstan::extract(rdata)$y)) theta_true <- as.data.frame((rstan::extract(rdata)$theta)) |
モデルが走るか確認する
では、うまく元のパラメータが復元できているか確認してみましょう。
IRTは回帰分析はGLMMなどにくらべて、パラメータ数やデータ数が大きくなりがちです。なので、MCMCでやるとそこそこ時間がかかります。また、多値IRTなどにするとさらに時間が増えるので、まずはモデルがちゃんとうまく走るのかを先に確認することがおすすめです。
まず、パラメータリカバリをするとき、いきなり大きいデータを走らせるのではなくて、小さめのデータを使うといいでしょう。あと、generated quantitiesブロックにエラーがある場合、サンプリングはうまくいくけど、最後の最後でダメー残念ーみたいなときがあります。心が折れるので、最初は200回とか少なめにiterを設定しておくといいでしょう。
実データで走らせるときも、いきなり全部やるのではなくて、一部のデータだけでやってみるのもいいかもしれません。その場合は、次のコードでデータからランダムに一部だけ取り出すことができます。ここでは、500人分のデータだけ取り出す、という例です。
|
1 2 |
sampleID <- sample(N,500) dat2 <- dat[sampleID,] |
大きいデータを推定するとき
ちゃんと走ることが確認できたら、大きいサイズの乱数でモデルをチェックしましょう。ここでは1500人としています。ただ、サンプリングの数を大きくすると時間がかかります。どれくらいのバーンイン(waruup)で収束するかを見極めておくと、あとあと推定が早くすんで便利です。まずはwarmup=200回ぐらいでやってみます。パラメータの分布の性質を知るのに2000ぐらいあればたいていは十分なので、4つのchainを走らせることを考えると、1つのchainでは500あれば十分ということになります。よって、iter=700で走らせてみます。
あと、推定にどれくらい時間がかかるかも知っておくと便利なので、時間計測もやっておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#stan model model.2PL <- stan_model("IRT_2PL.stan") #data for stan N <- nrow(dat) P <- ncol(dat) datastan <- list(N=N,P=P,y=as.matrix(dat)) #sampling t<-proc.time() fit.mcmc <- sampling(model.2PL,data=datastan,iter=700,warmup=200,chains=4,cores=4) proc.time()-t |
ここでの注意は、IRTで渡すデータはint型の配列なので、データフレームではなく、行列形式にして渡しておかないとエラーが出る(なんか最近のバージョンででるようになった)ということです。
あと、とりあえず分析結果を知りたいときには、変分ベイズを使ってみるという手もあります。ただ、変分ベイズは推定は早いですが、あくまで近似的な解である点には注意が必要です。最終的にはMCMCで推定するのがいいでしょう。
|
1 2 3 4 |
#variational Bayes t<-proc.time() fit.vb <- vb(model.2PL,data=datastan,iter=5000,tol_rel_obj=0.0001,eval_elbo=100) proc.time()-t |
vbは初期設定だととても甘い(気がする)ので、tol_rel_objを厳しめにしておきます。0.0001ぐらいにしておくと、MCMCと結構近い点推定値が得られます(これもモデルによります)。IRTは比較的VBでもMCMCに近い解が得られるモデルだと思います。
結果の確認
結果を知るには、print()が一番早いかなーと思います。好みによります。pars=で、見たいパラメータだけを取り出します。
|
1 |
print(fit.mcmc,pars=c("a","b")) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat a[1] 1.30 0.01 0.20 0.91 1.16 1.30 1.43 1.71 1203 1.00 a[2] 1.57 0.01 0.21 1.19 1.43 1.57 1.71 2.01 1299 1.00 a[3] 1.46 0.00 0.17 1.14 1.34 1.46 1.58 1.81 2000 1.00 a[4] 2.13 0.01 0.23 1.69 1.97 2.12 2.27 2.61 2000 1.00 a[5] 1.85 0.00 0.17 1.53 1.73 1.84 1.95 2.21 2000 1.00 a[6] 1.69 0.00 0.14 1.42 1.59 1.69 1.78 1.98 2000 1.00 a[7] 1.92 0.00 0.15 1.66 1.82 1.92 2.02 2.22 2000 1.00 a[8] 1.91 0.00 0.14 1.66 1.81 1.90 2.01 2.18 2000 1.00 a[9] 1.62 0.00 0.12 1.40 1.54 1.62 1.69 1.86 2000 1.00 a[10] 1.91 0.00 0.13 1.67 1.82 1.90 1.99 2.18 2000 1.00 a[11] 1.89 0.00 0.12 1.66 1.80 1.89 1.97 2.13 2000 1.01 a[12] 1.91 0.00 0.12 1.69 1.82 1.90 1.99 2.17 2000 1.00 a[13] 1.73 0.00 0.12 1.52 1.65 1.73 1.81 1.96 2000 1.01 a[14] 1.79 0.00 0.11 1.58 1.71 1.79 1.86 2.01 2000 1.00 a[15] 1.71 0.00 0.11 1.49 1.63 1.70 1.78 1.93 2000 1.00 a[16] 1.65 0.00 0.11 1.44 1.57 1.65 1.72 1.88 2000 1.00 a[17] 1.61 0.00 0.12 1.38 1.53 1.61 1.70 1.86 2000 1.01 a[18] 1.74 0.00 0.13 1.50 1.65 1.74 1.84 2.01 2000 1.00 a[19] 1.91 0.00 0.16 1.62 1.80 1.90 2.01 2.24 1332 1.00 a[20] 1.58 0.00 0.14 1.31 1.48 1.57 1.67 1.86 2000 1.00 a[21] 1.63 0.00 0.16 1.32 1.52 1.63 1.73 1.94 1601 1.00 a[22] 1.89 0.00 0.21 1.51 1.75 1.88 2.03 2.34 2000 1.00 a[23] 1.67 0.00 0.19 1.30 1.54 1.67 1.80 2.05 2000 1.00 a[24] 1.72 0.00 0.21 1.35 1.57 1.71 1.86 2.17 2000 1.00 a[25] 1.18 0.00 0.22 0.76 1.02 1.17 1.31 1.62 2000 1.00 b[1] 3.27 0.01 0.39 2.68 2.99 3.21 3.48 4.19 797 1.00 b[2] 2.73 0.01 0.25 2.32 2.56 2.71 2.88 3.26 1081 1.00 b[3] 2.60 0.01 0.21 2.25 2.45 2.58 2.73 3.06 1233 1.00 b[4] 2.09 0.00 0.12 1.87 2.01 2.09 2.17 2.36 1170 1.01 b[5] 1.82 0.00 0.10 1.62 1.75 1.81 1.88 2.03 925 1.00 b[6] 1.68 0.00 0.10 1.50 1.61 1.67 1.74 1.88 999 1.00 b[7] 1.35 0.00 0.07 1.21 1.30 1.34 1.39 1.49 877 1.00 b[8] 1.17 0.00 0.06 1.05 1.13 1.17 1.21 1.30 719 1.00 b[9] 0.94 0.00 0.06 0.82 0.90 0.94 0.98 1.06 876 1.00 b[10] 0.68 0.00 0.05 0.58 0.65 0.68 0.71 0.78 630 1.00 b[11] 0.43 0.00 0.05 0.34 0.40 0.43 0.46 0.52 394 1.00 b[12] 0.17 0.00 0.04 0.08 0.14 0.17 0.20 0.25 620 1.00 b[13] -0.02 0.00 0.05 -0.11 -0.05 -0.01 0.02 0.08 756 1.00 b[14] -0.26 0.00 0.05 -0.35 -0.29 -0.26 -0.23 -0.17 670 1.01 b[15] -0.46 0.00 0.05 -0.56 -0.49 -0.46 -0.42 -0.36 529 1.01 b[16] -0.73 0.00 0.05 -0.84 -0.76 -0.73 -0.69 -0.62 799 1.01 b[17] -1.10 0.00 0.07 -1.24 -1.15 -1.10 -1.06 -0.97 776 1.01 b[18] -1.21 0.00 0.07 -1.35 -1.26 -1.21 -1.16 -1.07 926 1.01 b[19] -1.43 0.00 0.08 -1.58 -1.48 -1.43 -1.37 -1.29 1034 1.00 b[20] -1.80 0.00 0.11 -2.05 -1.87 -1.80 -1.73 -1.60 1157 1.00 b[21] -2.11 0.00 0.14 -2.41 -2.20 -2.11 -2.01 -1.87 1296 1.00 b[22] -2.20 0.00 0.14 -2.50 -2.29 -2.19 -2.10 -1.95 1006 1.01 b[23] -2.53 0.01 0.19 -2.96 -2.64 -2.50 -2.40 -2.20 1279 1.00 b[24] -2.54 0.00 0.19 -2.95 -2.65 -2.52 -2.41 -2.20 1539 1.00 b[25] -3.95 0.01 0.63 -5.43 -4.27 -3.85 -3.50 -3.02 2000 1.00 |
warmup=200でも収束はうまくいっているようでした。もしうまくいっていなかったら、warmupの数を増やし、それにあわせてiterも増やしていくといいです。
事後分布なんかを図示するには、bayesplotパッケージが便利です。以下、パイプ演算子を使って図示してみます。パイプ演算子を使うと、サイズの大きいオブジェクトを増やすことなく図だけ表示できるので便利です。
|
1 2 |
library(dplyr) fit.irt %>% as.array %>% mcmc_dens(pars="a[1]") |
bayesplotパッケージは、一度配列に直さないといけませんが、それもパイプを使うと簡単です。あと、パラメータaを全部表示したい場合は、次のようにするといいです。正規表現を使います。
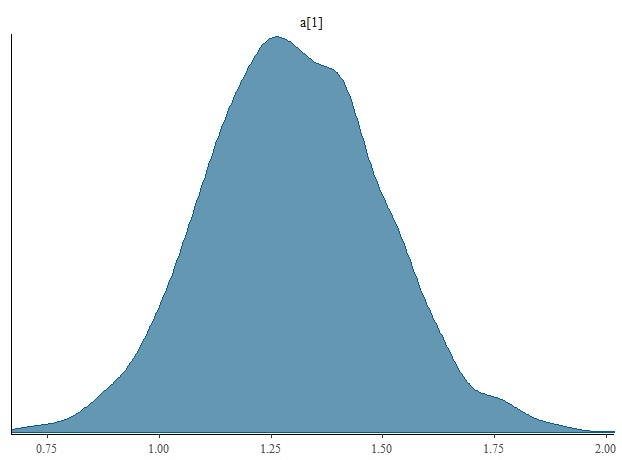
|
1 |
fit.irt %>% as.array %>% mcmc_dens(repex_pars="^a") |
こうすると、変数でaからはじまるやつ全部を図示する、ということになります。
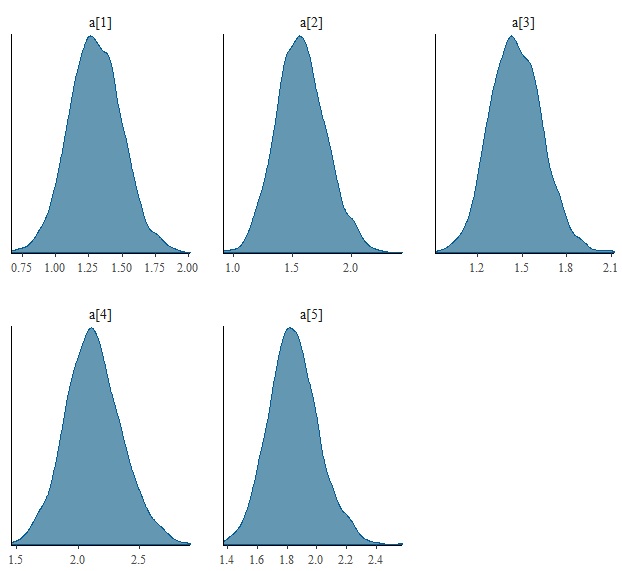
あと、a[1]からa[5]だけ図示したい場合は、たとえばdplyrを使ってこんな感じでできます。たぶんもっとおしゃれにやる方法はあると思います。
|
1 |
fit.irt %>% as.data.frame %>% select(`a[1]`:`a[5]`) %>% mcmc_dens |
項目反応関数を描画する
IRTの結果を知るのに、項目反応関数を一気に見たいことがあります。その場合は、ggplot2を使うと便利です。ここではそれ以外にもtidyrというパッケージも使っています。
なお、パラメータをstanfitオブジェクトから取り出すとき、いろんなやり方があると思いますが、僕は結局extractとapplyを使うのが早いかな・・・と思っています。もちろん、dplyrを使ったりするのもいいと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
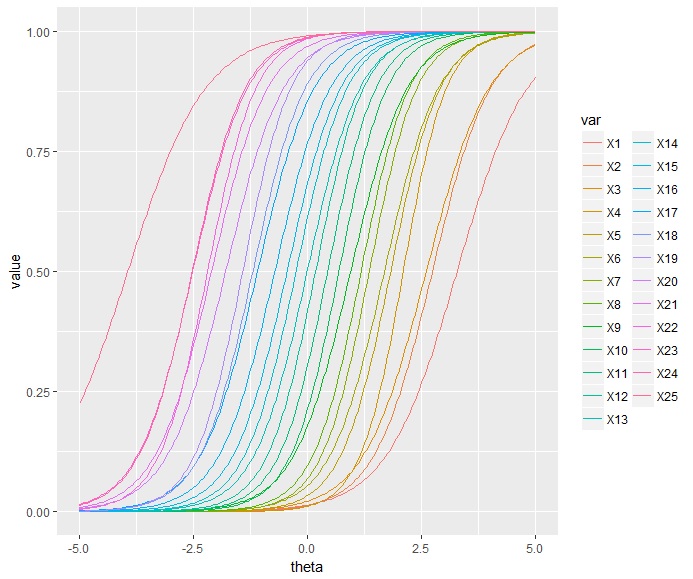
library(tidyr) #extract fit.irt <- fit.mcmc a <- rstan::extract(fit.irt)$a %>% apply(2,mean) b <- rstan::extract(fit.irt)$b %>% apply(2,mean) #dataframe for ggplot2 theta <- seq(-5,5,length.out=201) ggdf <- data.frame(matrix(ncol=P,nrow=201)) for(i in 1:P){ ggdf[,i] <- logistic(a[i]*(theta-b[i])) } ggdf$theta <- theta #ggplot2 ggdf <- ggdf %>% tidyr::gather(key=var,value,-theta,factor_key=TRUE) %>% ggplot(aes(x=theta)) ggdf + geom_line(aes(y=value,color=var)) |
こんな感じの図が得られます。
長くなったのでここで一度終わります。テスト情報関数を描画したりする方法とかは、また後日アップします。