この記事は,Stan Advent Calendar 2017の6日目の記事です。
今日はカテゴリカル因子分析をStanでやってしまおう,という記事です。
カテゴリカル因子分析とは
カテゴリカル因子分析とは,順序尺度で測定されたデータを使って因子分析をしたいときに使う方法です。過去に書いた記事がありますので,詳しくはそちらを御覧ください。
カテゴリカル因子分析は,上の記事にもあるように,重み付き最小二乗法で解くことが多いです。重み付き最小二乗法は,まずポリコリック相関行列をデータから求めて,その相関行列を標準誤差行列の逆行列で重みづけながら最小二乗法で解くという二段階の推定を行います。一致性はありますが,二段階で解く(正確には閾値を求めてから相関を計算するので3段階)というのはスマートではない感じがします(あくまで個人的感想です)。
最尤法で一気に解けないことはないですが,因子数が多くなったり,項目数が多いと重積分の計算が大変になって,その数値計算の近似精度も悪くなっていきます。
重み付き最小二乗法でも,もちろん悪くはないのですが,確率モデルをベイズでそのまま解くことができる方が,ほら,なんていうか,気持ちいいですよね(おい
というわけで,Stanでカテゴリカル因子分析をやってみたいと思います。
ついでに,過去に多次元項目反応理論をStanでやってみよう,という記事を去年のStanアドカレで書いています。
これで似たような分析はできるんですが,このコードをMCMCで実行すると2~3日かかることがあります。めちゃくちゃ時間かかるんです。変分ベイズなら1時間程度で終わりますが,変分ベイズはStanでもそれほど推奨されてない(むしろ推奨してない)ので微妙なところです。
そこで今日は,前日の記事であるポリコリック相関係数を利用したカテゴリカル因子分析をやってみます。そうすると,MCMCでも(項目数によりますが),1時間~3時間ぐらいで終わります。すごい!速い!(あくまで相対的な意味で)。なぜこんなに速くなるかというと,ポリコリック相関を使ったカテゴリカル因子分析は十分統計量としてクロス表を利用できます。よって,フルのデータを使って分析するIRTに比べて非常に高速です。高速といってもまぁ1時間はかかるんですが。
未読の方は昨日のアドカレ記事も合わせて見ていただけるといいかと思います。
サンプルデータ
今回もサンプルデータはpsychパッケージに入ってるbfiにします。ただ,データがでかいのと項目数が多くて時間がかかるので,500人15項目に減らします。この15項目は理論上3因子に分かれるはずです。
ついでに今回使うパッケージも一緒に読み込みます。rstanはもちろん,psychとdplyrを入れておきます。でもパイプ演算子を使いたいだけなので,magrittrパッケージだけでもOKです。
|
1 2 3 4 5 6 7 |
library(rstan) library(psych) library(GPArotation) library(dplyr) set.seed(123) dat <- na.omit(bfi)[sample(1:nrow(na.omit(bfi)),500),1:15] |
psychパッケージのirt.fa()関数でやってみます。これはポリコリック相関行列+minres法の結果です。本来は標準誤差行列の逆行列で重み付け無いと一致推定量にならないのですが,psychの関数ではそこまではやってくれません。3因子でオブリミン回転をしてみます。
|
1 2 |
result <- irt.fa(dat,nfactors=3,rotate="oblimin") result$fa |
結果は以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
Factor Analysis using method = minres Call: fa(r = r, nfactors = nfactors, n.obs = n.obs, rotate = rotate, fm = fm) Standardized loadings (pattern matrix) based upon correlation matrix MR3 MR1 MR2 h2 u2 com A1 -0.55 0.20 0.00 0.24 0.76 1.3 A2 0.72 0.04 0.00 0.55 0.45 1.0 A3 0.80 0.02 -0.01 0.65 0.35 1.0 A4 0.49 0.07 0.10 0.33 0.67 1.1 A5 0.56 0.18 0.03 0.45 0.55 1.2 C1 -0.05 0.05 0.60 0.36 0.64 1.0 C2 0.13 -0.14 0.66 0.45 0.55 1.2 C3 0.04 -0.02 0.56 0.33 0.67 1.0 C4 0.05 -0.04 -0.72 0.52 0.48 1.0 C5 0.01 -0.12 -0.55 0.35 0.65 1.1 E1 0.04 -0.64 0.13 0.36 0.64 1.1 E2 0.02 -0.78 -0.03 0.60 0.40 1.0 E3 0.27 0.42 0.09 0.40 0.60 1.8 E4 0.19 0.70 -0.02 0.65 0.35 1.2 E5 -0.04 0.55 0.25 0.41 0.59 1.4 MR3 MR1 MR2 SS loadings 2.30 2.24 2.10 Proportion Var 0.15 0.15 0.14 Cumulative Var 0.15 0.30 0.44 Proportion Explained 0.35 0.34 0.32 Cumulative Proportion 0.35 0.68 1.00 With factor correlations of MR3 MR1 MR2 MR3 1.00 0.47 0.30 MR1 0.47 1.00 0.27 MR2 0.30 0.27 1.00 |
ついでに,Mplusでもカテゴリカル因子分析ができます。その結果も載せておきます。上のpsychの結果とそれなりに近い結果になってるのがわかると思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
-.563 .010 .212 .727 -.002 .028 .797 -.005 .028 .485 .106 .085 .567 .030 .182 -.044 .605 .043 .129 .660 -.146 .048 .558 -.025 .061 -.733 -.043 .010 -.566 -.119 .048 .127 -.649 .023 -.041 -.783 .304 .092 .407 .191 -.016 .706 -.016 .253 .529 |
カテゴリカル因子分析をStanでやる
さっそく,カテゴリカル因子分析を実行するStanコードを書いてみました。ベースとなってるのは前日の記事のポリコリック相関係数を求めるコードです。これに因子分析のコードを合わせた感じです。これをpolychoric_fa.stanというファイルに保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
functions{ real binormal_cdf(real h, real k, real rho) { if (h == 0 && k == 0) { return 0.25 + asin(rho) / (2 * pi()); }else{ real h2 = h==0 ? h + 1E-34 : h; real k2 = k==0 ? k + 1E-34 : k; real a1 = (k / h2 - rho) / sqrt((1 - rho^2)); real a2 = (h / k2 - rho) / sqrt((1 - rho^2)); real delta = h * k < 0 || (h * k == 0 && (h + k) < 0); return 0.5 * (Phi(h) + Phi(k) - delta) - owens_t(h, a1) - owens_t(k, a2); } } real polychoric(vector a, vector b, int s1, int s2, real rho){ real temp = binormal_cdf(a[s1+1],b[s2+1],rho) + binormal_cdf(a[s1],b[s2],rho); temp = temp - binormal_cdf(a[s1],b[s2+1],rho) - binormal_cdf(a[s1+1],b[s2],rho); temp = temp <= 0 ? not_a_number() : temp; return log(temp); } } data{ int P; int A; int K; int Smax; int S[P]; vector[Smax+2] thr[P]; matrix[Smax,Smax] y[P*P]; } transformed data{ matrix[Smax,Smax] x[P,P]; { int i = 0; for(p1 in 1:P){ for(p2 in 1:P){ i = i + 1; x[p1,p2] = y[i]; } } } } parameters{ real real } transformed parameters{ matrix[P,A] lambda; matrix[P,P] rho; { int i = 0; int j = 0; for(p in 1:P){ for(a in 1:A){ if(a < p){ i = i + 1; lambda[p,a] = lambda_raw[i]; }else if(a==p){ j = j + 1; lambda[p,a] = lambda_diag[j]; }else{ lambda[p,a] = 0.0; } } } } rho = lambda*lambda'; } model{ for(p1 in 1:P){ for(p2 in (p1+1):P){ int S1 = S[p1]; int S2 = S[p2]; for(s1 in 1:S1){ for(s2 in 1:S2){ if(x[p1,p2][s1,s2]!=0){ target += x[p1,p2][s1,s2] * polychoric(thr[p1],thr[p2],s1,s2,rho[p1,p2]); } } } } } lambda_raw ~ uniform(-1,1); lambda_diag ~ uniform(0,1); } |
コードのポイントは,因子負荷量は-1~1の範囲に収まるようにしています。こうしないと,相関行列が1を超えてしまい,尤度の計算ができなくなってしまうからです。因子負荷量の制約の書け方については,去年の小杉先生のアドカレ記事を見ていただけたら何となく分かると思います。
これを実行するためのRコードを関数化しました。fa.poly.stan()です。psychパッケージにfa.poly関数がある(もうdeprecatedみたいですが)ので,それをもじってみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
fa.poly.stan <- function(data,model,nfactors=1,iter=2000,warmup=NULL,chains=4,cores=4){ if(is.null(warmup)) warmup <- iter/2 model = model.fa P <- ncol(data) S <- c() for(i in 1:P) S[i] <- length(table(data[,i])) Smax <- max(S) #threshold thr <- list() af <- 8 for(p in 1:P){ temp <- qnorm(cumsum(table(data[,p])/length(data[,p])))[-S[p]] thr[[p]] <- c(-af,temp,af,rep(99,Smax-S[p]+1)) } #cross table y <- list() i <- 0 for(p1 in 1:P){ for(p2 in 1:P){ i <- i +1 x <- matrix(rep(99,Smax^2),nrow=Smax,ncol=Smax) x[1:S[p1],1:S[p2]] <- table(data[,p1],data[,p2]) y[[i]] <- x } } #data for Stan A <- nfactors K=P*A-(A^2-A)/2 data.fa <- list(P=P,A=A,K=K,Smax=Smax,S=S,thr=thr,y=y) #initial values for Stan temp <- t(chol(cor(dat))) lambda_diag <- diag(temp[,1:A]) - rep(0.2,A) lambda_raw <- temp[,1:A][lower.tri(temp[,1:A])] init.vb <- list(lambda_raw=lambda_raw,lambda_diag=lambda_diag) init.fa <- list() for(c in 1:1) init.fa[[c]] <- init.vb #sampling cat("initial model start.\n") fit.ini <- sampling(model,data=data.fa,init=init.fa, iter=200,warmup=100,chains=1,cores=1) cat("MCMC sampling start.\n") lambda_diag <- apply(rstan::extract(fit.ini)$lambda_diag,2,mean) lambda_raw <- apply(rstan::extract(fit.ini)$lambda_raw,2,mean) init.vb <- list(lambda_raw=lambda_raw,lambda_diag=lambda_diag) init.fa <- list() for(c in 1:chains) init.fa[[c]] <- init.vb fit <- sampling(model,data=data.fa,init=init.fa, iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit) } |
中で少し工夫をしています。まず,因子分析は初期値の設定が大事です。因子分析は解が正負逆転しても成り立つので,符号についての不定性があるのです。なので,MCMCが正側に行くか負側に行くかは,初期値に大きく依存します。よって,初期値をすべてのチェインで同じにしておく必要があるのです。
できるだけ事後分布に近い初期値にするために,まず相関行列をコレスキー分解したものの一部を使って1つのチェインで200回分だけ走らせます。そして,その解を4つのチェインの初期値にしてもう一回走らせる,というまぁ面倒なことをやっています。
最尤法や最小二乗法の結果を入れたらええがな!と思われるかもですが,R上でええ感じにやってくれる関数がないこと,またStanで因子負荷量を推定するためにはちょっと因子負荷行列に制約を与えないといけないことなどがあって,上手くいかないのです。というわけで今回は上のような処理をやってみました。
上の関数を読み込んでおけば,実際に実行するRコードは下のものだけでいけます。
|
1 2 3 4 5 |
fit <- fa.poly.stan(dat,model,nfactors=3,chains=4,cores=4) print(fit,pars="lambda") stan_dens(fit,pars="lambda[1,1]",separate_chains = T) stan_trace(fit,pars="lambda[1,1]") |
結果は以下になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
Inference for Stan model: polychoric_fa. 4 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=4000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat lambda[1,1] 0.46 0.00 0.05 0.37 0.43 0.46 0.49 0.55 1101 1.00 lambda[1,2] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 4000 NaN lambda[1,3] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 4000 NaN lambda[2,1] -0.66 0.00 0.05 -0.75 -0.69 -0.66 -0.63 -0.57 1682 1.00 lambda[2,2] 0.27 0.00 0.07 0.14 0.23 0.28 0.32 0.39 616 1.00 lambda[2,3] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 4000 NaN lambda[3,1] -0.76 0.00 0.05 -0.86 -0.79 -0.76 -0.73 -0.66 1489 1.00 lambda[3,2] 0.29 0.00 0.08 0.12 0.24 0.29 0.34 0.42 598 1.00 lambda[3,3] 0.05 0.00 0.04 0.00 0.02 0.04 0.07 0.14 2368 1.00 lambda[4,1] -0.49 0.00 0.05 -0.58 -0.52 -0.49 -0.46 -0.39 1806 1.00 lambda[4,2] 0.27 0.00 0.06 0.14 0.24 0.28 0.31 0.38 578 1.00 lambda[4,3] -0.07 0.00 0.06 -0.17 -0.11 -0.07 -0.04 0.05 810 1.01 lambda[5,1] -0.57 0.00 0.05 -0.66 -0.60 -0.57 -0.53 -0.47 1178 1.00 lambda[5,2] 0.37 0.00 0.07 0.23 0.33 0.37 0.41 0.48 385 1.01 lambda[5,3] 0.01 0.00 0.06 -0.11 -0.03 0.01 0.05 0.14 789 1.01 lambda[6,1] -0.10 0.00 0.06 -0.22 -0.14 -0.10 -0.05 0.03 1038 1.00 lambda[6,2] 0.23 0.01 0.13 -0.03 0.14 0.23 0.32 0.48 511 1.01 lambda[6,3] -0.51 0.01 0.10 -0.62 -0.56 -0.53 -0.49 -0.32 252 1.02 lambda[7,1] -0.24 0.00 0.06 -0.36 -0.29 -0.25 -0.20 -0.12 888 1.01 lambda[7,2] 0.12 0.01 0.15 -0.16 0.02 0.12 0.22 0.41 503 1.02 lambda[7,3] -0.58 0.01 0.09 -0.67 -0.62 -0.59 -0.55 -0.45 240 1.01 lambda[8,1] -0.16 0.00 0.06 -0.27 -0.20 -0.16 -0.12 -0.05 989 1.01 lambda[8,2] 0.18 0.01 0.13 -0.07 0.10 0.18 0.26 0.42 504 1.02 lambda[8,3] -0.49 0.01 0.09 -0.59 -0.54 -0.50 -0.47 -0.35 241 1.02 lambda[9,1] 0.10 0.00 0.06 -0.03 0.05 0.10 0.14 0.22 871 1.01 lambda[9,2] -0.27 0.01 0.16 -0.58 -0.38 -0.28 -0.17 0.04 497 1.01 lambda[9,3] 0.64 0.01 0.12 0.41 0.60 0.66 0.70 0.77 243 1.02 lambda[10,1] 0.13 0.00 0.06 0.02 0.09 0.13 0.17 0.24 906 1.01 lambda[10,2] -0.30 0.01 0.13 -0.52 -0.38 -0.31 -0.22 -0.05 500 1.01 lambda[10,3] 0.48 0.01 0.11 0.26 0.43 0.49 0.54 0.60 278 1.02 lambda[11,1] 0.02 0.00 0.06 -0.10 -0.02 0.02 0.06 0.14 814 1.00 lambda[11,2] -0.55 0.01 0.10 -0.66 -0.60 -0.57 -0.53 -0.39 233 1.03 lambda[11,3] -0.18 0.01 0.14 -0.45 -0.27 -0.18 -0.08 0.10 517 1.01 lambda[12,1] 0.10 0.00 0.08 -0.04 0.05 0.10 0.15 0.26 692 1.00 lambda[12,2] -0.75 0.01 0.11 -0.84 -0.79 -0.76 -0.73 -0.62 208 1.02 lambda[12,3] -0.05 0.01 0.18 -0.42 -0.17 -0.05 0.08 0.28 472 1.02 lambda[13,1] -0.36 0.00 0.06 -0.48 -0.40 -0.36 -0.32 -0.24 877 1.00 lambda[13,2] 0.50 0.00 0.07 0.38 0.48 0.51 0.54 0.60 268 1.01 lambda[13,3] -0.03 0.00 0.10 -0.22 -0.10 -0.03 0.04 0.19 525 1.02 lambda[14,1] -0.28 0.00 0.07 -0.43 -0.32 -0.28 -0.23 -0.14 694 1.00 lambda[14,2] 0.72 0.01 0.10 0.57 0.70 0.74 0.77 0.82 212 1.02 lambda[14,3] 0.10 0.01 0.16 -0.21 -0.02 0.09 0.20 0.42 500 1.02 lambda[15,1] -0.12 0.00 0.07 -0.25 -0.16 -0.12 -0.07 0.01 863 1.00 lambda[15,2] 0.57 0.01 0.09 0.43 0.54 0.58 0.61 0.67 272 1.01 lambda[15,3] -0.16 0.01 0.14 -0.40 -0.26 -0.17 -0.08 0.14 427 1.02 |
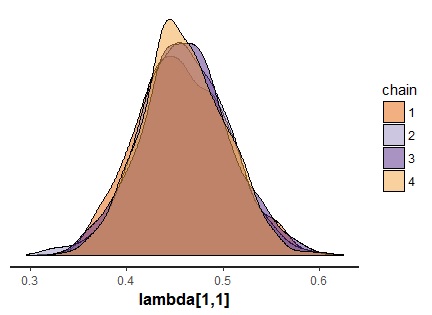
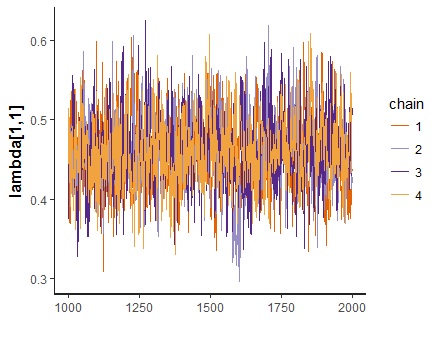
一応なんとか収束していますが,若干自己相関が残ってる感じもします。今回は4000回サンプリングしてますが,もう少し多くてもいいかもしれません。
もしRhatがとても大きいもの(5とか)があった場合,多峰性を疑ってみてください。それはチェインによって収束した符号が違ってる場合に起きます。あとでチェインごとに正負をひっくり返してもいいのですが,できれば初期値をそろえて走らせたほうが面倒がなくていいと思います。
さて,得られたlambdaは制約入りの因子負荷量で,いわゆる初期解みたいなものです。これを回転して,解釈がし易い因子負荷量行列になります。
事後分布そのものを回転させることもできますが,それはまたの機会として,今回は初期解の中央値だけを回転してみます。上のMplusの結果とだいたい似ているのがわかると思います。
|
1 |
fit %>% rstan::extract() %$% lambda %>% apply(c(2,3),median) %>% oblimin |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
Oblique rotation method Oblimin Quartimin converged. Loadings: [,1] [,2] [,3] [1,] 0.52003 0.1812 -0.00747 [2,] -0.69838 0.0209 -0.02408 [3,] -0.81453 0.0114 0.02560 [4,] -0.48603 0.0694 -0.10189 [5,] -0.57458 0.1600 -0.02550 [6,] 0.03765 0.0395 -0.56810 [7,] -0.13656 -0.1459 -0.61916 [8,] -0.05196 -0.0296 -0.53966 [9,] -0.06857 -0.0489 0.70408 [10,] -0.00733 -0.1134 0.53771 [11,] -0.05139 -0.6242 -0.11512 [12,] -0.02024 -0.7509 0.04088 [13,] -0.30650 0.3730 -0.09080 [14,] -0.19404 0.6708 0.01315 [15,] 0.00946 0.4961 -0.24252 Rotating matrix: [,1] [,2] [,3] [1,] 1.132 0.394 -0.0163 [2,] 0.191 1.040 -0.1284 [3,] -0.201 0.307 1.0538 Phi: [,1] [,2] [,3] [1,] 1.000 -0.481 0.304 [2,] -0.481 1.000 -0.272 [3,] 0.304 -0.272 1.000 |
因子得点の推定
カテゴリカル因子分析は,因子構造を知るだけでなく,因子得点の計算も必要になります。なぜなら,このあと尺度平均値で因子得点を求めてしまったら,わざわざ時間を書けてまで順序尺度を仮定した分析を行った意味が半減してしまうからです。
というわけで,上で求めた因子負荷量行列を入れたら因子得点をカテゴリカル因子分析のモデルでMCMC推定するStanコードも書いてみました。
こちらは上のコードとは違って純粋にサンプルサイズに計算時間が依存します。500人ぐらいでも4000回で1時間ぐらいかかるかなと思うので,上と合わせて2~3時間はかかる計算になりますね。根気とStanへの愛が試されます。
Stanコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
data{ int N; int P; int A; matrix[P,A] lambda; matrix[A,A] rho; int Smax; int S[P]; vector[Smax+2] thr[P]; int y[N,P]; } transformed data{ vector[A] lambda2[P]; vector[P] theta; for(p in 1:P){ for(a in 1:A){ lambda2[p][a] = lambda[p,a]; } } theta = rep_vector(1,P) - diagonal(lambda*lambda'); } parameters{ vector[A] score[N]; } model{ for(n in 1:N){ for(p in 1:P){ target += log(Phi(thr[p,y[n,p]+1]-lambda2[p]'*score[n])/theta[p]^0.5 -Phi(thr[p,y[n,p]]-lambda2[p]'*score[n])/theta[p]^0.5); } } score ~ multi_normal(rep_vector(0,A),rho); } |
途中,コメントアウトみたいになってますが,Stanでは転置の演算子が ’ なので,こうなってしまってます。このまま貼り付けてもらえればStanではちゃんと動きます。
次に,Stanコードを実行させるための関数を作りました。fa.poly.stan.score()です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
fa.poly.stan.score <- function(data,model,fit,rotate="oblimin",iter=2000,warmup=NULL,chains=4,cores=4){ if(is.null(warmup)) warmup <- iter/2 model.fs <- model lambda <- apply(rstan::extract(fit)$lambda,c(2,3),median) lambda <- do.call(rotate,list(lambda)) N <- nrow(data) A <- ncol(lambda$loadings) P <- nrow(lambda$loadings) S <- c() for(i in 1:P) S[i] <- length(table(data[,i])) Smax <- max(S) #threshold thr <- list() af <- 8 for(p in 1:P){ temp <- qnorm(cumsum(table(data[,p])/length(data[,p])))[-S[p]] thr[[p]] <- c(-af,temp,af,rep(99,Smax-S[p]+1)) } #data for Stan data.fs <- list(N=N,A=A,P=P,S=S,Smax=Smax,thr=thr,lambda=lambda$loadings, rho=lambda$Phi,y=data) #initial value for Stan C <- chains init.fs <- list() for(i in 1:C){ init.fs[[i]] <- list(score=matrix(rep(0,N*A),ncol=A,nrow=N)) } cat("MCMC sampling start.\n") fit.fs <- sampling(model.fs,data=data.fs,init=init.fs, iter=2000,warmup=1000,chains=C,cores=C) return(fit.fs) } |
この関数を下のコードで実行すれば,因子得点を得ることができます。今回は2000回で少なめにしています。
関数の引数は,データ,モデル,fa.poly.stanが出したstanfitオブジェクト,回転方法などなどです。今回はオブリミン回転を使ってますが,Promaxと書けばプロマックス回転になります。詳しくはGPArotationパッケージの説明を見てください。
一応収束を確認しましょう。
|
1 |
stan_rhat(fit.fs,pars="score") |
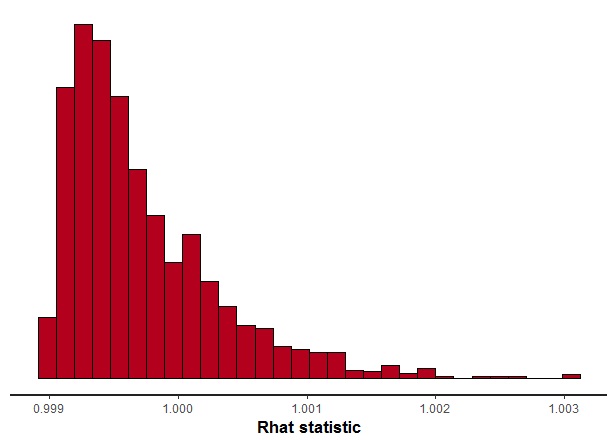
一番悪くても1.003と,とてもキレイに収束していました。
また,Mplusで計算した因子得点との相関係数を出してみましょう。
|
1 2 3 4 5 6 7 8 9 10 |
fit.fs <- fa.poly.stan.score(dat,model.fs,fit,rotate="oblimin",chains=2,cores=2) score.stan <- fit.fs %>% rstan::extract() %$% score %>% apply(c(2,3),median) score.mplus <- read.csv("score_mplus.csv") cor(score,score.mplus) |
結果は下のような感じ。回転によって因子の場所がズレてますが,該当する因子同士の相関は0.99を超えています。推定はちゃんとできていそうです。
|
1 2 3 4 |
Mplus1 Mplus2 Mplus3 [1,] -0.9912253 -0.4267827 -0.6285197 [2,] 0.6246837 0.3951640 0.9915592 [3,] -0.4153754 -0.9961524 -0.3924276 |
というわけで,カテゴリカル因子分析をMCMCで推定する方法についてまとめました。カテゴリカル因子分析をベイズでやる意味は・・・あまりないかもしれなけど,最尤法で不適解が出たときとの選択肢としてあるといいかなと思います。時間は結構かかりますけど。
Enjoy!