この記事はStan Advent Calendar2017の5日目の記事です。
今回は,Stanでポリコリック相関係数を推定するという内容です。
ポリコリック相関係数とは
ポリコリック相関係数は,順序性があるカテゴリカルデータ同士の相関係数の一種です。順序性のあるカテゴリカル・データのための相関係数といえばスピアマンの順位相関とか,ケンドールの順位相関がありますが,ポリコリック相関係数はパラメトリックな方法なので確率モデルを定義して,ベイズ推定も可能です。
ポリコリック相関係数については以前書いた記事があるのでそちらを見てもらえると早いです。
簡単に言えば,順序データの背後に連続的な変数があると想定します。得られたデータは本来は連続的な値をとる性質をもつ変数なんだけど,データとしてはカテゴリカルになってしまった,とかそういう想定です。で,背後にある真の連続値同士の相関を推定しましょう,というのがポリコリック相関係数というわけです。
具体的には,心理尺度なんかが典型的です。心理尺度では態度を5段階評定で測定したりしますが,間隔が等しいという仮定が満たされない場合は順序尺度データとして扱わざるをえない時があります。そういうときにポリコリック相関係数を使うと,より妥当な相関関係を推定できると考えられています。
ポリコリック相関係数の確率モデル
ポリコリック相関係数は,背後に仮定される連続的な値が,推定したい相関係数を持つ二変量正規分布に従うと考えます。そして,それがカテゴリの閾値に従ってクロス表として実現するという想定です。なのでデータとして使うのもクロス表です。推定するのは,相関係数と閾値です。
このあたりの確率モデルについては,小杉先生の資料がとてもわかりやすくて参考になります。
確率モデルは,次のようになります。
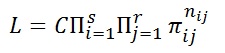
ここで,i,jはクロス表の行列を表す添字で,nはクロス表における各セルの人数です。πはセルに所属する確率です。このπは,背後にある連続変量が二変量正規分布に従う場合,次のように計算できます。
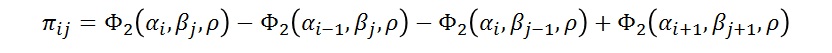
ここで,Φ2()は二変量累積正規関数,α,βは変数1,変数2の閾値パラメータ,ρはポリコリック相関係数です。
確率モデルは以上で,あとはαとβに適当な無情報事前分布を,ρにlkj_corr()などで事前分布を仮定すればベイズ推定が可能です。
ただし・・・
実は,Stan2.17現在では,二変量累積正規関数はStanには入っていません。なので自分で定義しないといけないわけです。
いろいろ論文を調べると,二変量累積正規関数は,Owenのt関数を使って計算できるようです。この論文の式(4)がそれです。
幸いにも,StanにはOwenのt関数が最初から入ってるのでそれを使えば比較的簡単に実装できそうですね。
そして世の中にはすごい人がいろいろいるもんで,Stanの掲示板に二変量累積正規関数を作ってあげてくれている人がいました。いやーありがたい。
https://github.com/stan-dev/stan/issues/2356
ただ,このままだと推定上うまくいかないこともあたったので,ちょっと修正して使っています。
リンク先を見ると,将来的にはStanにも二変量累積正規関数が正式に実装されそうです。
ポリコリック相関係数を計算するためのコード
それでは早速ポリコリック相関係数を推定するためのStanコードを書いてみます。以下のようになります。これをpolychoric.stanというファイルに保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
functions{ real binormal_cdf(real h, real k, real rho) { if (h == 0 && k == 0) { return 0.25 + asin(rho) / (2 * pi()); }else{ real h2 = h==0 ? h + 1E-34 : h; real k2 = k==0 ? k + 1E-34 : k; real a1 = (k / h2 - rho) / sqrt((1 - rho^2)); real a2 = (h / k2 - rho) / sqrt((1 - rho^2)); real delta = h * k < 0 || (h * k == 0 && (h + k) < 0); return 0.5 * (Phi(h) + Phi(k) - delta) - owens_t(h, a1) - owens_t(k, a2); } } real polychoric(vector a, vector b, int s1, int s2, real rho){ real temp = binormal_cdf(a[s1+1],b[s2+1],rho) + binormal_cdf(a[s1],b[s2],rho); temp = temp - binormal_cdf(a[s1],b[s2+1],rho) - binormal_cdf(a[s1+1],b[s2],rho); temp = temp <= 0 ? not_a_number() : temp; return log(temp); } } data{ int S1; int S2; real absinf; int y[S1,S2]; } parameters{ ordered[S1-1] thr1; ordered[S2-1] thr2; real } transformed parameters{ vector[S1+1] a; vector[S2+1] b; for(s1 in 2:S1){ a[s1] = thr1[s1-1]; } a[1] = -absinf; a[S1+1] = absinf; for(s2 in 2:S2){ b[s2] = thr2[s2-1]; } b[1] = -absinf; b[S2+1] = absinf; } model{ for(s1 in 1:S1){ for(s2 in 1:S2){ if(y[s1,s2]!=0){ target += y[s1,s2] * polychoric(a,b,s1,s2,rho); } } } thr1 ~ normal(0,5); thr2 ~ normal(0,5); rho ~ uniform(-1,1); } |
今回使うパッケージは以下です。ここにまとめておきます。
|
1 2 3 |
library(rstan) library(psych) library(dplyr) |
これを,次のRで実行するコードは以下です。ちょっと長くなるので関数化しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
polycorr.stan <- function(data,model,iter=4000,warmup=NULL,chains=4,cores=1){ if(is.null(warmup)) warmup = iter/2 S1 = nrow(table(data)) S2 = ncol(table(data)) absinf <- 5 thr1 = qnorm(cumsum(table(data[,1])/length(data[,1])))[-S1] thr2 = qnorm(cumsum(table(data[,2])/length(data[,2])))[-S2] data.poly <- list(S1=S1,S2=S2,absinf=absinf,y=table(data)) init.vb <- list(a=thr1,b=thr2,rho=cor(data)[1,2]) init.poly <- list() for(c in 1:chains) init.poly[[c]] <- init.vb cat("MCMC sampling start.\n") fit.poly <- sampling(model,data=data.poly,init=init.poly, iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.poly) } |
コアは適宜環境に合わせて複数に変えてください。iterとwarmup,chainsも引数で変えられます。
Rコードを見てもらえればわかるように,閾値の初期値は累積正規関数(qnorm)で計算しています。
この関数の使い方は,次のような感じ。なお,データはpsychパッケージのbfiというデータセットから最初の2変数だけ取り出しています。
|
1 2 3 4 5 6 7 |
data(bfi) dat <- na.omit(bfi[1:2]) model.poly <- stan_model("polychoric.stan") fit <- polycorr.stan(dat,model.poly,cores=1) print(fit,pars=c("rho","thr1","thr2")) |
まずStanコードをコンパイルして,model.polyにいれます。一度コンパイルすればどんなデータでも同じモデルでできるので,サクサクです。
それとデータを引数にしてpolycorr.stan関数に入れます。戻り値はStanfitクラスのオブジェクトなので,いつものように結果の中身を見ます。相関係数はrho,閾値はthr1とthr2というパラメータ名で取り出せます。
推定時間は僕のPCで4000回のサンプリングで33秒ほどでした。データはクロス表を入れているので,実はサンプルサイズが大きくなってもほとんど推定時間は変わりません。逆に,カテゴリ数(つまりクロス表のセル数)が大きくなると推定時間が長くなります。
結果は以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Inference for Stan model: polychoric. 4 chains, each with iter=4000; warmup=2000; thin=1; post-warmup draws per chain=2000, total post-warmup draws=8000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat rho -0.41 0 0.02 -0.45 -0.42 -0.41 -0.40 -0.37 8000 1 thr1[1] -0.44 0 0.02 -0.49 -0.45 -0.44 -0.42 -0.39 5739 1 thr1[2] 0.33 0 0.02 0.28 0.32 0.33 0.35 0.38 8000 1 thr1[3] 0.75 0 0.03 0.70 0.73 0.75 0.76 0.80 8000 1 thr1[4] 1.23 0 0.03 1.16 1.20 1.23 1.25 1.29 8000 1 thr1[5] 1.86 0 0.05 1.77 1.83 1.86 1.89 1.95 8000 1 thr2[1] -2.12 0 0.06 -2.23 -2.16 -2.12 -2.08 -2.01 4736 1 thr2[2] -1.54 0 0.04 -1.61 -1.56 -1.54 -1.51 -1.47 8000 1 thr2[3] -1.19 0 0.03 -1.25 -1.21 -1.19 -1.17 -1.13 8000 1 thr2[4] -0.48 0 0.02 -0.52 -0.49 -0.48 -0.46 -0.43 8000 1 thr2[5] 0.48 0 0.02 0.44 0.47 0.48 0.50 0.53 8000 1 |
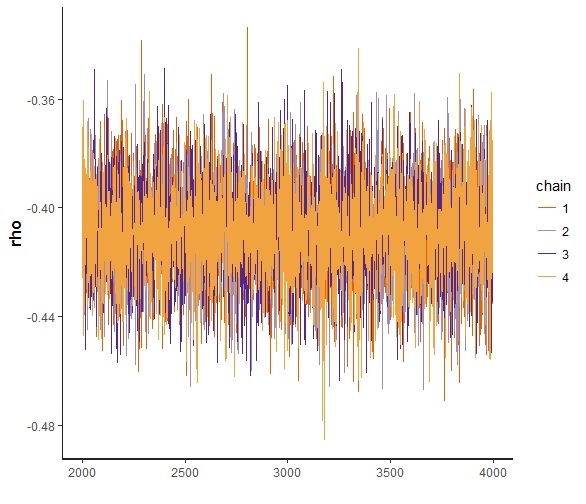
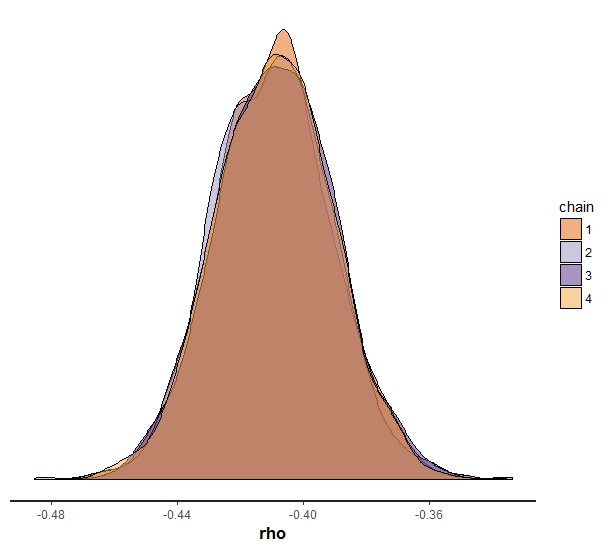
ちゃんと収束してそうです。
ついでに,psychパッケージにはポリコリック相関係数を出してくれるpolychoric()という関数があります。結果を比較すると,当たり前ですが一致します。
|
1 2 3 4 5 6 7 8 9 10 |
Call: polychoric(x = dat) Polychoric correlations A1 A2 A1 1.00 A2 -0.41 1.00 with tau of 1 2 3 4 5 A1 -0.44 0.32 0.74 1.23 1.90 A2 -2.12 -1.54 -1.19 -0.48 0.49 |
2step推定
さて,ポリコリック相関係数だけを知りたい場合は,閾値をデータから直接計算して,それを固定した上で相関だけを計算するということもできます。これを2step推定と呼んだりします。もちろん,すべてのパラメータを同時に推定した方がいいのですが,閾値と相関は互いにほとんど影響しあわないみたいで,2step推定でも分析精度はほとんどかわらず,むしろ推定の安定化・高速化ができます。
というわけで,2step推定をするためのStanコードを書いておきます。これをpolychoric_2step.stanというファイルに保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
functions{ real binormal_cdf(real h, real k, real rho) { if (h == 0 && k == 0) { return 0.25 + asin(rho) / (2 * pi()); }else{ real h2 = h==0 ? h + 1E-34 : h; real k2 = k==0 ? k + 1E-34 : k; real a1 = (k / h2 - rho) / sqrt((1 - rho^2)); real a2 = (h / k2 - rho) / sqrt((1 - rho^2)); real delta = h * k < 0 || (h * k == 0 && (h + k) < 0); return 0.5 * (Phi(h) + Phi(k) - delta) - owens_t(h, a1) - owens_t(k, a2); } } real polychoric(vector a, vector b, int s1, int s2, real rho){ real temp = binormal_cdf(a[s1+1],b[s2+1],rho) + binormal_cdf(a[s1],b[s2],rho); temp = temp - binormal_cdf(a[s1],b[s2+1],rho) - binormal_cdf(a[s1+1],b[s2],rho); temp = temp <= 0 ? not_a_number() : temp; return log(temp); } } data{ int S1; int S2; vector[S1+1] a; vector[S2+1] b; int y[S1,S2]; } parameters{ real } model{ for(s1 in 1:S1){ for(s2 in 1:S2){ if(y[s1,s2]!=0){ target += y[s1,s2] * polychoric(a,b,s1,s2,rho); } } } rho ~ uniform(-1,1); } |
これに対応した,関数を作りました。polycorr.stan1()です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
polycorr.stan1 <- function(data,model,iter=4000,warmup=NULL,chains=4,cores=1){ if(is.null(warmup)) warmup = iter/2 S1 = nrow(table(data)) S2 = ncol(table(data)) absinf <- 5 thr1 = c(-absinf,qnorm(cumsum(table(data[,1])/length(data[,1])))[-S1],absinf) thr2 = c(-absinf,qnorm(cumsum(table(data[,2])/length(data[,2])))[-S2],absinf) data.poly <- list(S1=S1,S2=S2,a=thr1,b=thr2,absinf=absinf,y=table(data)) init.vb <- list(rho=cor(data)[1,2]) init.poly <- list() for(c in 1:chains) init.poly[[c]] <- init.vb cat("MCMC sampling start.\n") fit.poly <- sampling(model,data=data.poly,init=init.poly, iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.poly) } |
これを次のRコードで実行します。さっきとほとんど同じです。
|
1 2 3 4 |
model.poly1 <- stan_model("polychoric_2step.stan") fit1 <- polycorr.stan1(dat,model.poly1,cores=1) print(fit1,pars="rho") |
今度は4000回のサンプリングで5秒弱になりました。結果はほぼ同じです。
|
1 2 3 4 5 6 |
Inference for Stan model: polychoric_2step. 4 chains, each with iter=4000; warmup=2000; thin=1; post-warmup draws per chain=2000, total post-warmup draws=8000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat rho -0.41 0 0.02 -0.44 -0.42 -0.41 -0.4 -0.37 2790 1 |
ポリコリック相関行列を一気に推定したい
上のコードでは1つの相関係数しか推定できませんでした。しかし,実際は複数の項目間の相関を一気に推定したいことがほとんどです。
というわけで,ポリコリック相関行列を推定するためのStanコードを書いてみました。
これをpolychoric_multi.stanというファイルに保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
functions{ real binormal_cdf(real h, real k, real rho) { if (h == 0 && k == 0) { return 0.25 + asin(rho) / (2 * pi()); }else{ real h2 = h==0 ? h + 1E-34 : h; real k2 = k==0 ? k + 1E-34 : k; real a1 = (k / h2 - rho) / sqrt((1 - rho^2)); real a2 = (h / k2 - rho) / sqrt((1 - rho^2)); real delta = h * k < 0 || (h * k == 0 && (h + k) < 0); return 0.5 * (Phi(h) + Phi(k) - delta) - owens_t(h, a1) - owens_t(k, a2); } } real polychoric(vector a, vector b, int s1, int s2, real rho){ real temp = binormal_cdf(a[s1+1],b[s2+1],rho) + binormal_cdf(a[s1],b[s2],rho); temp = temp - binormal_cdf(a[s1],b[s2+1],rho) - binormal_cdf(a[s1+1],b[s2],rho); temp = temp <= 0 ? not_a_number() : temp; return log(temp); } } data{ int P; int Smax; int S[P]; vector[Smax+2] thr[P]; matrix[Smax,Smax] y[P*P]; } transformed data{ matrix[Smax,Smax] x[P,P]; int i = 0; for(p1 in 1:P){ for(p2 in 1:P){ i = i + 1; x[p1,p2] = y[i]; } } } parameters{ cholesky_factor_corr[P] L_rho; } transformed parameters{ corr_matrix[P] rho = multiply_lower_tri_self_transpose(L_rho); } model{ for(p1 in 1:P){ for(p2 in (p1+1):P){ int S1 = S[p1]; int S2 = S[p2]; for(s1 in 1:S1){ for(s2 in 1:S2){ if(x[p1,p2][s1,s2]!=0){ target += x[p1,p2][s1,s2] * polychoric(thr[p1],thr[p2],s1,s2,rho[p1,p2]); } } } } } L_rho ~ lkj_corr_cholesky(1); } |
ポイントは,カテゴリ数が違う変数が入ってる場合にも対応するように,一番カテゴリ数が大きいものをSmaxという変数に入れて,それにあわせてベクトルの要素数などを定義しています。カテゴリ数が小さい変数の場合は適当な数字を入れておきます。実際には推定に使わないので数値であればなんでもいいです。
次に,相関行列を直接サンプリングするより,相関行列のコレスキー分解の要素を推定するほうが安定して,「正定値になってないよ!」,というエラーを防げます。初期値もピアソンの相関行列のコレスキー分解したものを入れます。
ほかにも多変量バージョンにするためにちょいちょい面倒なことやってますが,推定部分で言えばそんなに難しいことはしていません。
こちらも関数を用意しました。polycorr.stan2()です。好きなように名前は変えてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
polycorr.stan2 <- function(data,model,iter=4000,warmup=NULL,chains=4,cores=1){ if(is.null(warmup)) warmup = iter/2 P <- ncol(data) S <- c() for(i in 1:P) S[i] <- length(table(data[,i])) Smax <- max(S) thr <- list() af <- 5 for(p in 1:P){ temp <- qnorm(cumsum(table(data[,p])/length(data[,p])))[-S[p]] thr[[p]] <- c(-af,temp,af,rep(99,Smax-S[p]+1)) } y <- list() i <- 0 for(p1 in 1:P){ for(p2 in 1:P){ i <- i +1 x <- matrix(rep(99,Smax^2),nrow=Smax,ncol=Smax) x[1:S[p1],1:S[p2]] <- table(data[,p1],data[,p2]) y[[i]] <- x } } data.pm <- list(P=P,Smax=Smax,thr=thr,y=y) init.vb <- list(L_rho=t(chol(cor(data)))) init.pm <- list() for(c in 1:chains){ init.pm[[c]] <- init.vb } cat("MCMC sampling start.\n") fit.pm <- sampling(model,data=data.pm,init=init.pm,iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.pm) } |
次のコードで実行します。
|
1 2 3 4 5 6 |
dat <- na.omit(bfi[1:5]) model.pm <- stan_model("polychoric_multi.stan") fit2 <- polycorr.stan2(dat,model.pm,cores=1) print(fit2,pars="rho") |
推定には4000回で125秒程度でした。相関係数の数が10個なので,個別に推定したほうが早いという結果が・・・(笑)。
結果は以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
Inference for Stan model: polychoric_multi. 4 chains, each with iter=4000; warmup=2000; thin=1; post-warmup draws per chain=2000, total post-warmup draws=8000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat rho[1,1] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 8000 NaN rho[1,2] -0.41 0 0.02 -0.44 -0.42 -0.41 -0.40 -0.37 8000 1 rho[1,3] -0.33 0 0.02 -0.36 -0.34 -0.33 -0.31 -0.29 8000 1 rho[1,4] -0.18 0 0.02 -0.22 -0.19 -0.18 -0.16 -0.13 8000 1 rho[1,5] -0.23 0 0.02 -0.27 -0.24 -0.23 -0.21 -0.19 8000 1 rho[2,1] -0.41 0 0.02 -0.44 -0.42 -0.41 -0.40 -0.37 8000 1 rho[2,2] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 7824 1 rho[2,3] 0.56 0 0.01 0.53 0.55 0.56 0.57 0.58 8000 1 rho[2,4] 0.39 0 0.02 0.35 0.38 0.39 0.40 0.42 8000 1 rho[2,5] 0.45 0 0.02 0.41 0.44 0.45 0.46 0.48 8000 1 rho[3,1] -0.33 0 0.02 -0.36 -0.34 -0.33 -0.31 -0.29 8000 1 rho[3,2] 0.56 0 0.01 0.53 0.55 0.56 0.57 0.58 8000 1 rho[3,3] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 244 1 rho[3,4] 0.41 0 0.02 0.37 0.40 0.41 0.42 0.44 8000 1 rho[3,5] 0.57 0 0.01 0.55 0.56 0.57 0.58 0.60 8000 1 rho[4,1] -0.18 0 0.02 -0.22 -0.19 -0.18 -0.16 -0.13 8000 1 rho[4,2] 0.39 0 0.02 0.35 0.38 0.39 0.40 0.42 8000 1 rho[4,3] 0.41 0 0.02 0.37 0.40 0.41 0.42 0.44 8000 1 rho[4,4] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 6133 1 rho[4,5] 0.35 0 0.02 0.32 0.34 0.35 0.37 0.39 8000 1 rho[5,1] -0.23 0 0.02 -0.27 -0.24 -0.23 -0.21 -0.19 8000 1 rho[5,2] 0.45 0 0.02 0.41 0.44 0.45 0.46 0.48 8000 1 rho[5,3] 0.57 0 0.01 0.55 0.56 0.57 0.58 0.60 8000 1 rho[5,4] 0.35 0 0.02 0.32 0.34 0.35 0.37 0.39 8000 1 rho[5,5] 1.00 0 0.00 1.00 1.00 1.00 1.00 1.00 57 1 |
対角行列は推定対象じゃないので,rhatは気にしなくていいです。それ以外が収束しているのはわかると思います。
事後分布を見てみます。
|
1 |
fit2 %>% stan_dens(pars="rho",separate_chains = T) |
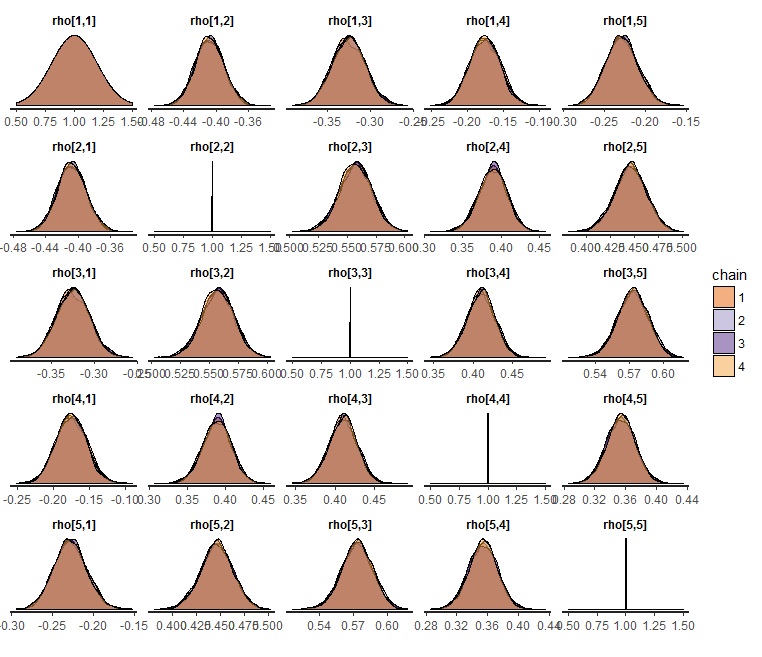
うまく収束しています。
次に,これを相関行列の形式で出力します。medianを使ってみました。
|
1 2 3 |
fit2 %>% rstan::extract() %$% rho %>% apply(c(2,3),median) %>% print(digits=2) |
|
1 2 3 4 5 6 |
[,1] [,2] [,3] [,4] [,5] [1,] 1.00 -0.41 -0.33 -0.18 -0.23 [2,] -0.41 1.00 0.56 0.39 0.45 [3,] -0.33 0.56 1.00 0.41 0.57 [4,] -0.18 0.39 0.41 1.00 0.35 [5,] -0.23 0.45 0.57 0.35 1.00 |
polychoric()の結果は以下です。最尤法の結果ときれいに一致しているのがわかると思います。
|
1 2 3 4 5 6 7 8 |
Call: polychoric(x = dat) Polychoric correlations A1 A2 A3 A4 A5 A1 1.00 A2 -0.41 1.00 A3 -0.33 0.56 1.00 A4 -0.18 0.39 0.41 1.00 A5 -0.23 0.45 0.57 0.35 1.00 |
これだけキレイに一致するんなら最尤法でいいじゃないか,という気もしますが・・・ データによっては最尤法は不適解(-1~1の範囲を超える)が出たり,標準誤差がめちゃくちゃ大きくなったり不安定な結果になることもあります。MCMCだとそのあたりは安定して推定できるので,最尤法だとうまくいかないときの選択肢としていいかなと思います。
明日のStan Advent Calendarも僕ですが,今回のポリコリック相関行列を使ってカテゴリカル因子分析を実行する方法について書く予定です。
Enjoy!
関数をまとめたコード
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
library(rstan) library(psych) library(dplyr) polycorr.stan <- function(data,model,iter=4000,warmup=2000,chains=4,cores=1){ S1 = nrow(table(data)) S2 = ncol(table(data)) absinf <- 5 thr1 = qnorm(cumsum(table(data[,1])/length(data[,1])))[-S1] thr2 = qnorm(cumsum(table(data[,2])/length(data[,2])))[-S2] data.poly <- list(S1=S1,S2=S2,absinf=absinf,y=table(data)) init.vb <- list(a=thr1,b=thr2,rho=cor(data)[1,2]) init.poly <- list() for(c in 1:chains) init.poly[[c]] <- init.vb cat("MCMC sampling start.\n") fit.poly <- sampling(model,data=data.poly,init=init.poly, iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.poly) } polycorr.stan1 <- function(data,model,iter=4000,warmup=2000,chains=4,cores=1){ S1 = nrow(table(data)) S2 = ncol(table(data)) absinf <- 5 thr1 = c(-absinf,qnorm(cumsum(table(data[,1])/length(data[,1])))[-S1],absinf) thr2 = c(-absinf,qnorm(cumsum(table(data[,2])/length(data[,2])))[-S2],absinf) data.poly <- list(S1=S1,S2=S2,a=thr1,b=thr2,absinf=absinf,y=table(data)) init.vb <- list(rho=cor(data)[1,2]) init.poly <- list() for(c in 1:chains) init.poly[[c]] <- init.vb cat("MCMC sampling start.\n") fit.poly <- sampling(model,data=data.poly,init=init.poly, iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.poly) } polycorr.stan2 <- function(data,model,iter=4000,warmup=2000,chains=4,cores=1){ P <- ncol(data) S <- c() for(i in 1:P) S[i] <- length(table(data[,i])) Smax <- max(S) thr <- list() af <- 5 for(p in 1:P){ temp <- qnorm(cumsum(table(data[,p])/length(data[,p])))[-S[p]] thr[[p]] <- c(-af,temp,af,rep(99,Smax-S[p]+1)) } y <- list() i <- 0 for(p1 in 1:P){ for(p2 in 1:P){ i <- i +1 x <- matrix(rep(99,Smax^2),nrow=Smax,ncol=Smax) x[1:S[p1],1:S[p2]] <- table(data[,p1],data[,p2]) y[[i]] <- x } } data.pm <- list(P=P,Smax=Smax,thr=thr,y=y) init.vb <- list(L_rho=t(chol(cor(data)))) init.pm <- list() for(c in 1:chains){ init.pm[[c]] <- init.vb } cat("MCMC sampling start.\n") fit.pm <- sampling(model,data=data.pm,init=init.pm,iter=iter,warmup=warmup,chains=chains,cores=cores) return(fit.pm) } |