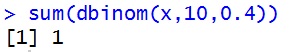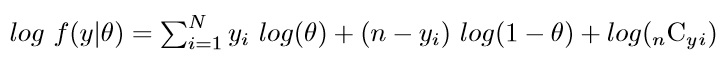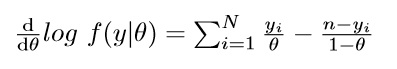最近はstanでMCMCするのが楽しいわけですが,僕のごくごく近い範囲の人間から「そもそも尤度ってなんだ」という話があったので,今回は尤度や最尤推定法について書きます。
統計モデリングは確率分布を扱う
何を今更,と思うかもしれませんが,統計モデリングと確率分布は切っても切れない関係にあります。今回は二項分布について話をします。次回はたぶん正規分布について書きます。
さて,二項分布とは,成功と失敗といった2値で表現される結果がでる試行をN回繰り返したとき,成功する回数について表される確率分布です。詳しくはWikipediaを見てください。
二項分布は試行回数と成功確率が決まれば分布の形が決まります。ここで,Rを使って分布を直感的に理解してみましょう。
ここでは試行回数は10回で,成功率は0.5としましょう。バスケットボールのシュートが入るかどうかとか,バッティング練習でヒットになるかどうかとか,具体的にイメージするといいでしょう。
二項分布に従う確率は,Rのdbinom()で簡単に計算できます。Rには様々な確率分布の関数があるのでとても便利です。二項分布はbinomにdをつければ確率密度関数,rをつければ二項乱数を発生される関数,pをつければ累積確率,qをつければパーセンタイル点を返す関数になります。詳しくは「R 確率分布」でググってください。
さて,dbinom()は最初に成功回数,次に試行数,最後に成功率を入力します。0.5の成功率で10回試行して,仮に3回成功する確率を知りたいとすると,以下のように書きます。
|
1 |
dbinom(3,10,0.5) |
成功率は0.117,つまり約12%です。続いて,5回成功する確率は,
|
1 |
dbinom(5,10,0.5) |
となります。
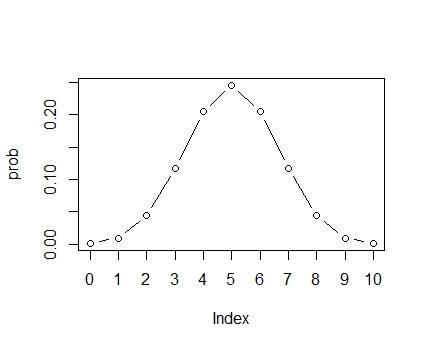
次に,成功する回数を0~10回を順番にいれて分布の形を見るには次のように書きます。
|
1 2 3 4 |
x <- rep(0:10) prob <- dbinom(x,10,0.5) plot(prob,type="b",xaxt="n") axis(side=1,at=1:11,labels=x) |
このように,5回が最も確率が高くなるような分布になります。
さて,確率分布は定義上,全部足せば1になります。それを確認してみましょう。
まず以下のコードを書いて,10試行中,0回,1回,2回3回・・・とそれぞれの成功数のときの確率を計算してみましょう。
|
1 2 |
x <- rep(0:10) dbinom(x,10,0.4) |
このように11個の確率が計算されました。
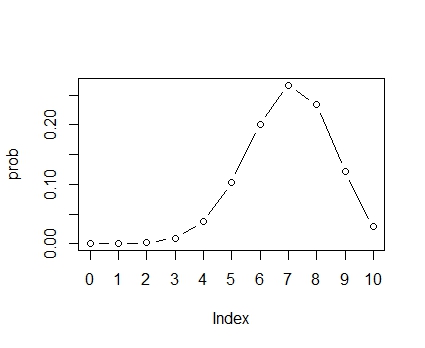
これを合計してみます。
|
1 |
sum(dbinom(x,10,0.4)) |
このように,総和は1になります。
統計モデリングは確率分布のパラメータを推定する
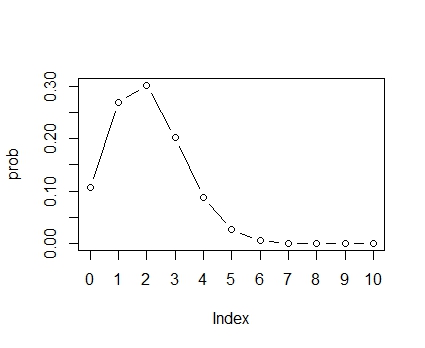
さて,統計モデリングが確率分布のパラメータを推測する,というのはどういうことでしょうか。確率分布のパラメータとは,分布の形を決める数値のことで,分布によって色んな種類があります。二項分布のパラメータは試行数を固定すれば,成功率がパラメータとなります。成功率が0.2の場合,0.7の場合についてそれぞれ分布の形を見てみましょう。
|
1 2 3 |
prob <- dbinom(x,10,0.2) plot(prob,type="b",xaxt="n") axis(side=1,at=1:11,labels=x) |
|
1 2 3 |
prob <- dbinom(x,10,0.7) plot(prob,type="b",xaxt="n") axis(side=1,at=1:11,labels=x) |
このように,パラメータである成功率を変えると,分布の形が変わるのです。
よく使われる正規分布は,平均値と分散という2つのパラメータがあります。大抵の分布は分布の位置を表す位置パラメータ(平均値みたいなやつ)と,分布の散らばりの程度を表す尺度パラメータ(分散みたいなやつ)の2つがあります。ただ,二項分布やポアソン分布のように離散分布にはパラメータが1つしかないものもあります(厳密いえば二項分布は成功率以外に試行数も分布の特徴を決めるパラメータといえる)。
統計モデリングは,得られたデータの分布に近くなるように,確率分布のパラメータを推定します。そうすることで,少ない量のパラメータで多くのデータを表現することができるようになります。
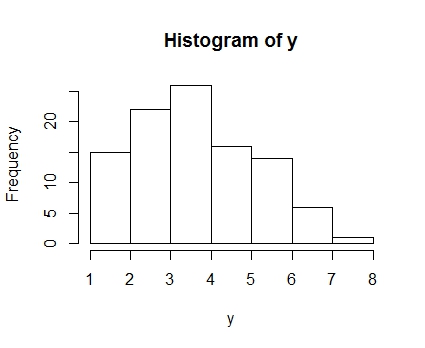
たとえば,真の分布が成功率0.4の試行数10の二項分布からデータが100人分得られたとします。そのデータの分布は次のようになりました。二項分布から乱数を発生させるのはrbinom()を使います。最初に発生させたいデータ数,次に試行数,最後に成功率を入れます。
|
1 2 3 |
set.seed(5) y <- rbinom(100,10,0.4) hist(y) |
※乱数の種(seed)をコードにあるように,5に固定すれば,全く同じデータが得られます
実際は真の分布が何かわかりません。そこで二項分布だと仮定した上で,そのパラメータである成功率がどの程度なのかを手元にあるデータから推定します。それが我々が普段やっている,統計分析です。上にあげたように,0.2や0.7の成功率をパラメータとしていれた二項分布は,このデータのヒストグラムとは一致してなさそうなのがわかると思います。
心理系の人なら回帰分析をよく使いますが,回帰分析はデータが正規分布から発生していると仮定した上で,正規分布のパラメータである平均値と分散を推定します。平均値は説明変数によって変動すると考えると,正規分布の分散パラメータは説明変数による個人差の変動分だけ,データの分散よりは小さく推定されます。これが残差分散と呼ばれるものです。回帰分析についてはまた改めて記事を書こうと思います。
さてさて,ではどうやって確率分布のパラメータを推定するのでしょうか。そこで登場するのが尤度というものです。
尤度ってなんだろう
尤度とは,確率とそっくりです。しかし,考え方が違います。
確率は,あるパラメータの分布から特定のデータがどれほど得られやすいかを表したものでした。一方,尤度とは,あるデータを得たときに,分布のパラメータが特定の値であることがどれほどありえそうか(尤もらしいか)を表したものです。確率はパラメータを固定してデータが変化しますが,尤度はデータを固定してパラメータが変化するのです。
例えば,10回やって3回成功したというデータがあったとしましょう。その場合,そのようなデータが得られたときに二項分布の成功率が0.4であるのがどれほどありえそうか(尤もらしいか)を考えます。いうなれば,10回中3回成功したことがわかっているときの,成功率が0.4である条件付き確率を考えるのです。
実は,これも先程と同様dbinom()で計算することができます。つまり,
|
1 |
dbinom(3,10,0.4) |
のようになります。
でもあれ?このコード,さっき確率を計算した時と同じような・・・ 尤度と確率って同じ・・・? あるデータが得られたときの特定のパラメータの尤度は,データが得られたときの条件付き確率なので,基本的には確率と同じ関数で数値を得ることができるのです。
でも,尤度と確率は「分布を考えたとき」には別物です。それは,関数の中で変化する値が違うからです。
確率は成功率を固定した状態で,成功数がいろいろ変化していました。その結果,すべての成功数における確率を足すと1になりました。
一方,尤度は「成功数を固定して,成功率が変化する」ということを考えるのです。成功率は0~1の範囲をとるので,連続的に数値を入れてみます。ここで,二項分布の尤度を計算するための新しい関数を作ってみましょう。名前はbinom_lik()とします。
|
1 2 3 |
binom_lik <- function(z){ dbinom(3,10,z) } |
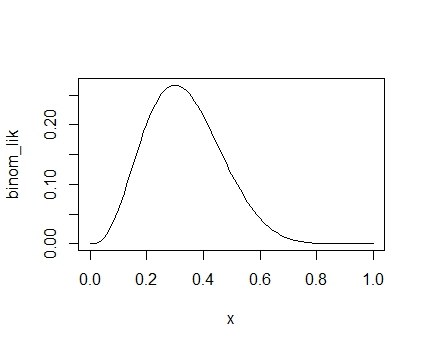
これを使って,パラメータを0~1の間でつぎつぎに変化させて入力した場合の尤度をプロットしてみると次のようになります。plot()にベクトルを引数に入れられる関数をいれると,分布を表示してくれるのです。便利。
|
1 |
plot(binom_lik,xlim=c(0,1)) |
このように,0.3あたりで最も高くなるような連続型の分布になります。これが尤度の分布です。見てわかるように,二項分布の確率分布とは別物です。
尤度と確率の大きな違いは,尤度は総和が1にならないということです。上で見たように,確率は総和が1になります。連続分布の場合は総和が計算出来ないので,代わりに積分を使います。Rのintegrate()で0から1までの成功率の尤度の積分を計算してみると,
|
1 |
integrate(binom_lik,0,1) |
というように,1になりませんでした。
念のため,連続分布である正規分布の確率密度関数の積分をとってみましょう。
このように,確率分布であれば積分すると1になります。
※integrateは最初の引数である,実現値を変化させた場合の関数の積分をとります。なので,ここでは確率分布としてあつかわれていることになるのです
まとめると,尤度はあるデータを得たとき,真の分布のパラメータが特定の値であることの尤もらしさを表しています。なので確率と意味的にはかなり近いものです。実際,データを得たときのパラメータについての条件付き確率として計算できます。でも分布に注目すると,数学的な定義として積分した値が1にならないので「確率」ではなく「尤度」という別の言葉を当てているのです。
最尤法は尤度を最大にするパラメータを決める方法のこと
尤度は,データ(今回の場合は成功数)を固定して,パラメータを変化させたときの分布でした。
先ほど見たように,10回中3回成功したというデータは,パラメータが0.3の時に最も尤度が高くなりました。これは,「10回中3回成功するというデータが発生するのは,二項分布の成功率が0.3の時に最も起こりやすい」ということを意味しています。
さてここまで書けばわかると思いますが,最尤法とは,尤度が最も高くなるような値をパラメータの推定値として使おう,という推定方法です。尤度が最大のパラメータを推定する方法だから,最尤法,というわけです。
我々が算数で習った,試行数で成功回数を割ると成功率が出る,という計算方法は,実は最尤推定量でもあるのです。なので二項分布の成功率パラメータを推定するのに,別に難しい計算なんかせずとも3/10で0.3と簡単に求まります。しかし,そもそもなぜその計算でできるのか,を考えてみましょう。
※推定量と推定値の違い,わかりにくいですね。推定値は実際に推定されたパラメータの値です。一方,推定量とはパラメータを推定する計算式というか,手続きのことを指します。尤度を最大にするという理屈で求められたパラメータを計算するための式が最尤推定量,それによって実際に計算された値が最尤推定値,ということです。
では,先ほど乱数で発生させた真の成功率0.4の100人のデータから,最尤法を使ってパラメータを推定してみましょう。もう一度ヒストグラムを載せておきます。
先ほどまでは1つの実現値(10回やって3回成功した)の尤度を計算していましたが,100人分のデータを同時に分析するとなると,尤度はどのようになるのでしょうか。100人分のデータを分析するとは,100人がそれぞれ別々に10回試行して,それぞれ何回成功したかについてのデータを使って,全体的な成功率を推定する,ということです。もちろんここでは,個人差は無視しています。みんなが同じ成功率であると仮定しての話です。
尤度は確率と同じように,試行がそれぞれ独立であれば,その積で同時分布を計算することができます。試行が独立であるとは,それぞれの人が他の人とは全く関係なくシュートなりバッティングをしたということです。大抵のサンプリング理論で仮定されているものです。
では,発生させた二項乱数yについて,尤度を計算します。要素の積を返す関数にprod()がありますので,それを使います。なお,試行数は10で固定しています。
まず,パラメータが0.4のとき,yというデータが得られた時の尤度は次のコードで計算できます。
|
1 |
prod(dbinom(y,10,0.4)) |
ちっさ!
小数点のあと0が80個以上続くほど小さい値です。
というわけで,一人ひとりの尤度を全部かけると,どんどん小さい値になっていきます。100人分もかけるととても小さい値になります。
尤度の同時分布(100人分の尤度の積の分布)は,次のコードで書けます。ただ,plotさせるためにベクトルに対応した関数の作り方にしています。関数の中にもう一つtempという関数をかましていますが,これはsapplyに入れるためのダミーの関数です。関数の肝はprod(dbinom(y, 10, x))のところです。
|
1 2 3 4 5 |
binom_lik2 <- function(x){ temp <- function(x) prod(dbinom(y,10,x)) return(sapply(x,temp)) } plot(binom_lik2,xlim=c(0,1)) |
なんか分布が細くなりましたね。
これは,データ数が増えることで真のパラメータがこの辺りにあるということについての精度が高くなっている,ということです。真値は0.4ですが,0.4よりやや高めのところが最尤推定値になっているのがわかります。
なお,100人分のデータであっても,解析的に最尤推定値は計算できます。yの平均値を試行数の10で割ればいいだけです。これを計算すると,0.41になります。
|
1 |
mean(y/10) |
尤度を最大化してパラメータを推定する
さて,尤度の同時分布まで計算できたわけですが,ここから尤度が最大になるパラメータが何かを知る必要があります。これを知るには,尤度関数を微分して,極値を求めてやればいいのです。高校で習ったアレです。
でも,尤度は積で構成されているので,実はとても微分がやりづらい。そこで,対数をとります。対数をとっても大小関係は変わらないので,最大化することによって得られる推定値はおなじになります。また,対数をとると,積から和に変わるので計算が楽ちんになるのです。あと,値も小さくなくなってわかりやすい。
この対数をとった尤度関数を「対数尤度関数」と呼びます。二項分布の対数尤度関数は,次のようになります。
なお,データがy,データ数がN,試行数がn,成功確率がθです。
対数尤度関数は,Rだとただ単にdbinom()にlogをつけて合計すればいいだけなので簡単です。
|
1 2 3 4 5 |
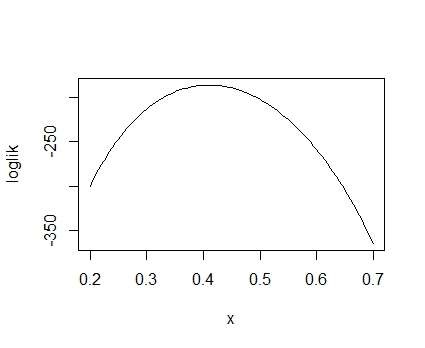
loglik <- function(x){ temp <- function(x) sum(log(dbinom(y,10,x))) return(sapply(x,temp)) } plot(loglik,xlim=c(0.2,0.7)) |
1より小さい値の対数は負になるので,大抵対数尤度は負になります(正になることもまれにあります)。グラフを見てわかるように,やはり0.4付近の対数尤度が最大になっています。
この対数尤度関数の最大値,つまり極値を知るためには,微分して接線の傾きが0となるパラメータを知ればいいわけです。というわけで微分してみましょう。対数尤度関数の導関数は次のようになります。
なお,コンビネーションがあるところはパラメータθに関係ないところなので,微分すると消えます。
この一次導関数を関数化してみましょう。今回もベクトルを引数にしたいので,次のように書きました。なお,関数中にある10-yの10とは,試行数の10です。
|
1 2 3 4 5 6 7 |
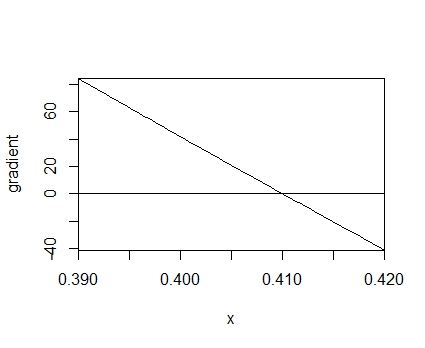
gradient <- function(theta){ temp <- function(theta) sum(y/theta-(10-y)/(1-theta)) return(sapply(theta,temp)) } plot(gradient,xlim=c(0.39,0.42)) abline(h=0) |
だいたい,0.41ぐらいで対数尤度の導関数が0になっているのがわかると思います。
さて,二項分布のように簡単な確率分布の場合,この一次導関数を展開すれば,さきほどのようにパラメータθは解析的に求めることができます。それが,yの平均値を試行数で割る,というものです。算数で習ったあの式は,厳密にはこのプロセスを経て得られるわけです。
長くなったので,今回はここまでにしておきます。次の記事では,最尤法をニュートン法で解く,というのを扱ってみたいと思います。