前回の記事の続きになるので,未読の人は先にこちらの記事を読んでください。
さて,前回は尤度と最尤法について書きました。
前の記事のおさらい
尤度が最大になるようなパラメータを推定値とするのが最尤推定法でした。具体的には,尤度関数の対数をとった対数尤度関数を微分して,導関数が0となるような推定値が,最尤推定値となる,ということでした。
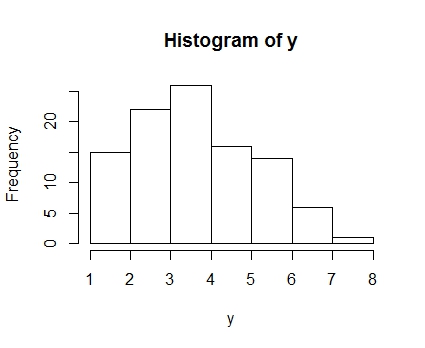
前の記事で使ったデータは,10回の試行で成功率0.4の二項分布に従う乱数でした。次のコードで同じデータが生成できます。
|
1 2 3 |
set.seed(5) y <- rbinom(100,10,0.4) hist(y) |
このデータから,逆にもともと設定した成功率のパラメータがなんだったかを推定しよう,というわけです。
なお,このデータの最尤推定値は,yの平均を試行数の10で割ったもの,つまり
|
1 |
mean(y/10) |
と,0.41であることがわかります。
このように,二項分布のような簡単な分布の場合,導関数を解析的に解けばパラメータを計算できる式を直接得ることができます。しかし,一般的な統計モデリングでは推定するべきパラメータが複数になり,分布の式ももっと複雑なので,簡単には解けません。
そこで,使うのが非線形方程式を解く方法です。手法はいろいろあって,ニュートン-ラフソン法(単にニュートン法ともよぶ),準ニュートン法,EMアルゴリズム,などなどです。今回は,一番わかり易いニュートン法で解いてみましょう。
ニュートン法の手続き
ニュートン法は,詳しくはWikipediaを見てもらったらいいのですが,簡単にいえば一次導関数と二次導関数を使って,ちょっとずつパラメータを変えながら正解にたどり着く方法です。
ニュートン法の手順は,
- まず適当な(それなりに正解に近い)初期値を決める。
- 一次導関数,二次導関数に初期値を入れて,それぞれの値を得る
- 一次導関数の値を二次導関数の値で割った値に負数をかけたものを変化量とする
- 初期値に変化量を加えて,変化量が十分小さくなるまで繰り返す
というものです。
なんでこの手続で解が求まるのかについてはこの際おいておいて,手続き的には上の方法で非線形方程式の解がもとまってしまうのです。
しかし,この手続を実行するためには二次導関数が必要になります。僕みたいに数学がちゃんとできない人間は微分とかよくわからないので(おい),ここでは簡単に二次導関数を計算する方法を紹介します。それはズバリ,数値微分です。邪道です。
数値微分は,微小値を動かして,その変化量を使って微分する,という方法です。前の記事で書いた一次導関数を求めるgradient()を使えば,簡単に計算できます。
|
1 2 3 4 5 6 7 8 9 |
#試行数10の二項分布の成功率についての尤度関数の導関数 gradient <- function(theta){ temp <- function(theta) sum(y/theta-(10-y)/(1-theta)) return(sapply(theta,temp)) } h <- 0.001 #微小値 first <- gradient(theta) #一次導関数 second <- (gradient(theta+h)-first)/h #二次導関数 |
このように,微小値hを推定値に足した場合の値から一次導関数の値を引いて,微小値で割ると近似的に二次導関数の値を得ることができます。
これを利用して,ニュートン法を実行してみましょう。変化量は,一次導関数の値を二次同感数の値で割ってやったものに-1をかけたものです。それがchangeという変数に入っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#試行数10の二項分布の成功率についての尤度関数の導関数 gradient <- function(theta){ temp <- function(theta) sum(y/theta-(10-y)/(1-theta)) return(sapply(theta,temp)) } theta <- 0.3 #成功率の初期値として0.3を入れる h <- 0.001 #微小値 #ニュートン法開始 first <- gradient(theta) #一次導関数 second <- (gradient(theta+h)-first)/h #二次導関数 change <- -1 * first / second change #変化量 theta <- theta + change theta #新しい推定値 |
となり,0.3に変化量の0.09を足して,新しい推定値である0.39を得ました。この時点で正解の0.41に近い値が出ているのがわかります。
もう一回同じコードを走らせてみると・・・
|
1 2 3 4 5 6 7 |
#新しいthetaを使って,もう一度導関数を計算して,変化量を計算 first <- gradient(theta) #一次導関数 second <- (gradient(theta+h)-first)/h #二次導関数 change <- -1* first / second change #変化量 theta <- theta + change theta #新しい推定値 |
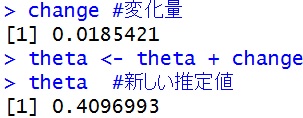
今度は0.409とさらに正解に近い値まで来ました。たった2回でこんなにも近くなるのがニュートン法のすごいところです。なお,もう一度やると,
変化量も0.0003とかなり小さくなり,ほぼ正解になりました。
ただ,毎回コードを走らせてても面倒なので,この手続を繰り返し処理に任せることにしましょう。すると,次のようなコードになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
theta <- 0.3 #成功率の初期値として0.3を入れる h <- 0.001 #微小値 ep <- 1 #収束を判断する指標 i <- 0 #繰り返し回数を数える #ニュートン法開始 while(ep>0.0001){ first <- gradient(theta) #一次導関数 second <- (gradient(theta+h)-first)/h #二次導関数 change <- -1 * first / second theta <- theta + change ep <- abs(change) i <- i + 1 } theta |
試しに初期値を0~1の範囲で変えてみましょう。たいていの数値なら正解の0.41にたどり着くはずです。しかも,だいたい5~6回で収束します。
ロジット変換で推定する
さて,これで無事にニュートン法で最尤推定ができました。
次に,もう少しマニアックな話を。
今回,成功率パラメータは0~1の範囲を取るものでしたが,このように定義域が決まっているパラメータは推定のときにいろいろ面倒です。なぜなら,定義域を超えると関数自体が正常な値を返してくれなくなるからです。
そこで,変数を変換して上限と下限をなくしたうえで推定できると便利です。
確率である成功率は,ロジット変換をしてやると上限と下限がそれぞれ無限大になるので,推定がやりやすくなります。
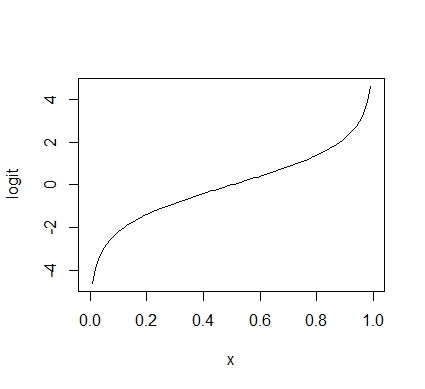
ロジット変換とは,0~1の範囲をとる値を,上限・下限がない値に変換します。logit()に値をいれると変換してくれます。試しにplotしてみると,次のようになります。
|
1 |
plot(logit) |
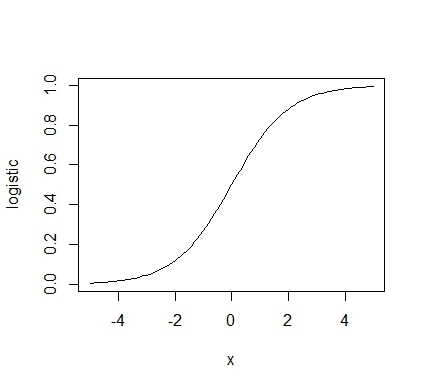
また,logit()の逆関数はlogistic()というのがあります。これはロジット得点をいれると0~1の範囲の数値に変換します。これをロジスティック変換といいます。
|
1 |
plot(logistic,xlim=c(-5,5)) |
それでは,ロジット変換を使って最尤推定してみましょう。まず対数尤度関数を作ってみましょう。何も難しいことはなくて,引数がロジット得点であることを想定して,中でロジスティック変換させればいいだけです。なお,関数の中の10は,試行数が10回であることを意味しています。
|
1 2 3 4 5 6 |
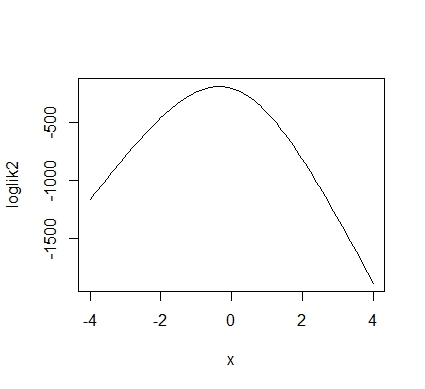
loglik2 <- function(x){ temp <- function(x) sum(log(dbinom(y,10,logistic(x)))) return(sapply(x,temp)) } plot(loglik2,xlim=c(-4,4)) |
さて,対数尤度が最大になるのは-0.3ぐらいでしょうか。
では,さっきのニュートン法を使って推定してみましょう。コードは,gradient()の中身にlogistic変換を入れた新しい関数を作って,それでグルグル回します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#試行数10の二項分布のロジット変換した成功率についての尤度関数の導関数 gradient2 <- function(x){ h <- 0.001 temp <- function(x) sum(y/logistic(x)-(10-y)/(1-logistic(x))) #ロジスティック変換を施す return(sapply(x,temp)) } logit_theta <- logit(0.3) #成功率の初期値として0.3を入れる h <- 0.001 #微小値 ep <- 1 #収束を判断する指標 i <- 0 #繰り返し回数を数える #ニュートン法開始 while(ep>0.00001){ first <- gradient2(logit_theta) #一次導関数 second <- (gradient2(logit_theta+h)-first)/h #二次導関数 change <- -1 * first / second logit_theta <- logit_theta + change ep <- abs(change) i <- i + 1 } logit_theta logistic(logit_theta) i |
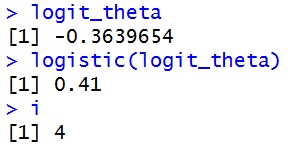
このように,ロジット変換をしたものでも4回の計算で収束しました。成功率のロジット得点の最尤推定値は-0.36で,それをロジスティック変換すると0.41という成功率の最尤推定値になります。
Rのoptim()で推定してみる
Rには,optim()という最適化のための関数があります。これは対数尤度関数を入れれば,後は勝手に最適化してくれて,解を出してくれるすぐれものです。便利!
optimは,上限と下限があるような関数だと上手く推定してくれないことが多いので,上でやったようにロジット変換をした対数尤度関数である,loglik2()を入れてみます。
次のように書きます。まず,最初に初期値をいれます。次に,最適化したい関数を入れます。control = list(fnscale=-1)は,もともと最小化のための関数であるoptimに最大化させたい場合に書きます。methodはいろいろありますが,いわゆる準ニュートン法と呼ばれるBFGSを入れています。
|
1 2 |
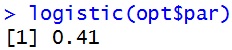
opt <- optim(0.3,loglik2,control=list(fnscale=-1),method="BFGS") logistic(opt$par) |
あっという間に解が求まります。
Rのglm()で解いてみる
Rにはglmという一般化線形モデル用の関数がありますから,これを使っても簡単に解けます。二項分布を仮定した回帰分析をする場合,目的変数をcbind(成功数,失敗数)というように書きます。失敗数は試行数から成功数を引けばいいので,cbind(y,10-y)とすればいいことになります。
|
1 2 3 4 |
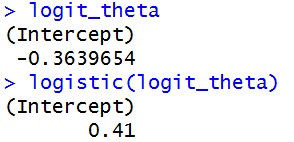
result <- glm(cbind(y,10-y)~1,family=binomial) #二項分布回帰分析 logit_theta <- result$coefficients #推定値を取り出す logit_theta logistic(logit_theta) |
このように,同じ解が得られます。