Stanで媒介分析 | Sunny side up!

先日，Stanの初心者講習の資料をアップしました。思った以上に反響があって驚いています。

さて，知り合いから媒介分析をStanでやるには？という質問があったので，コードを書いておきます。レベル的には初心者レベル＋αぐらいでかけますので，そんなに難しくはありません。

ただ，媒介分析そのものを理解していないといけません。媒介分析そのものについては，僕が社会心理学会で発表したこちらの資料が役立つかと思います。媒介分析って何？というかたはこちらを先にご覧ください。

媒介分析は，ブートストラップ法やらソベルテストやらいろんな検定法があり，ブートストラップ法にもバイアス修正とか，ノンパラやらパラメトリックやらいろいろ手法があり理解するのが大変です。

それに対して，MCMCによるベイズ推定だと，間接効果の推定はごく自然に行うことができます。つまり，パスの積の信用区間をそのまま，パスの積を計算するだけでOKだからです。そこに手法の多様性なんかはありません。事後分布が手に入るだけです。

というわけで，MCMCを使う一つのモチベーションのいい例かなと思ったので記事にしてみました。

データ

今回使うのは，2014年のプロ野球の野手199名のデータです。プロ野球データフリークからダウンロードしました。ここから，選手の体重，年俸，ホームランの本数，というデータを使います。ただし，年俸は対数正規分布に従うのでここでは処理を簡単にするため対数変換しています。

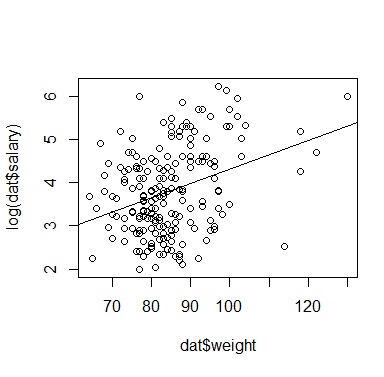
まず，体重と対数年俸の相関を見てみます。

plot(dat$weight,log(dat$salary))
abline(lm(log(salary)~weight,dat))

1 2	plot(dat$weight,log(dat$salary)) abline(lm(log(salary)~weight,dat))

相関係数は，0.334，95%CIは.204～.452でした。

なんと，体重が重いほうが年俸が高くなる！太れ野球選手！

というわけはなく，これがHRの本数で媒介されるというモデルを考えます。つまり，体重が重く筋力がある選手ほどHRをよく打ち，その結果年俸が増える，というわけです。重いだけでは給料が増えない，ということが示したいです。

某統計ソフトで分析した結果が以下です。係数は標準化しています。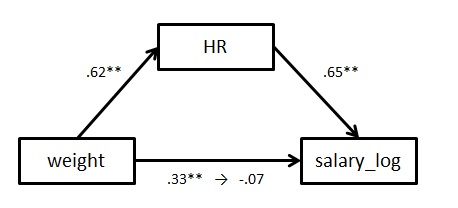

体重と対数年俸の関係は，ホームランを媒介変数として投入することで完全に消えています。つまり，体重と年俸の関係は「ホームランを打つかどうか」で説明できたわけです。

なお，標準化間接効果は.401で有意でした。

これをStanで実装してみましょう。

Stanコード

Stanコードは以下になります。

data{
  int N; //sample size
  vector[N] y; //dv
  vector[N] x; //iv
  vector[N] m; //mediation variable
}
parameters{
  real intcpt_y;
  real intcpt_m;
  real a;
  real b;
  real c;
  real<lower=0> sigma_y;
  real<lower=0> sigma_m;
}
model{
  //prior
  intcpt_y ~ normal(0,100);
  intcpt_m ~ normal(0,100);
  a ~ normal(0,100);
  b ~ normal(0,100);
  c ~ normal(0,100);
  sigma_y ~ cauchy(0,5);
  sigma_m ~ cauchy(0,5);
  //regression model
  y ~ normal(intcpt_y+c*x+b*m,sigma_y);
  m ~ normal(intcpt_m+a*x,sigma_m);
}
generated quantities{
  //indirect effect
  real indirect;
  indirect <- a*b;
}

data{

int N; //sample size

vector[N] y; //dv

vector[N] x; //iv

vector[N] m; //mediation variable

}

parameters{

real intcpt_y;

real intcpt_m;

real a;

real b;

real c;

real sigma_y;

real sigma_m;

}

model{

//prior

intcpt_y ~ normal(0,100);

intcpt_m ~ normal(0,100);

a ~ normal(0,100);

b ~ normal(0,100);

c ~ normal(0,100);

sigma_y ~ cauchy(0,5);

sigma_m ~ cauchy(0,5);

//regression model

y ~ normal(intcpt_y+c*x+b*m,sigma_y);

m ~ normal(intcpt_m+a*x,sigma_m);

}

generated quantities{

//indirect effect

real indirect;

indirect <- a*b;

}

Stanでは年俸へのモデルと媒介変数HRへのモデルを同時に推定しています。そして，体重→HRのパスaと，HR→年俸へのパスbの積を間接効果として推定しています。単純に掛け算をしているだけですが，MCMCだとこれだけで間接効果の信用区間も計算できてしまいます。

Rコードは以下です。今回は係数を標準化したかったので，データを最初から標準化してからStanに入れています。

model1 <- stan_model("mediation1.stan")
x <- as.vector(scale(dat$weight))
y <- as.vector(scale(log(dat$salary)))
m <- as.vector(scale(dat$HR))
data <- list(N=199,x=x,y=y,m=m)
fit1 <- sampling(model1,data=data,iter=4000,warmup=1000)
print(fit1,probs=c(0.025,0.5,0.975),digits=3)

model1 <- stan_model("mediation1.stan")

x <- as.vector(scale(dat$weight))

y <- as.vector(scale(log(dat$salary)))

m <- as.vector(scale(dat$HR))

data <- list(N=199,x=x,y=y,m=m)

fit1 <- sampling(model1,data=data,iter=4000,warmup=1000)

print(fit1,probs=c(0.025,0.5,0.975),digits=3)

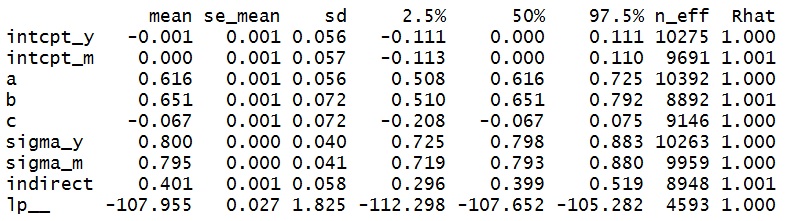
これを走らせると，以下の結果が得られます。

パスaが体重からHRの回帰係数，パスbがHRから対数年俸への係数です。

間接効果indirectはこの積で，.401[.296~.519]でした。それに対してHRを投入後の体重の効果はパスcで，-.067[-.208~.075]となりました。

つまり，標準化間接効果は大きな効果を持つ一方，直接効果はほぼ完全になくなりました。いわゆる完全媒介が成立したといえます。

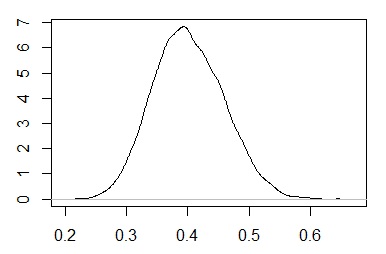
間接効果の事後分布も簡単に見れます。

indirect <- rstan::extract(fit1)$indirect
plot(density(indirect))

1 2	indirect <- rstan::extract(fit1)$indirect plot(density(indirect))

199人いると，かなり正規分布に近いですが，若干0の方向にゆがんでるのがわかるかと思います。

このようにStanというかMCMCを使うと媒介分析とその間接効果もごく自然に推定することができます。ブートストラップ法でもいいんですが，バイアス修正法とかいろいろややこしいことを考えずに済むのがMCMCによるベイズ推定のいいところですね。

なお，HRは正規分布じゃないので，そこをnormalではなく負の二項分布であるneg_binomial_log()に変えるとよりよいモデルになると思います。ただしその場合は，HRは標準化できないので注意が必要です。