この記事は、Stan Advent Calendar 2018の14日目の記事です。
今日は自動微分について書きます。とはいえ、僕も全然理屈わかってなくて「へーそうなんだー」ぐらいの感じです。
先日、同じくStanのアドカレ7日目で、俺式NUTS(別称:どんぐり)のコードを公開しました。RでもNUTSを使って推定できることがわかったわけですが、ちょいちょいごまかしているところがあります。
本来は対数尤度の勾配を計算するところで、自動微分というアルゴリズムを使うところなのですが、「どんぐり」では数値微分という方法を用いています。これらの違いについて説明した上で、自動微分をRで実行するためのパッケージ、madnessの紹介をしよう、というのが今回の記事に主旨です。
◆数値微分
数値微分は、パラメータを微小値を動かした場合に対数尤度の変化量を数値的に計算する方法です。
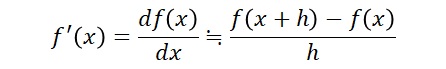
ここでhは0.001のような微小値をいれて計算します。どんぐりでは、次のような感じでパラメータ全部についての偏微分をRで計算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
grad_U <- function(U,theta,X,Y){ P <- length(theta) h <- 0.001 f <- U(theta,X,Y) dtheta <- c() for(i in 1:P){ theta_h <- theta theta_h[i] <- theta[i]+h dtheta[i] <- (U(theta_h,X,Y)-f)/h } return(dtheta) } |
Uは対数尤度を計算する関数で、引数になっています。数値微分は関数を引数にしてしまえば、それがどんな確率モデルであっても計算することができるので汎用性という意味ではとても便利です。
たとえば、ロジスティック回帰分析の確率モデルの対数尤度関数を考えてみます。
まずロジスティック関数を定義しておきます。あと、パイプ演算子をあとで使ってるのでここでmagrittr呼び出しておきます。
|
1 2 3 4 5 |
library(magrittr) inv_logit <- function(x){ 1/(1+exp(-x)) } |
これを用いて次のように確率モデルを定義します。
|
1 2 3 4 5 |
log_logistic <- function(theta,X,Y){ mu <- inv_logit(X%*%theta) LL <- sum(Y*log(mu)+(1-Y)*log(1-mu)) return(LL) } |
ロジスティック回帰は、ベルヌーイ分布のパラメータをロジットリンクにいれて線形モデルで予測するモデルです。それが表現されているのがわかるかと思います。LLは対数尤度をいれています。
たとえば、200人のサンプルデータを作ってみます。
|
1 2 3 4 5 6 7 8 |
##logistic beta <- rnorm(2,0,1) P <- length(beta) N <- 200 X <- MASS::mvrnorm(N,rep(0,P-1),diag(rep(1,P-1))) X <- as.matrix(cbind(rep(1,N),X)) mu <- inv_logit(X%*%beta) Y <- rbinom(N,1,mu) |
この場合の、真値(ここではbeta、回帰係数)を入れた場合の対数尤度の勾配を、数値微分で計算してみましょう。
|
1 |
grad_U(log_logistic,beta,X,Y) |
するとこのようになります。
|
1 2 |
> grad_U(log_logistic,beta,X,Y) [1] -2.880001 -6.885068 |
最尤推定量をいれれば、当たり前ですが勾配は0になるはずですが・・・
|
1 |
glm(Y~-1+X,family=binomial)$coefficients %>% grad_U(log_logistic,.,X,Y) |
実際には数値微分は近似値なので正確には0にはなってくれません。
|
1 |
[1] -0.02424641 -0.01853930 |
数値微分は上でも書いたように、汎用性があってとても便利なのですが、正確性という意味ではちょっと微妙です。もっと正確にする方法もありますが、その分計算時間がかかります。
今回使っている2地点を使った近似の場合、パラメータの数+1回分の対数尤度の計算が必要になります。モデルが複雑になると、この計算量がバカにならなくなり、MCMCで計算時間がどんどん伸びていきます。正確にするために3地点近似をすれば、パラメータ数☓2+1が必要なので、さらに時間は遅くなっていきます。
正確な微分値を求めるためには、もちろん数学的に導関数を導出してやればいいわけですが、Stanのようにオリジナルな確率モデルをユーザーが作る場合には、いちいち数学的に導出するのは困難です。また、パラメータごとに偏導関数が違うため、パラメータの数が増えた場合は結局パラメータ数✕導関数の計算量の時間がかかります。
このような問題を解決するのに自動微分があります。自動微分は、たかだか元の関数の定数倍の計算時間で終わり、かつ、元の関数がなんであっても、正確な微分値を求めることができる方法です。そんな方法があるなんて!
◆自動微分のアルゴリズムいろいろ
自動微分は、対数尤度の関数をそのまま使って、勾配を計算することができる方法です。これを理解するためには、いろいろ説明しないといけないのですが、すみません、僕の理解がまだ中途半端なのと、記事を書く時間が限られてるので他のブログ記事に説明を投げさせてください。
自動微分を行うアルゴリズムには複数あります。
まずは二重数を用いて自動微分をする方法です。
この記事を見てもらえればだいたいわかるかと思うのですが、ポイントは次です。
・二重数という型を定義する(Dual型)
・Dual型での演算を、四則演算や初等関数について新たに定義する
・対数尤度を計算するコードを書いて引数にDual型の変数を入れると、対数尤度と同時にその微分値も得られる
二重数は複素数のように、1つの数値だけど2つの数を含んでいるものです。これを利用すると、元の関数を用意するだけで自動的に微分値も求まるのです。すげぇ。
もう一つは合成関数の微分を利用して、上と同じように演算子を新たに定義することで計算できる方法です。この方法には、ボトムアップの方法と、トップダウンの方法があるようです。次の記事をご覧ください(丸投げ
ボトムアップ型のほうがわかりやすいのでそちらを説明します。トップダウン型はすみません、まだ理解できていません。
まず、合成関数の微分は、次のように関数の導関数と、関数の中の導関数の積で表せます。
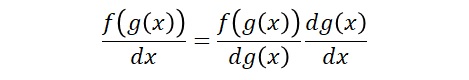
これをふまえ、四則演算と初等関数の微分公式を定義して、それらの組み合わせはすべて合成関数の微分を使って連鎖を考えていけば、自然と微分値の計算ができることになります。
ボトムアップ型はこのように、最初に偏微分したいパラメータを1、それ以外を0と入れた状態であとは基本的な演算と合成関数の連鎖律を利用して微分値を計算する方法です。もとの値からボトムアップ的に計算する、というわけです。
一方トップダウン型はその逆を計算するようなのですが、原理的なところはよくわかってません。
ボトムアップ型の計算量は、各パラメータの数✕元の関数の計算量になるため、実際のところ数値微分とそんなに変わりません(ちょっと少ない)。しかし、正確な微分値を得られる点で自動微分のほうが実用的と言えるでしょう。
トップダウン型は逆に計算する過程の値を全部保存しておかないといけないのでメモリはかなり食うみたいですが、パラメータがどんなに多くても元の関数の計算の定数倍程度の計算量で微分値が求まるようです。つまり、トップダウン型のほうがパラメータが多い場合は高速、ということです。
◆トップダウン型の自動微分を行うパッケージ
Rにもそういうのあるかな、と探してみたらありました。madnessパッケージ。
トップダウン型の自動微分を行えるようです。さっそくやってみましょう。
まずは簡単な数式の微分値を求めてみましょう。
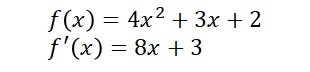
という式を考えます。まずはf(x)とf'(x)をRで書いてみます。
|
1 2 3 4 5 6 7 |
fanc <- function(x){ 4*x^2 + 3*x+2 } d_fanc <- function(x){ 8*x+3 } |
xに5を入れて計算してみると、
|
1 2 3 4 |
> fanc(5) [1] 117 > d_fanc(5) [1] 43 |
このように計算できました。
さて、madnessを使って微分値の計算をしてみましょう。
|
1 2 3 4 |
library(madness) mad_x <- madness(5) fanc(mad_x) |
すると・・・
|
1 2 3 4 5 6 7 8 9 |
> mad_x <- madness(5) > fanc(mad_x) class: madness d (((numeric * (5 ^ numeric)) + (numeric * 5)) + numeric) calc: ----------------------------------------------------------- d 5 val: 117 ... dvdx: 43 ... varx: ... |
valのところにf(x)の値が、そしてdvdxのところにf'(x)、つまり微分値が計算されているのがわかると思います。微分値を取り出したいときは、S4クラスで定義されてるので、
|
1 2 |
temp <- fanc(mad_x) temp@dvdx |
というように、@で取り出します。
パイプ演算子を使えばmadnessを間にいれるだけでコードが書けるので便利です。
|
1 |
5 %>% madness %>% fanc |
madnessでは、madnessクラスのオブジェクトに対して、+とか*などの演算子に適用されるメソッドが区別されていて、いくつかの初等関数と統計関数については導関数が定義されているので、仲の関数が通常のRコードで書かれていれば微分値を自動で返してくれるわけです。
ただ、確率密度関数にいれても、エラーが出ます。
|
1 2 |
> 5 %>% madness %>% dnorm Error in dnorm(.) : 数学関数に非数値引数が渡されました |
よって確率密度関数は自分でRに書き起こさないといけません。先ほどのロジスティック回帰分析の対数尤度関数は自分で書いておいたものなので動くでしょうか。中にはsum()や僕が独自に作ったinv_logit()などの関数も含まれていますが・・・
最尤推定値をRで推定し、その係数ベクトルをmadnessクラスにかえて、対数尤度関数に入れてみましょう。
|
1 2 3 |
glm(Y~-1+X,family=binomial)$coefficients %>% madness %>% log_logistic(X,Y) |
すると
|
1 2 3 4 5 6 7 8 9 |
class: madness d (sum(((numeric * log((numeric / (numeric + exp(-(numeric %*% .)))))) + (numeric * log((numeric - (numeric / (numeric + exp(-(numeric %*% .)))))))), na.rm=FALSE) + numeric) calc: --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- d . val: -135.5688 ... dvdx: -0.0000000000002898792 -0.0000000000008608795 ... varx: ... Warning message: In madness(.) : no dimension given, turning val into a column |
ちゃんと勾配(微分値)が(ほぼ)0になっていますね。正確な微分値が計算できてるとわかります。
ただし、警告が出ています。これはmadnessクラスにかえるときに変数の次元を明示的に書いておけ、という警告です。次のようにベクトルではなく1次元マトリックスとして定義してやればこの警告はでません。
|
1 2 3 4 |
glm(Y~-1+X,family=binomial)$coefficients %>% matrix(nrow=P) %>% madness %>% log_logistic(X,Y) |
◆計算スピードは?
madnessパッケージで自動微分ができることがわかりました。では、数値微分と計算時間を比較してみましょう。
もともとはMCMCのアルゴリズムであるNUTS、あるいはHMCに自動微分をいれたい、というのが目的でした。HMCでは前の記事で紹介したように、Lの回数に比例して勾配を計算しなければなりません。もしL=100にしていたとしたら、1回のMCMCサンプルにかかる時間は100回の微分の計算である程度目安がわかるわけです。
そこでシンプルに100回微分値を求める時間を計算してみました。
まずは数値微分。パラメータは切片と回帰係数の2つです。
|
1 2 3 4 5 |
t<-proc.time() for(i in 1:100){ grad_U(log_logistic,beta,X,Y) } proc.time()-t |
すると
|
1 2 3 |
> proc.time()-t ユーザ システム 経過 0.03 0.00 0.04 |
0.03秒でした。意外にはやいぞ数値微分。
続いて、madnessでの計算。
|
1 2 3 4 5 6 |
mad_beta <- beta %>% matrix(nrow=P) %>% madness t<-proc.time() for(i in 1:100){ log_logistic(mad_beta,X,Y) } proc.time()-t |
ドキドキ。
|
1 2 3 |
> proc.time()-t ユーザ システム 経過 0.26 0.00 0.24 |
0.26秒!おっそ!
というわけで、数値微分のほうが早いという結果に・・・
いや、待て。トップダウン自動微分はパラメータを増やしても高速なんでした。階層モデルではサンプルサイズ分のパラメータを計算しないといけないこともあります。というわけで、ロジスティック回帰の説明変数を99個、つまりパラメータ数を100個にしてみました。
まずはサンプルデータを作ります。
|
1 2 3 4 5 6 7 8 |
##logistic beta <- rnorm(100,0,1) P <- length(beta) N <- 200 X <- MASS::mvrnorm(N,rep(0,P-1),diag(rep(1,P-1))) X <- as.matrix(cbind(rep(1,N),X)) mu <- inv_logit(X%*%beta) Y <- rbinom(N,1,mu) |
数値微分の計算。
|
1 2 3 |
> proc.time()-t ユーザ システム 経過 1.24 0.02 1.27 |
1.24秒。さっきよりパラメータが50倍になってるので、おおよそパラメータ数倍になってるでしょうか。
続いてmadness。
|
1 2 3 |
> proc.time()-t ユーザ システム 経過 0.51 0.01 0.53 |
おお!さっき0.26秒だったのに対して、たったの2倍時間しかかかってない!はやいぞmadness!
◆まとめ
というわけで、madnessパッケージを使えば確率モデルの勾配は(それなりに)早くなることがわかりました。
ただ、ざっと見たところmadnessでは階乗の計算やガンマ関数が実装されてないようで、ポアソン分布とか負の二項分布などは定義できないようです。再帰的な方法とかいろいろ試みましたがうまくいきませんでした。残念。
というわけで、madnessをどんぐりに実装するのはあきらめて、数値微分でやるしかないか・・・と思っているところです。