この記事は、Stan Advent Calendar 2019 10日目の記事です。
今回紹介する話は、僕の研究に関わるところなので、これまでの記事に比べて若干領域限定的な話です。
しかし、結構重要な問題を含んでいるので、「都道府県別のデータで相関みたぜいえーい」っていう感じの人はぜひ見てもらえればと思います。
納豆と牛肉のイケナイ関係
今回はいきなりタイトル回収しました。
実は最近、いろんな関心から都道府県別のデータをながめてたわけです。そういうときに便利なのがこのサイト。学術的にどれくらい正しいか知らないけど、ざっとしたことを知るには便利。
タイトルが若干ゆるいですが、まぁ便利です。
で、いろいろデータを見てたんです。そしたらね、発見しちゃったんです。
納豆と牛肉の消費量にすげぇ相関があることを。
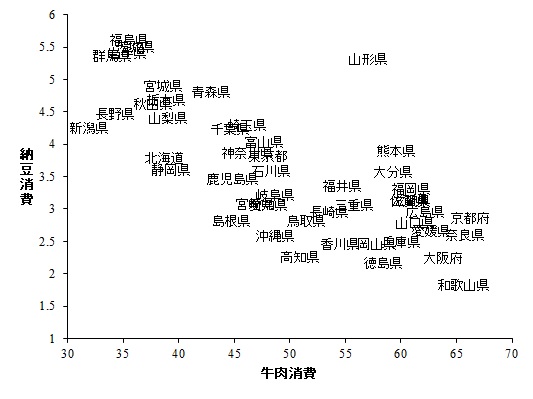
相関係数 r = -.74。見て確信しましたね。「あ、これNatureだわ」って(嘘
これだけ見たら、皆さんどのように解釈しますかね?
「ほら、大豆って畑のお肉っていうし、納豆食べてると牛肉いらないんだよ。タンパク質的に」
とかそういうこと考えちゃいますよね?あれ、そうでもない?
なんとなく見てもらえればわかるんですが、納豆消費は東北地方~関東地方に多く、牛肉消費は近畿~中四国で多いんですね。つまり、東日本では納豆消費が多く、西日本は牛肉消費が多い。面白いのは、山形県は他の東北の県に比べて肉食ってますね。Twitterで「芋煮じゃね?」というご指摘もいただきましたが。
こういうふうに見ると、なるほど食文化が東西で違ってるんだなということが見えてきます。ついでに豚肉は東日本でよく食べられてるので、タンパク質うんぬんは速攻で否定されます(
納豆と牛肉の食文化
食文化は、当然ながら地理的に近いところで近いです。それは、文化は伝搬するからです。ある地域でたまたまある食文化が生まれたとして、それは地理的に近いところに徐々に広がります。
Wikipediaとか適当に調べたところによると、納豆はもともと鎌倉時代のときに東北に戦争に行くときにたまたま茹でたての豆を持っていっちゃって、腐ったからだとか、明治時代に水戸あたりの電車開通のときにお土産戦略として納豆を配ったのだとか、諸説あります。でも、北関東・南東北が納豆文化の出発点であることはいえそうです。
牛肉も適当にWebで調べたところによると、明治に牛肉を食べるのが流行った(西洋文化の輸入?)。加えて、牛を労働力として家畜に使っていたのが関西で、関東や東北は馬を使っていた。牛はよかったが、馬はあまり量が食べられない。代わりに、豚を食べた、とのこと。で、牛を食べる文化は牛がもともと家畜用に生産されていた兵庫を中心に広がったそうな。ほんまかどうかは知りません。
これらの言説が本当かどうかはこの際おいといて、文化は地理的に近いところから広がっていくというのは、文化進化や人類学で明らかにされていることです。
そして問題は、文化は「その文化がそこにあることの機能」とまったく無関係に、文化伝搬を理由に見かけ上の相関が生じうる、ということです。
納豆と牛肉のように。
こういう問題を、Galton問題とよぶようです。Galton問題については、日本語では次の本に解説があります。
Galton問題を簡単に言うと、国別、地域別の文化データ間の相関は、国や地域が歴史を共有している(文化伝搬が起きている)ことによるものなのか、その文化的な機能に関連性があるのかが区別できない、ということです。
すなわち、納豆と牛肉消費に相関があるとして、それは食としての機能に関連があるのか、文化伝搬が生じた結果のものなのか区別ができないのです。
とうわけで、今回は、「都道府県別データで相関見るとき、空間的自己相関をコントロールしないとヤバいかもしれない」という記事です。
あともう一つは推測統計学的な問題もあって、データが相互独立に取得されてない、ということです。地理的に近い場所はデータが似ているので、普通に相関を計算すると標準誤差が過小推定される、というわけです。それも補正する必要があります。
Galton問題をモデリング
あんまり時間がないので(おい、ややこしい話は置いといて、とりあえずGalton問題にどう対処したらいいかを考えます。
まずは普通に回帰分析。比較のため、Stanで書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
data { int N; vector[N] Y; vector[N] X; real beta_scale; real var_scale; real dft; } parameters { real beta; real } model { vector[N] mu = beta*X; target += normal_lpdf(Y | mu, sigma); target += student_t_lpdf(beta | dft, 0, beta_scale); target += student_t_lpdf(sigma | dft, 0, var_scale) - student_t_lccdf(0 | dft, 0, var_scale); } |
一応、あとでモデル比較するためにターゲット記法で書いています。あと、データは標準化していることを前提に書いています。
Rコードは、以下です。データは上のサイトからとってきてください。1行目に納豆、2行目に牛肉のデータ、あとは各都道府県の緯度・経度のデータが入っています。
回帰だけならいらないデータがはいってますが、これらはあとで使うのでここでは無視しておいてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
library(rstan) library(bridgesampling) library(dplyr) library(magrittr) library(geosphere) model.reg <- stan_model("natto_reg.stan") dat_natto <- read.csv("natto.csv") N <- dat_natto %>% nrow Y <- dat_natto[1] %>% scale %>% data.frame X <- dat_natto[2] %>% scale %>% data.frame data.reg <- list( N = N, Y = Y[, 1], X = X[, 1], beta_scale = 1, var_scale = 1, dft = 1 ) fit.reg <- sampling( model.reg, data = data.reg, iter = 12000, warmup = 2000, chains = 4, cores = 4 ) |
推定結果は、次のような感じ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> fit.reg %>% + print(pars=c("beta","sigma")) Inference for Stan model: natto_reg. 4 chains, each with iter=12000; warmup=2000; thin=1; post-warmup draws per chain=10000, total post-warmup draws=40000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta -0.73 0 0.10 -0.93 -0.79 -0.73 -0.66 -0.53 30591 1 sigma 0.69 0 0.07 0.56 0.64 0.68 0.74 0.85 28373 1 Samples were drawn using NUTS(diag_e) at Mon Dec 09 16:41:23 2019. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). |
β=0.73、ととても高い係数が得られました。95%CI見ても、牛肉から納豆消費を強く予測できそうなことがわかります。
続いて、Galton問題のモデリング。
まず文化伝搬は空間的自己相関という形でデータ上に現れるだろう、と仮定します。つまり、地理的に近いところは文化データは「似ている」。
この空間的自己相関は、ガウス過程を使って表現できます。以後、Lee (2017)の論文を参考に、空間的自己相関をコントロールして、牛肉消費から納豆消費を予測できるかを検討してみましょう。
本当は相関を推定できればいいんですが(実際はできるんですが)、ちょっとテクいのと収束が悪かったのでより簡単に説明できる回帰モデルのほうで記事を書きます。
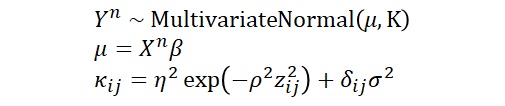
ここで、X,Yはn次元のベクトルでここでは牛肉消費、納豆消費に対応します。βは回帰係数です。κはカーネル関数で、ここではガウスカーネルを想定しています。zは緯度経度から計算された都道府県間の地理的距離です。δ_ijはiとjが等しい場合に1、そうでない場合に0となる関数です。
また、ハイパーパラメータとして、ηとρ、そしてσがあります。η^2はデータYの分散のうち、地理的相関によって説明される分散を意味し、σ^2は残差分散です。ρは自己相関の強さを表すパラメータです。
ここで重要なのは、地理的な距離が遠いほど、データの相関が小さくなる、つまりデータが似ていないということを表現できているということです。
さて、この確率モデルをStanで書くと次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
data { int N; vector[N] Y; vector[N] X; matrix[N,N] dist; real beta_scale; real var_scale; real rho_scale; real dft; } parameters { real beta; real real real } model { vector[N] mu = beta*X; matrix[N,N] Kappa; for(i in 1:N){ for(j in 1:N){ Kappa[i,j] =eta^2*exp(-dist[i,j]*rho^2); if(i==j) Kappa[i,j] += sigma^2; } } target += multi_normal_lpdf(Y | mu, Kappa); target += student_t_lpdf(beta | dft, 0, beta_scale); target += student_t_lpdf(sigma | dft, 0, var_scale) - student_t_lccdf(0 | dft, 0, var_scale); target += student_t_lpdf(eta | dft, 0, var_scale) - student_t_lccdf(0 | dft, 0, var_scale); target += student_t_lpdf(rho | dft, 0, rho_scale) - student_t_lccdf(0 | dft, 0, rho_scale); } |
そして走らせたRコードは以下です。
cdistは都道府県間の距離を格納しています。今回は緯度経度データからgeosphereパッケージのdistm関数を使って計算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
model.GP.reg <- stan_model("natto_GP_reg.stan") cdist <- dat_natto %>% dplyr::select(longitude,latitude) %>% distm(fun=distGeo)/1000000 data.reg <- list( N = N, Y = Y[, 1], X = X[, 1], dist = cdist, beta_scale = 1, var_scale = 1, rho_scale = 2.5, dft = 1 ) fit.GP.reg <- sampling( model.GP.reg, data = data.reg, iter = 12000, warmup = 2000, chains = 4, cores = 4 ) |
分析結果は以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Inference for Stan model: natto_GP_reg. 4 chains, each with iter=12000; warmup=2000; thin=1; post-warmup draws per chain=10000, total post-warmup draws=40000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta -0.12 0.00 0.11 -0.33 -0.19 -0.12 -0.04 0.10 23533 1 sigma 0.14 0.00 0.09 0.01 0.07 0.14 0.21 0.32 18463 1 eta 1.17 0.01 0.68 0.62 0.82 1.00 1.29 2.72 6608 1 rho 1.25 0.00 0.45 0.42 0.93 1.24 1.55 2.16 12130 1 Samples were drawn using NUTS(diag_e) at Mon Dec 09 17:03:38 2019. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). |
ほげぇーβ=-.12。はい、消えたー
というわけで、地理的相関をコントロールすると、牛肉消費が納豆消費を予測する効果が消えました。
ただ、このモデルが「いいかげんなモデル」で、回帰効果が消えたように見えただけかも知れません。そこで、ベイズファクターを使ってモデル比較をしてみます。もちろん、この記事にあるように事前分布に影響を受けるわけですが、今回の例ではそれほど事前分布の影響は大きくないです。
|
1 2 3 4 5 6 7 |
bs.reg <- fit.reg %>% bridge_sampler(method = "warp3") bs.GP <- fit.GP.reg %>% bridge_sampler(method = "warp3") bayes_factor(bs.GP,bs.reg) |
結果は、
|
1 2 |
> bayes_factor(bs.GP,bs.reg) Estimated Bayes factor in favor of x1 over x2: 11742233.09754 |
BF>1億となりました。
つまり、空間的自己相関を統制したガウス過程モデルのほうが非常に強く選択されました。
なお、この結果はハイパーパラメータのρ=2.5の結果ですが、この記事にあるように事前分布に強く影響を受けます。というわけで、1、10、100で試してみましたが、BF>1億5千万、3千7百万、37万という感じでした。結構違いがありますが、ガウス過程モデルのほうがよい、というのは揺るがないようです。
【余談】なお、BFは周辺尤度の比なので、かなり敏感に変動します。よく使われる情報量基準は、周辺尤度を対数とって、符号を反転したものですが、そういう指標だとそれほど変わっていません。上のモデルについては、ρ=2.5のときの37、ρ=100のときは40です。そして、回帰係数の負の対数周辺尤度は53です。このように見ると、BFを計算すると「ぐえー変わりすぎー」と思いますが、まぁそんなもんかな、という感じです。でもBF>3なんていう基準はやっぱ怖いですね。
まとめ
このように、空間的自己相関を考慮せずに文化データの相関を見ると、結構解釈が変わりうるよ、という一例をお見せしました。また、ベイズ統計モデリングでそれをコントロールした分析ができるよ、ということも示しました。
ただし、すべての文化データが空間的自己相関が高いわけではありません。それらは、ちゃんと分析してみないとわからないと思います。
都道府県単位の分析、国単位の分析は、いろいろ罠があるので気をつけようね、というお話でした。