HAD17から、一般化線形混合モデル(GLMM)を用いて分析できるようになりました。
この記事では、GLMMをHADで実行する方法について解説します。
まず、GLMMを実行するためにはソルバーオンバージョンを使う必要があります。ソルバーオフでは実行できないので注意が必要です。
◆HADにおけるGLMM
GLMMは、尤度関数に積分が含まれますが、一般にその積分は解析的には解けません。
そこで、数値的に積分を解くか、何かしらの近似を行う必要があります。数値的に解く方法として、ガウスエルミート求積を使うなどの方法があります。近似する方法は、ラプラス近似を用いる方法が有名です。どちらも多くの場合正確な推定値を与えます。
数値積分を使うときは、計算量が多くなるので回帰係数の変量効果の推定や、複数のクラスターで変量効果を推定するのが難しくなります。一方、ラプラス近似は計算量は少なめなので、統計パッケージでよく使われます。ただ、モデルによっては近似が上手くいかなくなる場合もあります。
HADでは、GLMMをラプラス近似を用いて解いています。ただし、クラスターは1種類しか指定できません。また、推定がものすごい遅いので、データサイズが大きい場合やモデルが複雑な場合は数十分かかることがあります。
◆ポアソン分布の過分散を推定する
久保みどり本で紹介されているような、ポアソン分布を仮定できそうだけど、実際はモデルが想定しているよりもデータの分散が大きい場合のGLMMをやってみます。
例で使うのは、プロ野球選手のHRの本数データです。HRは発生確率がレアで、0以上の離散値をとるデータなので、理屈的にはポアソン分布が当てはまりそうです。しかし、実際にはHRを打てるかどうかは打力の個人差があるので、過分散が生じます。
まずHRのヒストグラム
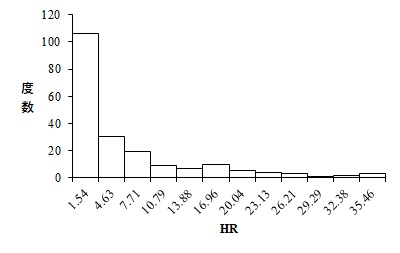
このように、ポアソン分布に比べて分散が大きそうです。
比較対象として、まずポアソン分布を仮定したGLMをHADでやってみます。

上のように、「回帰分析」のなかの「一般化線形モデル」を選び、モデルを「カウント」に設定します。これで分析実行を押すと、
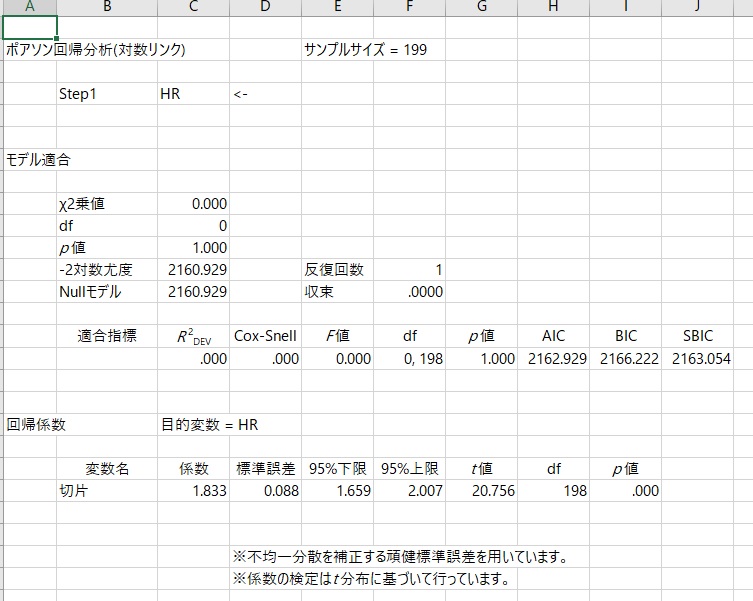
という結果が得られます。AICは2162.929でした。
次に、GLMMを実行してみます。
今度は「一般化線形混合モデル」を選択して、同じく「カウント」を選びます。
説明変数がないのでモデルは空白です。グループというのは変量効果の推定のためのクラスターIDを選択するところです。今回はplayerIDを使うので、B列のID変数と同じなの省略できます。もしID変数以外の変数を指定したい場合は、それを指定します。

このまま「分析実行」を押せば、GLMMが実行できます。
結果は以下のようになります。

AICは1158.904と大幅に小さくなりました。
変量効果の標準偏差は1.201です。HADではlme4パッケージと同様、変量効果の検定結果は出力しません。
また、GLMMではR2乗値なども出力しません。
◆集団と個人の階層性を仮定した分析
いわゆる階層線形モデルを、正規分布以外の分布で実行したい場合です。やり方は全く同じですが、次はPlayer単位ではなく、球団単位で分析してみます。
今度は、ポアソン分布ではなくて二項分布で分析をしてみます。
打数のうちのHITの割合を打率といいます。打率はAVRという変数があるのでそれを直接使ってもいいのですが、せっかくなので二項分布を使ってモデル上で打率を推定してみます。
そして、球団ごとでの打率の違いを考慮に入れながら年齢によって打率が変わるかを見てみましょう。
先ほどと同じように、一般化線形混合モデルを選び、今度は「割合」を選択します。
生起数にHITを、総数に打数であるATbatsを指定します。
モデルには説明変数である年齢(age)を入れます。
さらに、今回は球団単位の効果を見たいので、グループにteamIDを入れました。

これで分析すると、以下のようになります。

年齢の効果はなさそうです。
◆回帰係数の変量効果の推定
次に、回帰係数の変量効果を推定してみます。
ただし、回帰係数の変量効果を推定するのはとても時間がかかるので、注意してください。
ここではHRデータを球団ごとの違いを考慮しつつ、選手の体重でどれほど予測できるかを分析してみます。そのとき、HRを体重が説明できる効果が、球団ごとで異なるというモデルを考えます(意味があるかどうかは知りません)。
このモデルは、以下の図のように、変量効果にweightを指定するだけでOKです。また、回帰係数の変量効果を見たいときは、一般に集団平均で中心化すると推定が安定します。球団による体重の違いがなさそうなら、あまり結果は変わりませんが。

これを実行すると、次のようになりました。

HRに体重が与える効果は、そこそこ球団間差がありあそうです。
推定には25秒程度かかりました。