前回はt検定と一要因計画の方法でしたが、今回はようやく2要因以上の分析の方法です。
HADでは、5要因まで分析できますが、間・内はその範囲であればどのような組み合わせでもOKです。全部参加者間で5要因でも、全部内要因で5要因でも大丈夫。
◆計算時間について
HADは清水のヘタクソなアルゴリズムを使っているせいもあって、計算がSPSSなどに比べると遅いです。計算速度を決めるのは、以下の要因です。
- サンプル数×参加者内要因の全水準数の大きさ
- 全要因の水準数
- 単純主効果の検定方法
- 共変量の有無
まず1と2について。サンプル数と参加者内の水準数の積が、分析で使われるN数になります。これが大きいほど分析に時間がかかります。また、これに全要因の水準数が掛け算的に影響します。例えば、10人のサンプルで、参加者内要因で4水準、参加者間要因で4水準あると、まず10*4=40人相当のサンプル数で、全水準が4*4=16水準、よって、40*16=480ぐらいのデータ規模になることになります。目安として、200人、内要因の水準24、間要因の水準4(つまり200*24*96=460800)の場合、分散分析だけで僕のPCだと1分かかります(僕のPCはCore i7のメモリ8GB)。また、途中で「応答なし」と出ることがありますが、内部ではHADは頑張って計算しているので、慌てず待ってあげてください。
3.は、単純主効果の検定方法を「プールされた誤差項」を選ぶと時間がかかります。水準別のほうが速いです。
4.共変量を入れると、結構遅くなります。使ってるアルゴリズムがかなり違っているためです。
と、話が「やり方」からずれましたが、「続き」では実際に2要因以上の方法を書きます。
基本的なやり方はt検定と同じです。
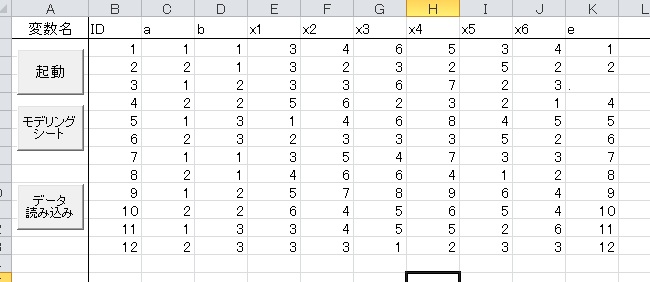
今回は下の図のような12人のデータセットを使います。
◆2要因参加者間要因計画
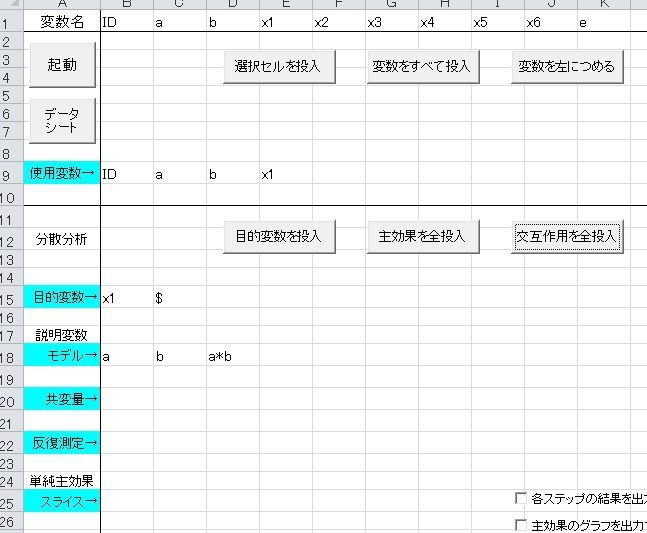
参加者間計画は、使用変数に参加者間要因の水準を識別する変数(上のデータではaとb)を指定し、下の図のようにモデルに投入します。従属変数はx1です。
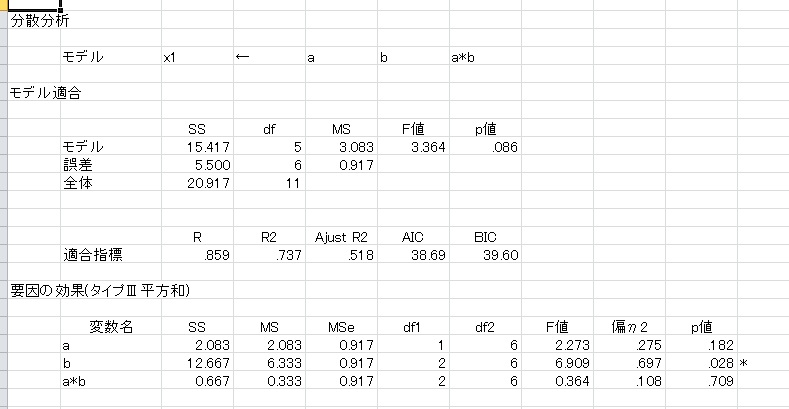
準備はこれだけです。この状態で、「分析実行」をクリックすると、分析結果が出力されます。
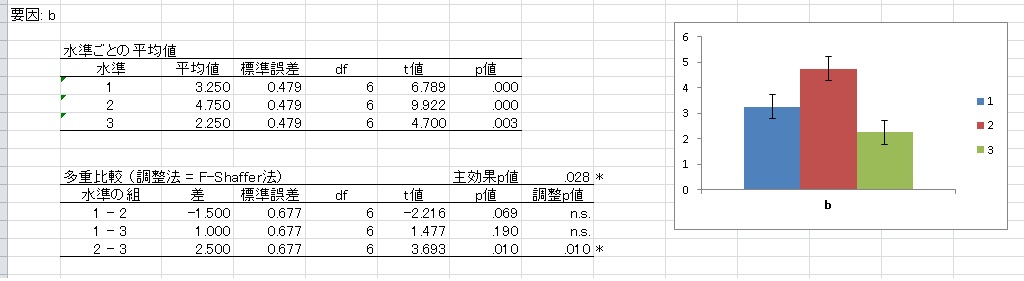
結果を見ると、b要因の主効果が有意だったことがわかります。HADでは、10水準までの主効果について、自動的に多重比較行います。
多重比較の方法は、4種類から選択できます。これらの多重比較についての詳細はANOVA君のページが参考になります。
- Bonferroni法:水準の組の数で有意水準を調整します。3水準の場合、有意水準は0.05÷3=0.0167となります。HADでは、デフォルトでは有意水準ではなく、p値に水準の組数をかけたものを調整p値として出力します。オプションで有意水準を出力するようにすることもできます。また、オプションで指定した多重比較の有意水準よりも高い確率は"n.s."と出力されます。
- Holm法:Bonferroni法はすべての組について、水準の組数で調整しますが、Holm法はt値の絶対値が高い順に調整する値が変わる方法です。たとえば上の図の場合、2-3の組の場合は3で、1-2の組は2で、1-3の組は1で有意水準を割ります。調整する値がt値が小さくなるほど減るので、Bonferroniよりも検出力は高くなります。
なぜこのようなことが可能かというと、もしもっともt値が高い組が有意な場合、上の例では1=3はすでに棄却されてるので、それより小さいt値のペア(1-2など)については組み合わせ数を減らして調整することができる、というわけです。
※HADではHolm法をデフォルトにしています。 - Shaffer法:Shaffer法は、Holm法をさらに改良し、論理的に同時に成り立たないであろう仮説を組み合わせ数から除外して調整する方法です。HADでは、Holland & Copenhaver (1987)に載っている、比較数の上限値早見表にある調整値を利用して、p値を調整しています。
- 修正-Shaffer法:この方法の名前は、正式なものではなく便宜的なものです。修正-Shaffer法は、Shaffer法を改良し、分散分析の主効果が有意だった場合、調整値をさらに小さくできる(p値が大きくならない)というものです。こちらについては入戸野先生の論文を参照してください。Shaffer法の別解として紹介されています。僕もここを参照しました。
さて、次は参加者内要因です。
◆2要因参加者内要因計画
参加者内の場合は、目的変数を複数指定する必要があります。今回の例では、3×2の6水準計画を紹介します。下の図のように、目的変数を6つ指定し、"$"マークのあとに、参加者内要因の要因名を入力します。参加者内要因の要因名は、使用変数にない変数を指定する必要があります。その状態で、「交互作用を全投入」ボタンをクリックすると、自動的に主効果と交互作用が投入されます。
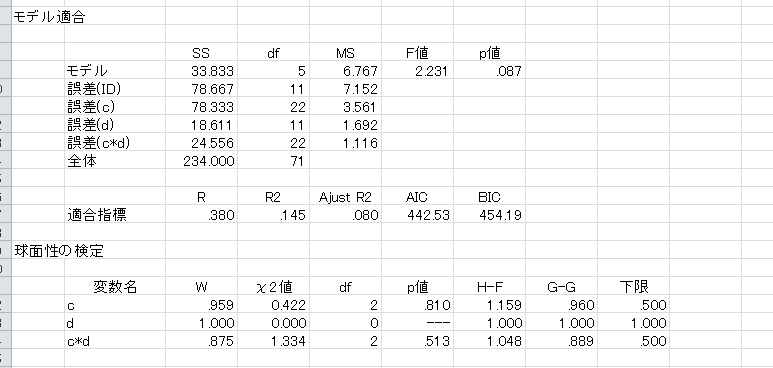
このとき、参加者内要因が2要因以上の場合は「反復測定」と書いてある行に、各水準の水準数を入力する必要があります。下の例の場合、c要因が3水準、d要因が2水準となっています。
なお、c要因とd要因の組み合わせは以下のようになります。
| c要因 | c1 | c1 | c2 | c2 | c3 | c3 |
| d要因 | d1 | d2 | d1 | d2 | d1 | d2 |
| 目的変数 | x1 | x2 | x3 | x4 | x5 | x6 |
つまり最初に指定した要因から順番に、入れ子の構造になるというわけです。この状態で「分析実行」を押すと、分析が開始されます。
参加者内要因では、要因ごとで誤差項が異なるのでそれぞれ表示されます。
また、3水準以上の要因についてはMauchlyの「球面性の検定」が行われます。球面性とは、「参加者内要因の各水準間の"差"の分散がすべて等しい」という状態で、分散分析が正しく計算されるための条件の一つです。Wは、球面性からの逸脱度を表し、0~1の間の値を取ります。1に近いほど球面性仮定が満たされていることを、0に近づくほど球面性から逸脱していることを意味します。
また、球面性から逸脱した場合は自由度の補正を行う必要があります。HADでは以下の補正方法をオプションで選択できます。
- 下限:自由度を理論的に最も小さくなるように設定します。ただ、この方法はやや保守過ぎる方法です。
- G-G:Greenhouse-Geisserのイプシロンに基づいて補正します。上の図のG-Gの値を自由度に乗じて補正します。G-Gは下限値から1までの値を取ります。
- H-F:Huynh-Feldtのイプシロンに基づいて補正します。H-FはG-Gをサンプル数に応じて補正したもので、サンプル数が小さい場合にG-Gが小さすぎる値を出してしまう点を修正します。サンプル数が大きければH-FとG-Gはほとんど違いはありません。また、H-Fは1を超える場合がありますが、その場合は1を乗じる(つまり補正なし)ことになります。
◆2要因混合計画
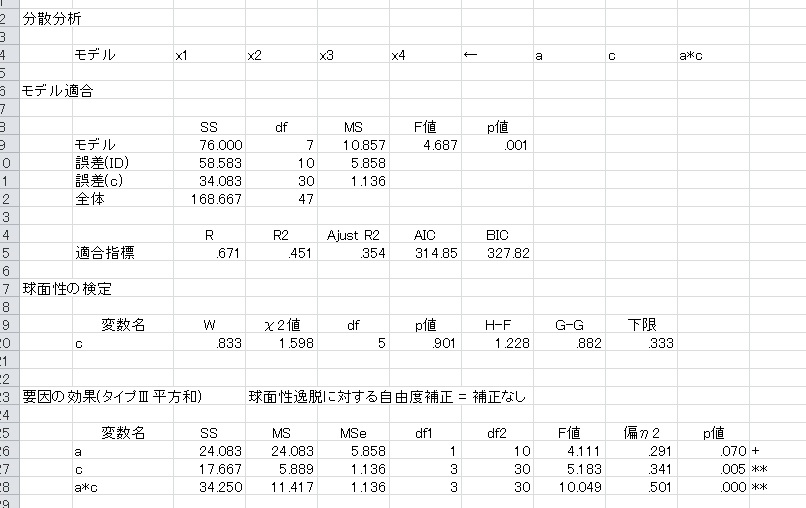
混合計画の場合は、上の二つの方法を組み合わせればできます。例えば、参加者間要因としてaを、参加者内要因としてx1-x4をまとめてcとした場合、下のようになります。
参加者内要因が1要因の場合は、「反復測定」のところには水準数を入力する必要はありません。この状態で「分析実行」をクリックすると、以下のような結果が出ます。
間要因のa要因は、誤差(ID)が誤差項になり、内要因のc要因とa×c交互作用は誤差(c)が誤差項になります。