最近因子分析についてあれこれ勉強していたら、非反復推定による因子分析法というのがあるのを知りました。
Ihara & Kano (1986) A new estimator of the uniqueness in factor analysis. Psychometrika, 51, 563-566.
上記の論文に掲載されている、反復推定を行わない因子分析の方法です。
一般的に因子分析で使われる推定(最尤法や最小二乗法)は、目的関数を最適化するために反復推定を行います。何度も計算して、徐々に最適な値になるように近づけていくわけです。
しかし、この非反復推定法は反復計算をせず、行列演算で解を求めるようです(詳しいことはわかりません)。
とはいえ、この方法の特徴は計算方法が違う、というだけではありません。なんと不適解がほとんど出ないのです。
最尤法で因子分析をすると、共通性が1を超える(つまり、独自性の分散が負になる)ことがままあります。これを不適解と呼びます。分散は定義上負の値になることがないからです。最尤法はとても優れた推定法ですが、この不適解が非常に多く出るので、たまに困ったことになるわけです。
もちろん、不適解は推定法の問題というよりはモデルが不適であることも原因の一つなので、
一概に悪いというわけではありません。モデルが不適切であることを教えてくれるわけなので。
しかし、サンプルサイズが小さいといった理由で不適解になってしまうと、データを取り直さないといけないので大変です。
なので因子分析の推定法は、不適解が出にくいに越したことはないです。
そこで、この非反復推定法の登場、というわけです。実際よく似た方法はいくつかあるようなのですが、今回は狩野先生の方法を紹介します。
詳しくは続きで。
非反復推定法の特徴
まず、推定量の性質について。
非反復推定法は、一致性と漸近正規性という性質を持っています。一致性とは、サンプルサイズを大きくしていくと母集団の真の値に近づいていく、という性質です。推定量にとっては基本的な性質なので、まぁないと困る、というものではあります。次に漸近正規性は、サンプルサイズを大きくしていくと推定量が正規分布に近づいていく、というものです。推定値の検定などを行う時に重要な性質です。
では最尤法と何が違うかといえば、最尤法はそれに加えて漸近有効性という性質を持っています。これは、サンプルサイズが大きくなれば、最尤法が最も標準誤差が小さな推定量であることを意味しています。しかし、非反復推定法は小~中程度のサンプルサイズの場合、最尤法と同じかよい推定をするようです。
実際に僕もシミュレーションをしてみましたが、サンプルが小さいと最尤法よりも真値に近い推定をすることがあります。また、非反復推定法は因子数を過大に見積もって推定しても、一致性を保つことがわかっています。
最尤法は因子数を過大に見積もると不適解が出たり、共通性を過大に推定したりすることがあるようです(詳しいことはわかりません)。それに対して非反復推定法は因子数の過大推定に対して頑健であるといえそうです。
ただし、逆に因子数を真の因子数よりも小さめに推定すると、共通性はかなり小さく推定されるような気がします。実際に最尤法と比べると真の因子数よりも小さい場合、共通性の合計は小さいです。
上記の特徴から、共通性は最尤法に比べると、全体的に小さめに推定されます。不適解がでないことと関係しているのかもしれません。特に因子数が多くなっても共通性があまり変わらないのは、不適解が出ないことの根拠になっているようです。このことから、因子負荷量やω係数なども全体的に小さめになります。
次に、非反復推定法は尺度不変の因子負荷量を推定します。
尺度不変とは、相関行列を分析しても、共分散行列を分析しても同じ結果を与える性質のことです。分散が大きく異なる変数が含まれている場合、最小二乗法や反復主因子法は尺度構成においてあまりいい結果を出しません。最尤法や一般化最小二乗法、そしてこの非反復推定法は尺度不変なので、その心配はないです。
あと、計算が速いです。最大法と平均法があるのですが、最大法はとても速いです。逆に平均法は結構遅いです。
HADではデフォルトは最大法を使ってます。ただ推定量としては平均法のほうがよいようです。
また、最大法は稀に不適解が出るようです。しかし平均法はほとんど出ないようです。僕はいろんなデータを分析してみましたが、平均法で不適解を見たことが一度もないです。最大法は一度だけありました。
まとめると、
- 不適解がほとんど出ない
- 尺度不変
- 小さめのサンプルサイズのときに効力を発揮
- 因子数が多めでも安定して共通性を推定する
- 推定値は最尤法より全体的に小さめになる
- 最大法は計算が速い
こんな感じです。
非反復推定法に対応しているソフトウェア
あまり知られてない方法なので、対応しているソフトはほとんどありませんが、CEFAというフリーの因子分析用ソフトが対応しています(PACEという方法を選ぶ)。この方法はIhara & Kano(1986)そのものではないようですが、最大法とほぼ一致するとのことです。
あとはHAD9.2に搭載予定です。狩野先生からVBプログラムの移植許可をもらいました。
今のところ正常に動いています。むしろ計算が速くて驚いています。
新しい因子数決定の基準を思いついた
以下はおまけです。
先ほど述べたように、非反復推定法は共通性の推定において、因子数を過大に推定した場合は頑健ですが、過少の場合は小さめに推定するようです。しかし、この特徴を使って因子数を決定する新しい基準を考えてみました。
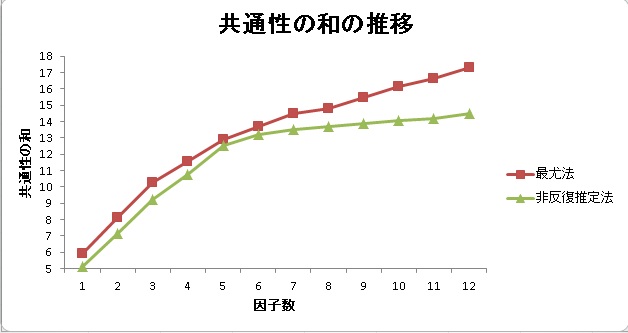
真の因子数が5因子である25個の変数を正規乱数で作成しました。そのデータを最尤法と非反復推定法で因子分析し、共通性の和をプロットしてみたのが下の図です。
真の因子数である5因子のときに最尤法と非反復推定法はほぼ一致しているのがわかると思います。そして、5より小さい場合と5より大きい場合、最尤法のほうが共通性の推定は大きいです。つまり、最尤法は因子数が少なくてもそれなりに共通性を推定し、過大の場合はどんどん大きくなっていきます。それに対して非反復推定法は真の因子数以上では共通性は安定した推定を行い、それより小さい場合はどんどん小さくなっていきます。
これを利用して考えると、最尤法と非反復推定法の共通性の和が最も近いポイントが真の因子数になる、というわけです。ただ、それだと計算量がハンパない上に、最尤法は不適解が出る場合が多いため、次のような方法を考えてみました。
非反復推定法だけのプロットを見てみると、
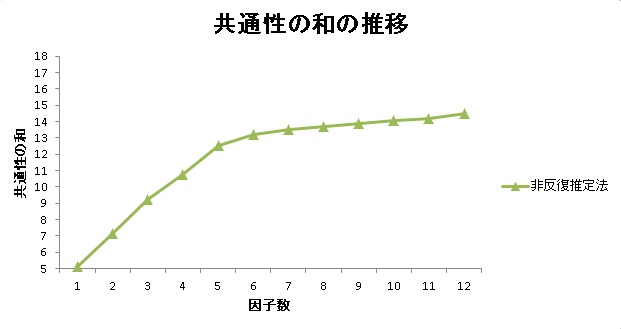
上の図のように、真の因子数でカクンと折れ曲がっています。それは、過剰推定に対して頑健だからだと思われます。つまり、共通性の和のプロットの折れ曲がった点が真の因子数の推定値として使えそうです。
HAD9.2(近日アップ予定)では、これを利用した因子数の提案法を搭載してみました。
アルゴリズムは、回帰分析を繰り返して変曲点を求め、変曲点に最も近い因子数を提案する、というものです。
いろんなデータを分析してみたところの感じとしては、
- MAPに近いが、因子間相関が高い(.50以上)場合は、MAPは少なく提案するが、この方法は正しい因子数を提案する。
- 一つの因子に3項目以上負荷していないと、一つの因子として提案しない。つまりマイナー因子はあまり検出しない。
- サンプルサイズが多い方がクリアに変曲点がわかるが、サンプルサイズによって提案数は変わらない。
- 平行分析よりは良い推定をする。2.と関連して、対角SMCは拾うがこの方法では検出できない因子がたまにある。
- MAPより多く、対角SMCよりは少ない因子数を提案することが多いため、この二つの提案が割れた場合に使えそう。
こんな感じです。とはいえ、ちゃんとシミュレーションとかしてないので、あんまり信じないでください。
特筆すべき点は1と3で、因子間相関やサンプルサイズにあまり影響を受けないところはおもしろいです。
この提案方法のいい点は、すべての因子数ごとにちゃんと因子分析をしている、という点です。
スクリープロットは共通性の推定をしていません。MAPも因子ではなく主成分を使っています。
因子数を推定する、という目的においてちゃんとそれぞれの因子数に対応する共通性を推定して、そこから提案するところが従来法と違うところです。
欠点ももちろんあって、ゴミが多いデータ(誤差相関があったり、マイナー因子があるなど)の場合は上手くいかないこともあります。具体的には、プロットがほぼまっすぐになってしまって、変曲点が見つからないことがあります。変曲点がうまく見つからない場合は変なところを提案します。その場合は、自分でプロットを確認してみるのも必要です。あるいは最尤法と比較するのもいいと思います。逆に言えば、変曲点がはっきりしているときは使える方法だといえると思います。
また、HADではデフォルトは最大法で計算してますが、平均法を使っても可能です。最大法では変曲点がうまく見つからないときも、平均法だときれいに見つかることもたまにあります。ただ、平均法はかなり時間を必要とするので、基本は最大法でいいと思います。
実際のデータで試してみる
では試しに、実際に調査で得たデータを分析した例を示してみます。
分析したのはKiSS18という社会的スキルの尺度で、1400人のデータです。これまでの研究ではいろんな因子数が報告されていて、2因子~6因子ぐらいに分かれるといわれています。
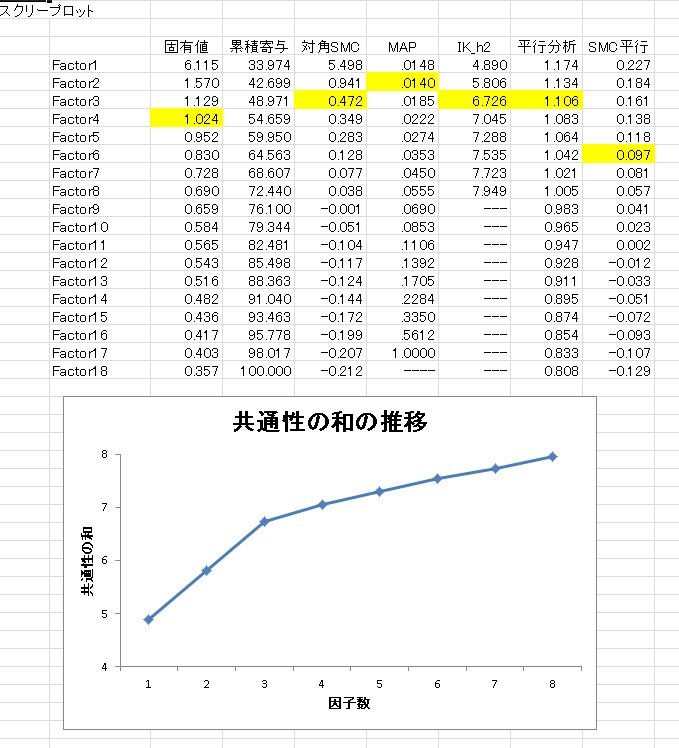
このデータのスクリープロットと、因子数決定の基準としてMAP、平行分析、対角SMC平行分析、そして新しい基準(IK_h2がそれです)の提案を示しています。各基準の提案数は黄色になっているところです。
上の図からわかるように、MAPは2因子を、対角SMC平行分析は6因子を提案していて、先行研究が示してきたような範囲で因子数が提案されています。それに対して新しい基準は3因子を提案しています。プロットを見ると、3因子のところでカクッと曲がっているのがわかります。
このことから、真の因子数は3である可能性が高そうです。
実際に最尤法プロマックス回転で3因子解を計算すると、解釈可能な因子構造でした。
また因子間相関が高く、.45~.65程度です。そのためMAPが少なめに提案している可能性があります。ただ、2因子解でも、同様に解釈は可能だったので、どちらがいいのかは決めかねるところではあります。
真の因子数は誰にもわからないので何因子が妥当なのかは、実際とのところ理論的な仮定や解釈可能性などによって決定すべきだと思います。機械的な提案方法はあくまでその補助程度にとどめておくべきでしょう。