Stanの記事ばっかりですみません。Stan好きなんです。
さて、最近研究で項目反応理論を使っているので、そのあたりのモデルばっかりやってるんですが、今回はあまり知られていない展開型項目反応理論について紹介します。
累積型と展開型
項目反応理論はこちらの記事で少し触れているので、そっちを見てもらえればいいのですが、学力を推定するための統計モデルです。テストにおける正解・不正解という2値の反応に対して、潜在的な変数である学力が影響すると考えます。例えば下の図のように、学力が高くなると正答率が高くなる、という関係をロジスティックカーブで表現したりします。
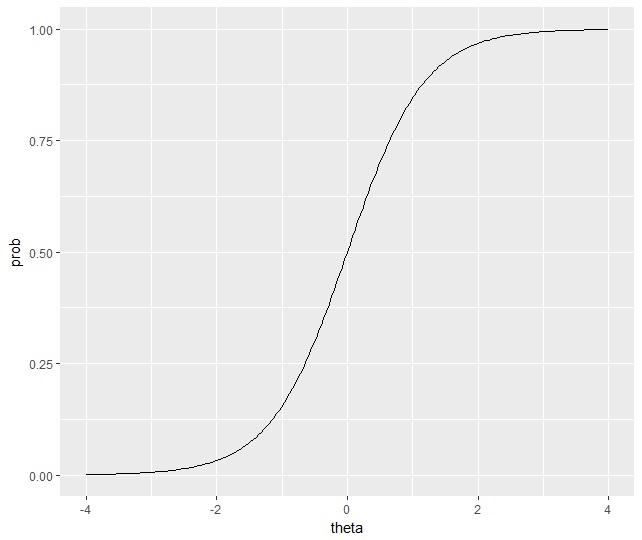
項目反応理論では一般に、潜在変数である学力が高くなるほど、問題への正答率が高くなると考えます。つまり、項目反応関数は単調増加であると仮定するわけです。
学力と正答率の関係に単調増加を仮定するのは自然だと思うのですが、好き―嫌いのような評価だったらどうでしょうか。たとえば潜在変数が甘いものが好きな程度で、反応があるお菓子に対する好き・嫌いを評定するものだとします。すると、自分の好みより甘すぎる対象に対しても、甘さが足りないものに対しても「好き」と答える確率は低くなり、自分の好みにぴったりのものに対して「好き」と答える確率が高くなるはずです。
そのような場合、項目反応関数は次のように山型になることが想定できます。
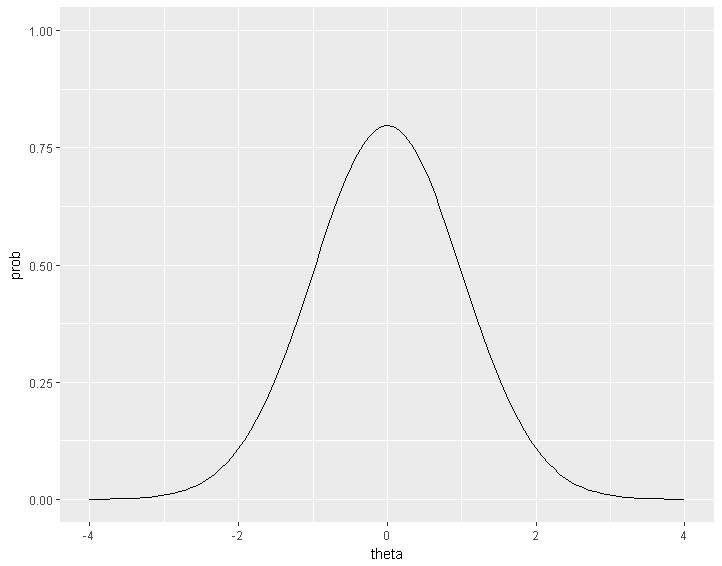
このように、項目反応関数には二つのタイプがあることがわかります。単調増加になるタイプのものを「累積型」、ピークをもつものを「展開型(Unfolding)」と呼びます。政治的態度や官能評価など、回答者の好みの位置と対象の位置の距離に比例して反応しやすくなるようなタイプ(心理学でいうところの態度測定)は、展開型の項目反応関数が合っているといえます。
段階展開型モデル
さて、項目反応理論は2値だけでなく、多値の順序尺度に対して適用できるモデルが複数提案されています。それはSamejimaの段階反応モデル(Graded Response Model:GRM)とMurakiの一般化部分採点モデル(Generalized Partial Credit Model:GPCM)です。どちらも累積型に該当する項目反応理論になります。
GRMやGPCMの「累積型」は項目反応関数は以下のようになります。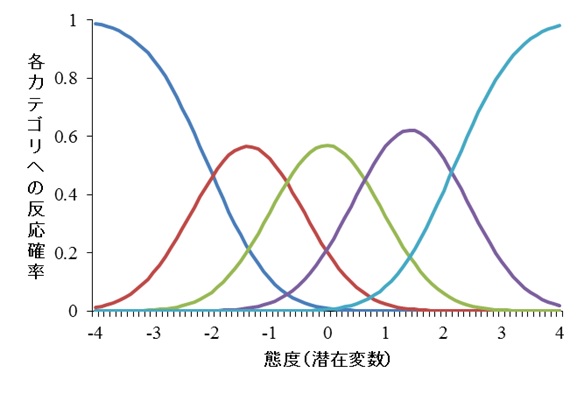
左のカーブが最も反応段階が低いカテゴリへの反応確率で、そこから右に行くにつれて高い反応段階になっていきます。上は5件法の場合の項目反応関数です。
それに対して展開型にも多値の順序尺度に適用できるモデルが提案されています。それはRoberts, Donoghue, & Laughlin(1998)の一般化段階展開型モデル(Generalized Graded Unfolding Model:GGUM)です。
GGUM、つまり「展開型」の多値バージョン項目反応関数は下のようになります。
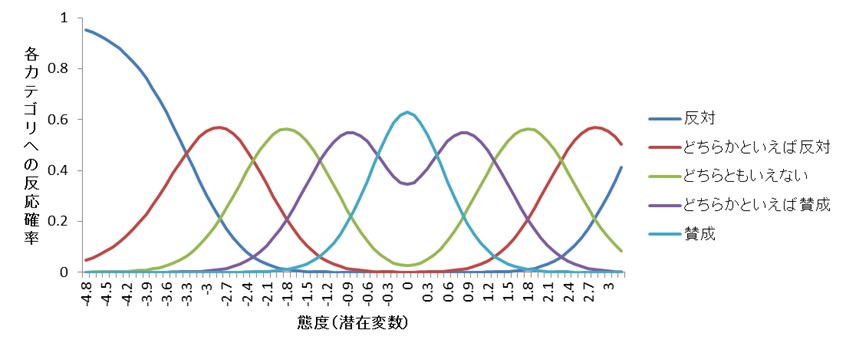
最適な点で「賛成」というカテゴリへの反応確率が最も高くなり、そこから離れるにつれて「賛成」への反応確率が下がっていきます。そして、「どちらかといえば賛成」に対する反応確率が増えていきます。対象との距離が遠い(正・負ともに)場合に、「反対」というカテゴリへの反応確率が高くなっているのがわかります。
対象への好みや、社会的態度など、対象と自分の立ち位置の距離をリッカート尺度で測定したい場合、GGUMの項目反応関数のほうが適切に潜在変数(好みや態度)を推定できるかもしれません。
今回は、このGGUMをStanで推定する方法を紹介します。
GGUMの確率モデル
GGUMは多値バージョンの項目反応理論なので、データがカテゴリカル分布に従うと考える点はGRMやGPCMと同じです。つまり、
![]()
そして、反応確率Pijは次の確率モデルで表現します。かなり複雑なのでぱっとみで理解するのは大変です。
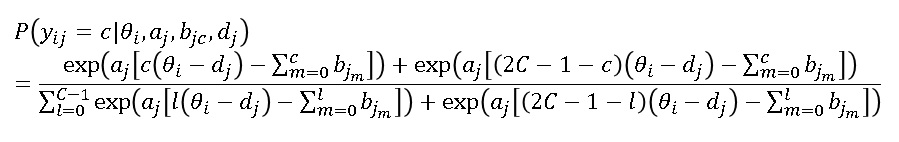
まずθは潜在変数、aは識別力パラメータ、bは閾値パラメータ、dは位置パラメータです。識別力は大まかにはGRMやGPCMと同じ意味で解釈できます。閾値bはθ―dを中心とした場合の各カテゴリの反応確率が逆転する位置を意味しています。dは対象(項目)の潜在空間上の位置を意味しています。また小文字のcは各反応カテゴリで、大文字のCは全体の反応段階数です。
GGUMはGPCMを発展させたものなので、詳細を理解したい場合はGPCMから調べてみてください。豊田先生の項目反応理論中級編などに書いています。
最後に、θについては事前分布を仮定しないとうまく収束しません。ここは項目反応理論で一般に用いられている標準正規分布を仮定します。
![]()
Stanコード
上の確率モデルをStanで表現します。まずはモデル通りに書いたバージョンです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
data { int int int int y[N,P]; // observations } transformed data{ vector[S] c = cumulative_sum(rep_vector(1,S))-1; } parameters { real theta[N]; real vector[S-1] b[P]; real d[P]; } model { vector[S] thr[P]; //prior theta ~ normal(0,1); a ~ student_t(4,0,5); for(p in 1:P) b[p] ~ normal(0,10); d ~ normal(0,10); //model for(p in 1:P){ thr[p] = cumulative_sum(append_row(0,b[p])); } for (n in 1:N){ for(p in 1:P){ vector[S] prob; vector[S] temp1 = a[p]*(c*(theta[n]-d[p])-thr[p]); vector[S] temp2 = a[p]*((2*S-1-c)*(theta[n]-d[p])-thr[p]); for(s in 1:S){ prob[s] = log_sum_exp(temp1[s],temp2[s]); } y[n,p] ~ categorical_logit(prob); } } } |
Nはサンプルサイズ、Pは項目数、Sは反応段階数です。つまり、上のコードでは、モデル式でいうところの大文字のCをSで書いてます。あとはモデルのままです。
最後に使っているcategorical_logitは、内部にソフトマックス関数を含んでいるcategorical分布です。分子の部分の対数をこの関数に入れてやればそのまま推定できます。
パラメータリカバリ
このモデルに従って乱数データを生成したい場合は、次のStanコードを使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
data{ int N; int P; int S; real a[P]; vector[S-1] b[P]; real d[P]; } parameters{ real theta; } model{ theta ~ normal(0,1); } generated quantities{ int y[P]; vector[S] temp1; vector[S] temp2; vector[S] thr; vector[S] c = cumulative_sum(rep_vector(1,S))-1; for(p in 1:P){ vector[S] prob; thr = cumulative_sum(append_row(0,b[p])); temp1 = a[p]*(c*(theta-d[p])-thr); temp2 = a[p]*((2*S-1-c)*(theta-d[p])-thr); for(s in 1:S){ prob[s] = log_sum_exp(temp1[s],temp2[s]); } prob = softmax(prob); y[p] = categorical_rng(prob); } } |
Rコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#stan model model.random <- stan_model("GGUM_rando.stan") #setting P <- 25 #項目数 S <- 5 #尺度の段階数 disc <- 1.7 #識別力初期値 diff <- seq(3,-3,length.out = P) #位置初期値 thr <- c(-3.3,-2.3,-1.3,-0.3) #閾値初期値 a_true <- rep(disc,P) b_true <- matrix(nrow=P,ncol=S-1) for(i in 1:P) b_true[i,] <- thr d_true <- diff #data generation N <- 1500 #サンプルサイズ data.random=list(N=N,P=P,S=S,a=a_true,b=b_true,d=d_true) rdata <- sampling(model.random,data=data.random,iter=N,warmup=0,chains=1) dat2 <- as.data.frame((rstan::extract(rdata)$y)) theta_true <- as.data.frame((rstan::extract(rdata)$theta)) |
dat2に乱数データが格納されます。
これを上のStanコードで推定できるか確認しましょう。
Rコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 |
#Stan用データリスト S <- 5 #尺度の反応段階 N <- nrow(dat2) P <- ncol(dat2) datastan <- list(K=K,N=N,P=P,S=S,y=as.matrix(dat2)) #stan model model_GGUM <- stan_model("IRT_GGUM1.stan") #vb vb.GGUM <- vb(model_GGUM,data=datastan,iter=5000,tol_rel_obj=0.0005) |
上では変分ベイズを使っていますが、もちろんMCMCでも推定可能です。ただ、MCMCの場合は位置パラメータdの符号が逆転する不定性が残ってしまうため、Chainによって結果が違ってしまう可能性があります。それを避けるためには、まず変分ベイズで推定したすべてのパラメータを初期値に入れて、MCMCで推定するといいです。モデルが適合していないなどの問題がない限り、すべてのChainで符号は一致した結果が得られると思います。
1500人25項目で、僕のラップトップで1000回の計算が120秒程度でした。結構時間かかります。MCMCだと数時間はかかると思います。
推定された位置パラメータ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
mean sd 2.5% 25% 50% 75% 97.5% d[1] 3.50 0.03 3.45 3.48 3.50 3.52 3.56 d[2] 3.16 0.02 3.12 3.14 3.16 3.18 3.21 d[3] 2.69 0.03 2.63 2.67 2.69 2.71 2.75 d[4] 2.46 0.02 2.42 2.45 2.46 2.48 2.50 d[5] 2.18 0.03 2.13 2.16 2.18 2.19 2.23 d[6] 2.04 0.02 1.99 2.02 2.04 2.05 2.08 d[7] 1.79 0.03 1.73 1.77 1.79 1.81 1.85 d[8] 1.37 0.02 1.33 1.36 1.37 1.39 1.42 d[9] 1.21 0.02 1.16 1.19 1.21 1.23 1.26 d[10] 0.91 0.03 0.86 0.89 0.91 0.93 0.97 d[11] 0.69 0.02 0.64 0.67 0.69 0.70 0.74 d[12] 0.34 0.03 0.29 0.32 0.34 0.35 0.39 d[13] 0.04 0.02 -0.01 0.02 0.04 0.06 0.09 d[14] -0.18 0.03 -0.24 -0.20 -0.18 -0.16 -0.12 d[15] -0.46 0.03 -0.52 -0.48 -0.47 -0.45 -0.41 d[16] -0.75 0.03 -0.81 -0.77 -0.75 -0.73 -0.70 d[17] -1.03 0.03 -1.08 -1.05 -1.03 -1.01 -0.98 d[18] -1.26 0.02 -1.31 -1.28 -1.26 -1.25 -1.21 d[19] -1.55 0.03 -1.60 -1.57 -1.55 -1.54 -1.50 d[20] -1.85 0.02 -1.89 -1.86 -1.85 -1.84 -1.81 d[21] -2.14 0.03 -2.20 -2.16 -2.14 -2.12 -2.09 d[22] -2.54 0.03 -2.59 -2.56 -2.54 -2.52 -2.49 d[23] -2.78 0.02 -2.82 -2.79 -2.78 -2.76 -2.73 d[24] -3.28 0.03 -3.33 -3.30 -3.28 -3.26 -3.23 d[25] -3.19 0.03 -3.25 -3.21 -3.19 -3.17 -3.14 |
だいたいはうまく推定できてると思います。MCMCだともっと精度よく推定できるはずです。
周辺化による高速バージョン
上のバージョンは比較的元のモデルに忠実にコードを書いたものでしたが、これだとサンプルサイズが大きい場合にかなり時間がかかります。そこで、thetaを周辺化して項目パラメータのみを推定してみます。そのあとで、生成量として潜在変数を計算する方法をやってみます。
ポイントは潜在変数が平均0標準偏差1の標準得点になると仮定しているので、-4から4ぐらいの範囲で十分大きな数(といっても20ぐらいでいい)で区切り、区間求積で周辺化している点です。各区間ごとに必要な対数確率の計算を事前に行っておけば、あとは回答者の反応に合わせた対数確率を放り込むだけでいいので、計算がスピードアップできます。この方法はサンプルサイズが大きくなるにつれて速くなります。あと、推定するパラメータも減るので推定が安定する(収束も早い)点も利点です。
Stanコードは以下です。こちらの方法だと、VB1000回の計算時間は30秒程度になります。4倍ぐらい速いです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
data { int int int int int y[N,P]; // observations } transformed data{ real h; vector[K] theta; vector[K] log_pi; vector[S] c = cumulative_sum(rep_vector(1,S))-1; h = 8/(K-1.0); for(k in 1:K){ theta[k] = -4+h*(k-1); log_pi[k] = normal_lpdf(theta[k]|0,1)+log(h); } } parameters { real vector[S-1] b[P]; real d[P]; } transformed parameters{ vector[N] log_lik; vector[N] score; { vector[S] thr[P]; vector[S] log_prob[P,K]; #log probability for(p in 1:P){ thr[p] = cumulative_sum(append_row(0,b[p])); } for (k in 1:K) { for(p in 1:P){ vector[S] temp1 = a[p]*(c*(theta[k]-d[p])-thr[p]); vector[S] temp2 = a[p]*((2*S-1-c)*(theta[k]-d[p])-thr[p]); for(s in 1:S){ log_prob[p,k][s] = log_sum_exp(temp1[s],temp2[s]); } log_prob[p,k] = log_softmax(log_prob[p,k]); } } #likelihood { vector[K] theta_ind[N]; for (n in 1:N){ vector[K] ps = log_pi; for (k in 1:K){ for(p in 1:P){ ps[k] = ps[k] + log_prob[p,k,y[n,p]]; } } log_lik[n] = log_sum_exp(ps); theta_ind[n] = softmax(ps); score[n] = theta_ind[n]'*theta; } } } } model { #prior a ~ student_t(4,0,5); for(p in 1:P) b[p] ~ normal(0,10); d ~ normal(0,10); #model target += sum(log_lik); } |
Kには区切る数を入れます。今回は17個にしてます。
推定結果はだいたい同じです。ちょっとだけ違いますね。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
mean sd 2.5% 25% 50% 75% 97.5% d[1] 3.31 0.02 3.26 3.29 3.31 3.32 3.35 d[2] 3.05 0.03 3.00 3.03 3.05 3.07 3.10 d[3] 2.63 0.03 2.58 2.61 2.63 2.64 2.68 d[4] 2.41 0.03 2.35 2.39 2.41 2.43 2.45 d[5] 2.06 0.03 2.01 2.05 2.06 2.08 2.12 d[6] 1.97 0.03 1.92 1.95 1.97 1.99 2.02 d[7] 1.75 0.02 1.70 1.73 1.75 1.76 1.79 d[8] 1.37 0.02 1.32 1.35 1.36 1.38 1.41 d[9] 1.15 0.03 1.10 1.13 1.15 1.16 1.20 d[10] 0.93 0.02 0.89 0.92 0.93 0.95 0.97 d[11] 0.65 0.03 0.60 0.64 0.65 0.67 0.70 d[12] 0.32 0.02 0.27 0.30 0.32 0.34 0.37 d[13] 0.08 0.02 0.04 0.06 0.08 0.09 0.12 d[14] -0.18 0.03 -0.23 -0.19 -0.18 -0.16 -0.13 d[15] -0.37 0.02 -0.42 -0.39 -0.37 -0.35 -0.32 d[16] -0.70 0.03 -0.75 -0.72 -0.70 -0.69 -0.65 d[17] -0.93 0.03 -0.98 -0.95 -0.93 -0.92 -0.88 d[18] -1.18 0.02 -1.22 -1.20 -1.18 -1.17 -1.14 d[19] -1.44 0.03 -1.49 -1.46 -1.44 -1.42 -1.39 d[20] -1.65 0.03 -1.70 -1.67 -1.65 -1.63 -1.59 d[21] -1.92 0.02 -1.97 -1.94 -1.92 -1.91 -1.88 d[22] -2.34 0.02 -2.39 -2.36 -2.34 -2.33 -2.30 d[23] -2.60 0.02 -2.64 -2.62 -2.60 -2.59 -2.57 d[24] -3.22 0.03 -3.28 -3.24 -3.22 -3.21 -3.18 d[25] -3.07 0.03 -3.13 -3.09 -3.07 -3.04 -3.01 |
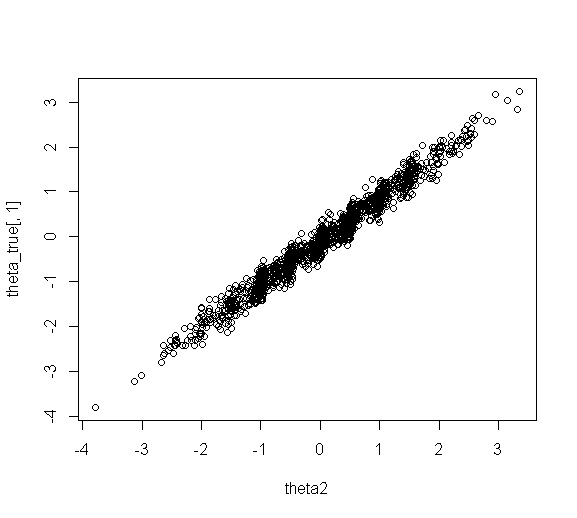
なお、両方コードで推定されたthetaは、真値との相関が0.985程度でした。十分復元できてるかなと思います。