この記事は、Stan advent calendar 2018の7日目の記事です。
Stan、すばらしいソフトですね。今日はStanがいかに素晴らしいかを語る記事です。StanにはNUTSというアルゴリズムが搭載されいているのはご存知だと思いますが、今回の記事は、
Stanを使ってRにNUTSを実装する
という話です。「ちょっと何言ってるかわかんない」、とか言わない。
さて、NUTSはマルコフ連鎖モンテカルロ法(MCMC)の手法の一つ、ハミルトニアンモンテカルロ法(HMC)を発展させたものだ、というのは聞いた人も多いと思います。そこで、MCMCやHMCについて簡単に説明したあと、Stanが搭載しているアルゴリズムについて解説していきます。
なお、数式とかは使わず、全部日本語で説明していきます。数式で詳しいものはいくらでもあるので、そちらをご参考ください。たとえばこちら。
◆マルコフ連鎖モンテカルロ法
ベイズ統計では推定するのはパラメータの事後分布です。それを解析的に求めるのは困難なので、事後分布からの乱数を生成することで近似的に推定する方法がよく使われます。それをマルコフ連鎖モンテカルロ法(MCMC)といいます。
MCMCはマルコフ連鎖を使って事後分布からの乱数を生成するアルゴリズムです。簡単に言えば、パラメータの初期値を決めて、その値から推移確率(ある値から別の値に推移する確率)に従って次のパラメータを乱数によって生成し、それを繰り返していきます。すると、最終的にはその乱数が事後分布からの乱数になっている(定常分布に収束する)、というわけです。MCMCでは、この推移確率をうまく設定してやることで、事後分布そのものはわからなくても、事後分布からの乱数を得ることができるのです。
ここで問題は、どうやって推移確率を設定するかということになります。この方法にいくつかのタイプがあります。
最初に考案されたのがメトロポリス(・ヘイスティング)法です。次に、ギブスサンプラーというのが提案されます。これは効率はいいんですが、使えるモデルが限られること、複雑なモデルだと自己相関が高くなる(なかなか定常分布に収束しない)という欠点もあります。これらの方法に一貫しているのは、設定をうまくしないと、なかなか密度の高いところのパラメータを多く生成できず、いつまでたっても事後分布の形状に比例した形にならない、という点にあります。事後分布が事前にわからないので仕方ないのですが。
そこで現れたのがHMCです。
以下ちょっと詳しいMCMCの解説。わかってる人、知らなくていい人は次の節まで飛ばしてください。
どういう推移確率を用意すれば、マルコフ連鎖が大局的に事後分布の乱数となるかといえば、、詳細釣り合い条件というのが成り立つことが必要です。詳細釣り合い条件とは、任意の2つのパラメータの値を考えたとき(仮にaとbにしましょう)、次のような関係が成り立つことです。
P(a)T(b|a) = P(b)T(a|b)
ここで、P()は事後分布、T()は推移確率を表していて、T(a|b)はbからaに推移する確率を意味します。つまり、事後分布におけるaの確率密度✕aからbへの推移確率が、事後分布におけるbの確率✕bからaへの推移確率が等しい、ということです。これが任意のaとbに成り立つようなT()を用意すればいいことになります。
事後分布P()はわからんやんけ、という話なんですが、事後分布の計算が難しいのは正規化定数です。これはaでもbでも共通(つまり任意のパラメータの値で共通)なので、aとbの事後分布の比は計算可能です。よってP(a)/P(b) = T(a|b) /T(b|a)となるような推移確率Tを用意すればいいことになるわけです。これは簡単に実現可能、というわけです。
◆ハミルトニアンモンテカルロ法
HMCは物理学のアナロジーを用いて、推移確率を決めます。イメージとしてはこんな感じです。
いま、事後分布の形が正規分布とだとします。実際、事後分布を正確に推定するのは難しいのですが、形状自体は尤度✕事前分布に比例します。たとえば正規分布の平均値パラメータの尤度関数はサンプルサイズが大きいと正規分布に比例した形になり、事前分布に一様分布を仮定すると、事後分布は正規分布になります。
こんな感じ。
この乱数を生成したいとします。
HMCでは事後分布の形状はわかることを利用します。まず、事後分布の対数の符号反転、つまり情報量の関数を考えます。
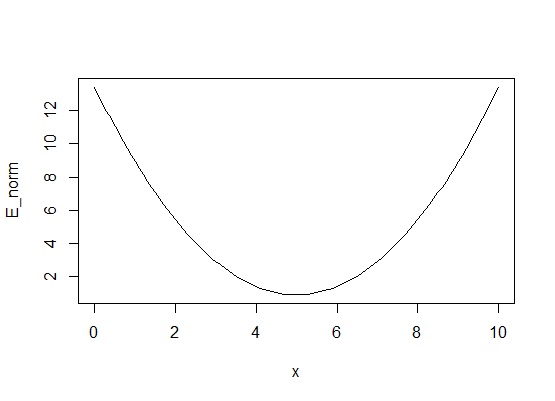
こんなお椀みたいなのになりました。さて、このお椀に玉を適当な場所において転がす事を考えます。そのとき、正規乱数によって転がす強さ(運動量)を決めます。強く弾くと一回遠くまで転がって、また落ちてきて・・・というように幅広い範囲で転がり続けます。弱く弾くと、お椀の下のほうでコロコロ転がってる状態になるでしょう。摩擦がなければ運動量と位置ネルギーの合計(これをハミルトニアンといいます)は一定になるように、ずっと転がり続けます。HMCでは転がす時間を予め決めておいて、その時間になったら玉を止めます。止まったところのX軸の値が、次のパラメータの値とする、という方法です。
そして、その次のパラメータは、前回のパラメータの位置からまた正規乱数によって決めた運動量で弾いて・・・ということを繰り返します。この「ある値から乱数で決めた強さで玉を弾いて、一定時間立って止めた場所が次のパラメータの値」という更新自体が、推移確率になっているということです。
HMCでは、基本的には密度の高いところ(お椀の下の方)に転がることが多くなり、たまーに強く弾くことで事後分布の端のほうもサンプリングできる、そういうアルゴリズムになっています。また、密度の高いところから離れたパラメータが生成された場合、位置エネルギーが大きいため、広い範囲に転がり、密度の高いところにパラメータが生成された場合は、位置エネルギーが小さいため比較的近くを転がりやすくなります。このように、密度が高いところに集中するようになる一方、自己相関が低い乱数を生成することができます。
イメージは上のような感じなんですが、実際には、玉がどこにあるかを判別するために、時間を短い間隔で区切って、離散的に玉の状態を判断します。このとき、微小時間をepsilon、その判定を何回するかをLというハイパーパラメータで決めます。Lとepsilonの積が玉を転がす時間というわけです。これは分析する側が決めなければいけません。
では、まずはRでHMCを実装してみましょう。
◆HMCの実装
まずは今回使うRのパッケージです。
|
1 2 3 |
library(rstan) library(psych) library(magrittr) |
rstanはmonitor関数で使います。magrittrはパイプ演算子を使いたいので。
コードを全部書くと長いので、コアだけ解説します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
HMC <- function(U, q, lower, upper, L, epsilon){ p <- rnorm(length(q),0,1) H_old <- U(q) - sum(p^2)/2 q_old <- q for(l in 1:L){ outLF <- leapfrog(U,epsilon,p,q) p <- outLF$p q <- lower_upper(outLF$q,lower,upper) } H <- U(q) - sum(p^2)/2 if (runif(1) < exp(H-H_old)){ return(q) }else{ return(q_old) } } |
これがHMCのパラメータ更新(乱数生成アルゴリズム)です。どこで乱数があるかといえば、2行目にp(運動量)に対して標準正規乱数が生成されているのがわかると思います。
あとは、予め決めておいたLとepsilonに従って玉の位置を追いかけていきます。玉の位置を把握する関数がleapfrogという関数で、以下です。
|
1 2 3 4 5 6 |
leapfrog <- function(U,epsilon,p,q){ p <- p + epsilon/2 * grad_U(U,q) q <- q + epsilon * p p <- p + epsilon/2 * grad_U(U,q) return(list(p=p,q=q)) } |
pが運動量でqがパラメータの位置を表しています。pとqがちょっとずつ更新されることで、玉の位置が離散的に把握されている感じです。ここで使われているgrad_Uという関数は確率モデルの対数の導関数です。今回の俺式HMCではモデルごとに導関数を計算するのが面倒なのと、一般性を持たせるため、数値微分で計算しています。理想的にはここを自動微分にしてやればもっと計算は早くなります。
これらの関数を使って、mcmc.HMCという関数で実際にMCMCを回していきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
mcmc.HMC <- function(model,init,lower=NULL,upper=NULL,iter=2000,warmup=NULL,chains=4,L=100,epsilon=0.01){ P <- length(init) warmup <- ifelse(is.null(warmup),iter/2,warmup) if(is.null(lower)==TRUE) lower <- rep(-Inf,P) if(is.null(upper)==TRUE) upper <- rep(Inf,P) C <- chains out <- list() for(c in 1:C){ cat("Chain=",c,"\n") par <- matrix(0,iter,length(init)) q <- init for(m in 1:iter){ q <- HMC(U=model,q,lower=lower,upper=upper,L=L,epsilon=epsilon) par[m,] <- q if(m%%500==0) cat("m=",m,", par=",par[m,],"\n") } out[[c]] <- list(par=par) } return(out) } |
では、さっそくこれを使ってMCMCをやってみます。まずは簡単なロジスティック回帰分析をやってみます。
データセットを乱数で作ってみます。切片が-0.5、回帰係数が1.5を真値としました。
|
1 2 3 4 5 6 7 8 9 10 |
##logistic beta <- c(-0.5,1.5) N <- 500 X <- as.matrix(cbind(rep(1,N),seq(-2,2,length.out=N))) mu <- logistic(X%*%beta) Y <- rbinom(N,1,mu) P <- length(beta) lower <- c(rep(-Inf,P)) upper <- c(rep(Inf,P)) init <- c(beta) |
lowerとupperはStanでいうところのlower=と同じで、パラメータの取りうる範囲を指定しています。ロジスティック回帰は分散パラメータがないので推定が楽です。
ロジスティック回帰の確率モデルを対数で書きます。本当は符号反転させるんですが、それはleapfrogの関数で符号を逆にしているので、ここでは何も考えず対数だけとります。
|
1 2 3 4 5 6 7 |
log_logistic <- function(theta){ beta <- theta mu <- logistic(X%*%beta) LL <- sum(dbinom(Y,1,mu,log=TRUE)) LL <- LL + sum(dnorm(beta,0,10^2,log=TRUE)) return(LL) } |
ベルヌーイ分布の対数をLL(log likelihood)に入れて出力します。なお、2つ目のLLを入れている式は、事前分布の対数を入れています。ここでは、回帰係数betaがSD=100の正規分布としています。上は見た目のわかりやすさのためにRの関数で対数確率を直接書いていますが、次のように直接書き下してもいいです。
|
1 2 3 4 5 6 7 8 |
log_logistic <- function(theta){ beta <- theta mu <- logistic(X%*%beta) LL <- sum(Y*log(mu)+(1-Y)*log(1-mu)) scale <- 10^2 LL <- LL -P/2*log(2*pi*scale^2)-sum(beta^2)/(2*scale^2) return(LL) } |
さて、HMCを実行してみます。Lは適当に25回、epsilonは0.01としました。MCMCサンプルは2000回サンプリングをして、半分はバーンインとして捨てます。チェインは2でやってます。
|
1 2 3 4 5 6 7 8 9 |
#mcmc setting iter <- 2000 C <- 2 #HMC source("HMC.R") t<-proc.time() out <- mcmc.HMC(model=log_logistic,init=init,lower=lower,upper=upper,iter=iter,chains=C,L=25,epsilon=0.01) proc.time()-t |
推定は38秒程かかりました。
結果は、次のようにmcmcというオブジェクトに配列で整理して、rstanパッケージのmonitorで見てみます。monitorはサンプル✕チェイン✕パラメータの配列を用意すればOKです。
|
1 2 3 4 5 6 7 8 |
#result mcmc <- array(dim=c(iter,C,length(init))) for(c in 1:C){ for(i in 1:length(init)){ mcmc[,c,i] <- out[[c]]$par[,i] } } mcmc %>% monitor(digits_summary = 2) |
|
1 2 3 4 5 6 |
>mcmc %>% monitor(digits_summary = 2) Inference for the input samples (2 chains: each with iter=2000; warmup=1000): mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat V1 -0.55 0.01 0.19 -0.92 -0.68 -0.54 -0.42 -0.18 1224 1 V2 1.26 0.01 0.18 0.91 1.14 1.26 1.39 1.64 1164 1 |
このように、おおよそ真値に近い値が得られました。Rhatも1に近いです。
traceplotも見てみます。
|
1 2 3 4 5 6 7 8 9 10 |
#trace plot par(mfrow=c(length(init),1)) for(i in 1:length(init)){ temp1 <- mcmc[(iter/2+1):iter,1,i] temp2 <- mcmc[(iter/2+1):iter,2,i] plot(temp1,type="l",ylim=c(min(c(temp1,temp2)),max(c(temp1,temp2))),ylab=paste0("par",i),col="blue") par(new=T) plot(temp2,type="l",ylim=c(min(c(temp1,temp2)),max(c(temp1,temp2))),ylab=paste0("par",i),col="green") } par(mfrow=c(1,1)) |
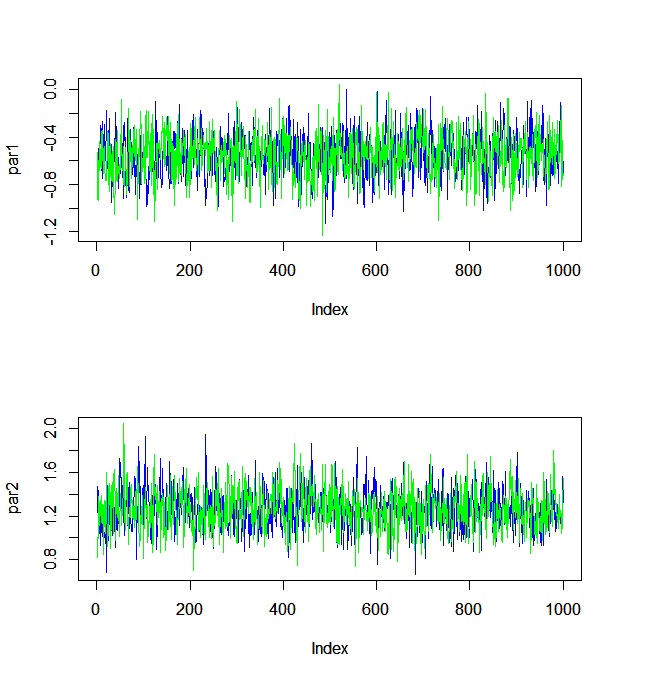
おお、いい感じ。
◆HMCの限界点
さて、HMCの実装がうまくいきました。「これでええやん」と思わないでもないですが、なかなかそうも行かないのです。HMCにはLとepsilonを設定しないといけないのですが、この設定をうまくしないと、さっきみたいにきれいに収束はしてくれません。
試しに今度は正規分布、つまり普通の回帰分析をやってみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
##regression beta <- c(2.0,5.0) sigma <- 0.8 N <- 200 X <- as.matrix(cbind(rep(1,N),seq(-2,2,length.out=N))) Y <- X%*%beta + rnorm(N,0,sigma) P <- length(beta) lower <- c(rep(-Inf,P),0) upper <- c(rep(Inf,P),Inf) init <- c(beta,sigma) log_reg <- function(theta){ P <- length(theta) beta <- theta[1:(P-1)] sigma <-theta[P] mu <- X%*%beta LL <- -N/2*log(2*pi*sigma^2)-sum((Y-mu)^2)/(2*sigma^2) scale <- 10^2 LL <- LL -P/2*log(2*pi*scale^2)-sum(beta^2)/(2*scale^2) scale <- 2.5 LL <- LL -log(pi)+log(scale)-log(sigma^2+scale^2) return(LL) } |
今回は、回帰係数に加えて残差標準偏差σがあるので、それにも事前分布を設定しています。
MCMC(*´Д`)ハァハァ
|
1 2 3 4 5 |
#HMC source("HMC.R") t<-proc.time() out <- mcmc.HMC(model=log_reg,init=init,lower=lower,upper=upper,iter=iter,chains=C,L=25,epsilon=0.01) proc.time()-t |
|
1 2 3 4 5 6 |
Inference for the input samples (2 chains: each with iter=2000; warmup=1000): mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat V1 1.99 0.00 0.06 1.87 1.95 1.99 2.03 2.10 3913 1.00 V2 4.91 0.00 0.05 4.81 4.88 4.92 4.95 5.01 1345 1.00 V3 0.83 0.01 0.04 0.76 0.80 0.83 0.86 0.92 53 1.06 |
むむ。v3,つまりこれはσなんですが、のn_effが悪そうです。rhatも微妙に悪いです。
traceplotを見ると・・・
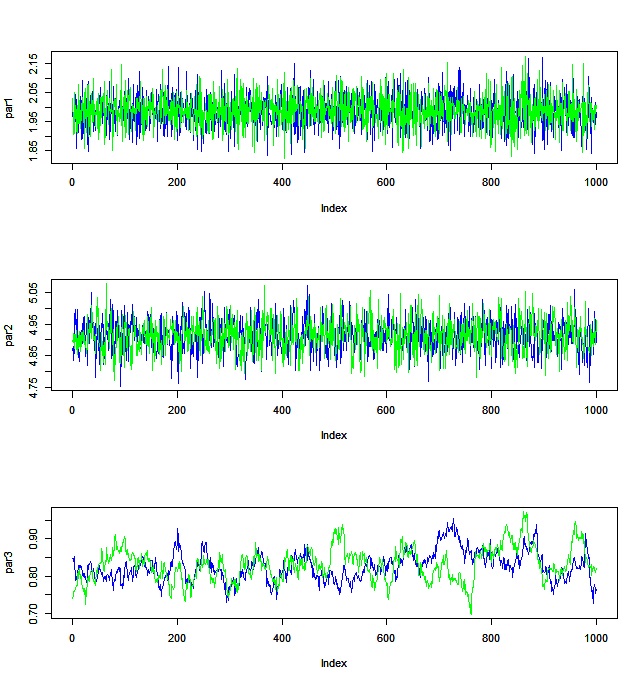
切片や回帰係数はいい感じですが、標準偏差のほうは、自己相関が高くなっているのがわかると思います。
上の例はまだいいほうで、説明変数の相関が高い場合の線形モデルだと、ほぼ使い物にならないぐらいHMCでもうまくいきません。基本的にはLを大きく、epsilonを小さくすれば改善されますが、Lを無駄に大きくすると、玉がずっと同じところを転がり続けて無駄な計算を行うことになります。しかし、どこで止めればいいかはわかりません。epsilonを小さくするとちょっと移動したら止めて、という感じになるので全然玉が動かなくなります。Lが小さい場合は自己相関が大きくなってしまいますので、結局Lを大きくしないといけなくなって、計算量が増えます。Lとepsilonを最適にする必要があります。
◆そこでNUTS
NUTSはNo-U-turn samplerの略で、Uターンしないということですね。これは玉が同じところに戻ってきたら、サンプリングをやめるアルゴリズムです。
NUTSは玉が前と同じ場所に帰ってきたら、それまでに通った軌跡からランダムにパラメータを選びます。本当はもう少しややこしいアルゴリズムなんですが、イメージとしてはそんな感じです。こうすることで、Uターンするまで玉を転がせばいい、という目安が出てくるので無駄な計算が減りますし、なにより分析者がLを決めなくてよくなります。
NUTSは基本的にこれだけですが、Stanにはあと2つほど改良が加えられています。それはepsilonの設定で、最適なepsilonをサンプリングしながらちょっとずつ調整していくという、dual averagingというアルゴリズムを追加します。Stanはバーンインではなくてwarmupという言葉が使われていますが、実はwarmup中にepsilonを最適化してるんです。で、warmupが終わったらその最適化されたepsilonを固定してサンプリングを行います。その意味でも、Stanはwarmupのパラメータは捨てたほうがいいかもです。
もう一つは、HMCではepsilonはすべてのパラメータで同じものが使われるんですが、パラメータの種類によっては変えたほうが効率性が上がります。あるパラメータは雑に更新して、別のパラメータは緻密に更新する、とういことができるようになります。これはパラメータの分散(あるいは共分散も)を利用し、分散が大きいパラメータはepslionが大きくなるようにします。こうすることで、すべてのパラメータがバランスよく効率的にサンプリングできます。
NUTSの詳細はこちらの論文に詳しいのでどうぞ。
というわけで、NUTSをRで実装しました。名付けて、俺式NUTS。NUTS俺式でもいいです(どっちでもいい)。
NUTSのアルゴリズムはいろいろ細かくてややこしいのでコードは最後に回すとして、実際に上のアルゴリズムを実装したものを使ってみましょう。さっきうまく行かなかった回帰分析をやってみます。
NUTSのいい点は、基本的にはハイパーパラメータをいじらなくていい点です。何も考えずにどーんとモデルを入れます。
|
1 2 3 4 5 |
#NUTS source("NUTS.R") t<-proc.time() out <- mcmc.NUTS(model=log_reg,init=init,lower=lower,upper=upper,iter=iter,chains=C) proc.time()-t |
HMCだと回帰分析で11秒かかりましたが、NUTSだと3秒出終わりました。これは最適なLとepsilonが選ばれて、計算回数が少なくなっているからです。
|
1 2 3 4 5 6 |
Inference for the input samples (2 chains: each with iter=2000; warmup=1000): mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat V1 1.99 0 0.06 1.87 1.95 1.99 2.03 2.10 3029 1 V2 4.91 0 0.05 4.81 4.88 4.91 4.95 5.02 2880 1 V3 0.84 0 0.04 0.76 0.80 0.83 0.87 0.93 2300 1 |
結果はこのように、いい感じに収束してそうなのがわかります。
traceplotを見ても・・・
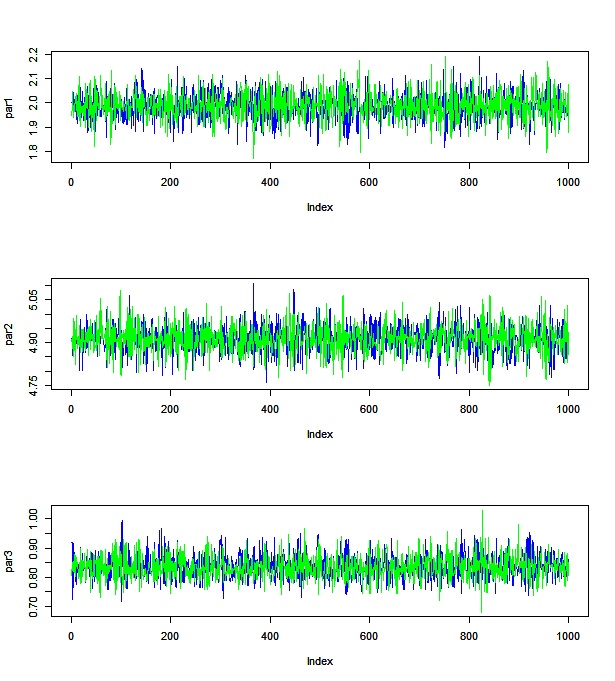
いい感じに自己相関が低そうなのがわかると思います。
さて、NUTSではハイパーパラメータがない、というような感じのことを言いましたが、実際にはあります。deltaというパラメータがそれです(実際には他にもありますが、いじらなくて問題ないです)。
deltaはHMCのステップでの採用率を表しています。HMCではハミルトニアン力学の予測値と一致していない場合、そのパラメータを不一致の程度に合わせて不採用にして、もう一度玉を転がし直します。その採用率をあげるためにはより緻密に計算しないといけないのでepsilonが小さくなります。端的に言えば、よりMCMCが正確になる一方、時間がかかるわけです。
Stanのデフォルトは0.8となっています。もしMCMCがうまくいってなさそうなら、deltaを0.95とかにあげてみてください。
あと、今回は実装してないけどStanでもっと効率的にしているものがいくつかあります。僕も完全に理解しきれてないので説明もうまくできませんが、Stanはすごい、ということです(雑)。
◆俺式NUTSでMCMC
Stanではモデルを自由に書いてパラメータを推定することができます。それは、そもそもMCMCが汎用的なアルゴリズムなのに加えて、NUTS(with dual averaging)ではハイパーパラメータの設定もいらなくなったからです。
HMCでは確率モデルの各パラメータについての導関数が必要です。今回は数値微分を使っていますが、計算効率が良くないので、Stanではそういうことをしておらず、自動微分というアルゴリズムを使っています。自動微分については来週のStanアドカレ記事で紹介します。
自動微分さえできれば、あとは確率モデルを好きに書けばいいのです。僕がRに実装した俺式NUTSでも、ポアソン回帰をしたいなと思えば、次のようにRの関数を利用して簡単にかけます。
|
1 2 3 4 5 6 7 |
log_poisson <- function(theta){ beta <- theta mu <- exp(X%*%beta) LL <- sum(dpois(Y,mu,log=T)) LL <- LL + sum(dnorm(beta,0,10^2),log=T) return(LL) } |
どうでしょう。Stanのtaget +=の記法とほとんど同じような感じで書けますね。
これを次のように推定すると・・・
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
##poisson beta <- c(0.1,0.2) N <- 200 X <- as.matrix(cbind(rep(1,N),seq(0,2,length.out=N))) mu <- exp(X%*%beta) Y <- rpois(N,mu) P <- length(beta) lower <- c(rep(-Inf,P)) upper <- c(rep(Inf,P)) init <- c(beta) #NUTS source("NUTS.R") t<-proc.time() out <- mcmc.NUTS(model=log_poisson,init=init,lower=lower,upper=upper,iter=iter,chains=C) proc.time()-t |
ででーん!
|
1 2 3 4 5 |
Inference for the input samples (2 chains: each with iter=2000; warmup=1000): mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat V1 0.03 0.01 0.13 -0.21 -0.05 0.03 0.12 0.28 514 1 V2 0.27 0.00 0.10 0.08 0.20 0.27 0.35 0.47 490 1 |
となります。
このポアソン回帰をStanで全く同じモデルを書いてNUTSで推定してみます。
Stanコードはこれ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
data{ int N; int P; int Y[N]; matrix[N,P] X; } parameters{ vector[P] beta; } model{ vector[N] mu = exp(X*beta); Y ~ poisson(mu); beta ~ normal(0,10^2); } |
Rコードはこれ。
|
1 2 3 4 5 6 7 8 |
model <- stan_model("poisson.stan") datastan <- list(N=N,P=P,Y=as.vector(Y),X=X) fit <- sampling(model,data=datastan,iter=2000,chains=2,algorithm =c("NUTS"), control=list(adapt_delta=0.8)) fit |
結果はこれ。
|
1 2 3 4 5 6 7 8 9 |
>fit Inference for Stan model: poisson. 2 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 0.05 0.01 0.13 -0.21 -0.04 0.05 0.13 0.28 489 1.01 beta[2] 0.26 0.00 0.10 0.07 0.19 0.26 0.33 0.47 501 1.01 lp__ -184.64 0.03 0.92 -187.12 -185.05 -184.34 -183.98 -183.74 713 1.00 |
n_effも俺式NUTSとほぼ同じような感じになっているのがわかると思います。
ただ、Stanは3秒程度で終わったのに、俺式NUTSは19秒もかかりました。ぐ・・・。
◆俺式NUTSブースト
いろいろ俺式NUTSでやってると、Stanより遅いことが気になります。くやしいです。そもそも数値微分している時点で遅いのは当たり前なんですが、こっちで設定した対数確率モデルの計算がもっと早くなれば、俺式NUTSも早くなるんじゃないでしょうか。
そこで思いついたのが、Stanで確率モデルを書いてやって、それをRの関数として呼び出せばいいんじゃないか、という技です。
「お前は何を言ってるんだ」
とかいわない。
まずStanで次のようなfunctionを作ります。
|
1 2 3 4 5 6 7 8 |
functions{ real log_reg_stan(vector beta, int[] Y, matrix X){ real LL = 0; LL += poisson_log_lpmf(Y|X*beta); LL += normal_lpdf(beta|0,10^2); return(LL); } } |
ほぼほぼtarget記法の書き方と同じですね。
さて、今度はこれをR内部で使えるようにします。rstan::expose_stan_functions()を使ってStanコードをコンパイルし、R関数に変換します。そしてその関数に引数を入れてやれば完成です。
|
1 2 3 4 5 6 7 |
rstan::expose_stan_functions("log_poisson.stan") log_poisson_boost <- function(theta){ beta <- theta LL <- log_reg_stan(beta,Y,X) return(LL) } |
さっきは19秒強かかった俺式NUTSですが、boostを使えば・・・
|
1 2 3 |
proc.time()-t ユーザ システム 経過 10.64 0.00 10.69 |
Yeeeeah! なんと半分の時間で終わりました。
といっても、Stanの3秒には敵いませんでしが・・・。
しかし、この方法だとパラメータの宣言とかいらないし、コードは短くなりますね。そういう長所は・・・ないわけではない。
というわけで長い記事になりましたが、NUTSをStanを使って実装する、というお話でした。
ちゃんちゃん。
◆俺式NUTSのコード
最後に、俺式NUTSのコードをあげておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 |
mcmc.NUTS <- function(model,init,lower=NULL,upper=NULL,iter=2000,warmup=NULL,chains=4,delta=0.8){ P <- length(init) warmup <- ifelse(is.null(warmup),iter/2,warmup) if(is.null(lower)==TRUE) lower <- rep(-Inf,P) if(is.null(upper)==TRUE) upper <- rep(Inf,P) C <- chains out <- list() for(c in 1:C){ cat("Chain=",c,"\n") out[[c]] <- NUTS_DA(U=model,init_epsilon=1,init=init,lower=lower,upper=upper,delta=delta, iter=iter,warmup=warmup) } return(out) } grad_U <- function(U,theta){ p <- length(theta) h <- 0.001 f <- U(theta) dtheta <- c() for(i in 1:p){ theta_h <- theta theta_h[i] <- theta[i]+h dtheta[i] <- (U(theta_h)-f)/h } return(dtheta) } leapfrog <- function(U,epsilon,p,q,M_inv){ epsilon <- epsilon*M_inv p <- p + epsilon/2 * grad_U(U,q) q <- q + epsilon * p p <- p + epsilon/2 * grad_U(U,q) return(list(p=p,q=q)) } lower_upper <- function(theta,lower,upper){ p <- length(theta) for(i in 1:p){ if(theta[i] < lower[i]){ theta[i] <- lower[i] + 0.0001 }else if(theta[i]> upper[i]){ theta[i] <- upper[i] - 0.0011 } } return(theta) } FindReasonableEpsilpon <- function(U,init_epsilon,q,lower,upper){ epsilon <- init_epsilon p <- rnorm(length(q),0,1) H_old <- U(q) - sum(p^2)/2 M_inv <- rep(1,length(q)) outLF <- leapfrog(U,epsilon,p,q,M_inv) outLF$q <- lower_upper(outLF$q,lower,upper) H_new <- U(outLF$q) - sum(outLF$p^2)/2 ratio <- min(1,exp(H_new-H_old)) a <- 2*ifelse(ratio > 0.5,1,0)-1 while(ratio^a > 2^(-a)){ epsilon <- 2^a*epsilon outLF <- leapfrog(U,epsilon,p,q,M_inv) outLF$q <- lower_upper(outLF$q,lower,upper) H_new <- U(outLF$q) - sum(outLF$p^2)/2 ratio <- min(1,exp(H_new-H_old)) } epsilon <- ifelse(epsilon<0.001,0.001,epsilon) return(epsilon) } NUTS_DA <- function(U,init_epsilon, init, lower,upper, delta, iter, warmup){ par <- matrix(0,iter,length(init)) accept <- c() stepsize <- c() treedepth <- c() M_adapt <- warmup epsilon <- FindReasonableEpsilpon(U=U,init_epsilon=init_epsilon,q=init,lower,upper) mu <- log(10*epsilon) Hbar <- 0 gamma <- 0.05 t0 <- 10 kappa <- 0.75 epsilon_bar <- 1 log_epsilon_bar <- log(epsilon_bar) q0 <- init M_inv <- rep(1,length(q0)) k <- 1 #mcmc start for(m in 1:iter){ p0 <- rnorm(length(q0),0,1) H0 <- U(q0) - sum(p0^2)/2 u <- runif(1,0,exp(H0)) q_plus <- q0 q_minus <- q0 p_plus <- p0 p_minus <- p0 j <- 0 q <- q0 n <- 1 s <- 1 while(s==1){ v <- ifelse(runif(1)>0.5,-1,1) if(v==-1){ out <- BuildTree(U,p_minus,q_minus,u,v,j,epsilon,H0,M_inv,lower,upper) p_minus <- out$p_minus q_minus <- out$q_minus }else{ out <- BuildTree(U,p_plus,q_plus,u,v,j,epsilon,H0,M_inv,lower,upper) p_plus <- out$p_plus q_plus <- out$q_plus } q2 <- out$q n2 <- out$n s2 <- out$s alpha <- out$alpha n_alpha <- out$n_alpha if(s2 == 1){ if (runif(1) < n2/n){ q <- q2 } } n <- n + n2 s <- s2*ifelse((q_plus-q_minus)%*%p_minus>=0,1,0)*ifelse((q_plus-q_minus)%*%p_plus>=0,1,0) j <- j+1 } par[m,] <- q q0 <- q #dual averaging if(m < M_adapt){ Hbar <- (1-1/(m+t0))*Hbar + 1/(m+t0)*(delta-(alpha/n_alpha)) log_epsilon <- mu - sqrt(m)/gamma*Hbar log_epsilon_bar <- m^-kappa*log_epsilon + (1-m^-kappa)*log_epsilon_bar epsilon <- exp(log_epsilon) epsilon_bar <- exp(log_epsilon_bar) if(m > (M_adapt-25)){ }else if(m > 75){ if(m%%(50*k)==0){ M_inv <- apply(par[(m-50*k):m,],2,sd) k <- k + 1 } } }else{ epsilon <- epsilon_bar } if(m%%500==0) cat("m=",m,", epsilon=",epsilon,"\n") accept[m] <- alpha/n_alpha stepsize[m] <- epsilon treedepth[m] <- j } return(list(par=par,accept=accept,stepsize=stepsize,treedepth=treedepth,M_inv=M_inv)) } BuildTree <- function(U,p,q,u,v,j,epsilon,H0,M_inv,lower,upper){ if(j==0){ outLF <- leapfrog(U,v*epsilon,p,q,M_inv) p2 <- outLF$p q2 <- lower_upper(outLF$q,lower,upper) H <- U(q2) - sum(p2^2)/2 n2 <- ifelse(u<=exp(H),1,0) s2 <- ifelse(u<=exp(1000+H),1,0) alpha <- min(1,exp(H - H0)) n_alpha <- 1 outBT = list(q_minus=q2,q_plus=q2,p_minus=p2,p_plus=p2,q=q2,n=n2,s=s2,alpha=alpha,n_alpha=n_alpha) }else{ out2 <- BuildTree(U,p,q,u,v,j-1,epsilon,H0,M_inv,lower,upper) p_minus <- out2$p_minus q_minus <- out2$q_minus p_plus <- out2$p_plus q_plus <- out2$q_plus q2 <- out2$q n2 <- out2$n s2 <- out2$s alpha2 <- out2$alpha n_alpha2 <- out2$n_alpha if(s2==1){ if(v==-1){ out3 <- BuildTree(U,p_minus,q_minus,u,v,j-1,epsilon,H0,M_inv,lower,upper) p_minus <- out3$p_minus q_minus <- out3$q_minus }else{ out3<- BuildTree(U,p_plus,q_plus,u,v,j-1,epsilon,H0,M_inv,lower,upper) p_plus <- out3$p_plus q_plus <- out3$q_plus } q3 <- out3$q n3 <- out3$n s3 <- out3$s alpha3 <- out3$alpha n_alpha3 <- out3$n_alpha temp <- ifelse(n3==0,0,n3/(n2+n3)) if(runif(1) < temp){ q2 <- q3 } alpha2 <- alpha2 + alpha3 n_alpha2 <- n_alpha2 + n_alpha3 s2 <- s3*ifelse((q_plus-q_minus)%*%p_minus>=0,1,0)*ifelse((q_plus-q_minus)%*%p_plus>=0,1,0) n2 <- n2 + n3 } outBT = list(q_minus=q_minus,q_plus=q_plus,p_minus=p_minus,p_plus=p_plus,q=q2,n=n2,s=s2,alpha=alpha2,n_alpha=n_alpha2) } } |