この記事では,重回帰分析で交互作用を検討するとはどういうことか,ということを書きます。数学的な話はありません。またより詳しいことを知りたい場合は,前田先生のWebサイトを参照してください。
交互作用効果のおさらい
分散分析では,2要因以上の計画の場合,要因間の交互作用効果を検討することがあります。
交互作用効果とは,要因の効果が,別の要因によって変化することを指します。例えば,次のような例を考えてみましょう。
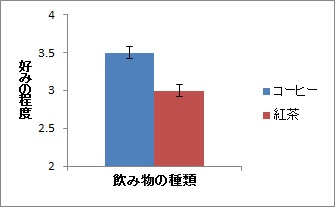
何人かの人にコーヒーと紅茶の好みをそれぞれ尋ねてみたとしましょう。日本だとコーヒーのほうが飲まれている頻度は多いように思うので,(推測ですが)おそらくこんな感じのグラフになるでしょう。
しかし,どちらかというと,コーヒーは男性が好きで,女性は紅茶のほうが好きなのかもしれません。このように,コーヒーと紅茶という飲み物の効果が,男性と女性で異なる,ということを考えるとそれは交互作用を考えていることになります。
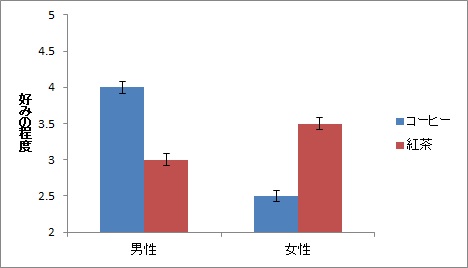
例えば,次のような結果が,交互作用効果が出ている例です。
男性はコーヒーのほうが好きだけど,女性は紅茶のほうが好き,という結果が得られているのがわかります。つまり,飲み物の効果が性別によって違う,というわけです。
最近だと,「恋愛はお金じゃない,ただし,イケメンに限る」なんていう(酷い)言い方がネットでよく言われます。これも交互作用効果の典型例です。
交互作用効果は,場合によっては調整効果(moderation effect)と呼ばれることもあります。上の例では,飲み物の効果が,性別によって調整されている,と表現します。
重回帰分析で交互作用効果
さて,交互作用効果は分散分析で検討するものだと思っている人も多いかもしれません。しかし,最近では重回帰分析でも交互作用効果を検討することが増えてきました。
回帰分析における交互作用効果も,基本的には分散分析の場合と同様の解釈が可能です。つまり,ある変数の回帰係数が,別の変数によって調整される,ということです。
例を考えてみましょう。仮に,「恋愛はお金じゃない,ただしイケメンに限る」というのを主張を回帰分析の交互作用効果で表現してみましょう。
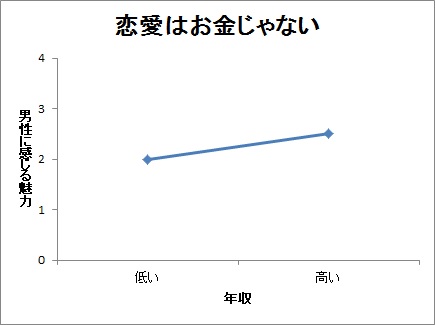
まず,恋愛はお金じゃない,というのが最初の主張ですから,男性への魅力とその男性の年収には無相関が仮定されています。これをグラフで表現すると以下のようになります。
多少効果はありそうですが,それほど年収による魅力の変化は小さそうです。
しかし,この効果は男性の容姿(イケメンの程度)で変わる,と考えるのが交互作用効果の考え方でした。つまり,容姿によって年収の効果は調整されます。
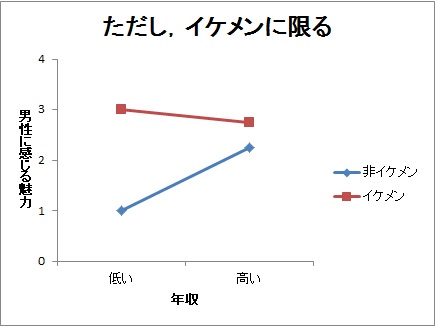
以下のような感じです(※もちろん,あくまで例であって実際のデータではありません)。
ひどい話ですが,非イケメンは年収の効果がありますが,イケメンは年収の効果がありません。つまり,「恋愛はお金じゃない,ただしイケメンだけはそれが当てはまる」ということであり,非イケメンは年収の効果がある,という主張なわけです。
このように,男性の容姿という連続的な変数であっても,重回帰分析で交互作用効果を検討することができます。上の例の場合,容姿がよくなるほど,魅力と年収の効果は小さくなっていく,という連続的な解釈が可能です。
連続的な変数同士の交互作用を分散分析で検討することの問題
さて,上の例の場合,年収とイケメンの程度を,得点の平均値で群分けして,2要因分散分析で検討する,という方法でも同様に検討できそうです。
しかし,最近ではそのような二分化による交互作用の検討は行われていません。なぜなら,せっかく連続的な変数としてデータを取ったのに,わざわざ情報を削って二つに分けるのは全く意味がないからです。
具体的には以下のような問題があります。
- 検定力が低下する:つまり,不当に有意になりにくくなります。
- 誤った解釈を導く:二分化と連続的な交互作用を使い分けることで,恣意的な解釈ができてしまいます。
よって,「連続的なものは,できるだけ連続的に」というのが近年の主流の考え方です。
重回帰分析の交互作用の検討方法
ここでは具体的な方法については書きませんが,先ほど紹介した,前田先生のページに,数学的な話が書いてありますので,そちらを参照してみてください。
また,清水が作ったHADという統計ソフトでも重回帰分析の交互作用の検討が可能です。
HADについてはこちら
また,Rで重回帰分析の交互作用を検討する方法についてはこちらを参照してください。
重回帰分析の交互作用の検討方法はこちら