平均値の差の検定における,等分散性の仮定
知っている人も多いと思いますが,二郡の平均値の差の検定(t検定)を行う時,群ごとの分散が等しいという仮定があります。
2群の分散が等しくない場合,検定結果は正しくなくなります。特に,サンプルサイズが両群で異なる場合,その傾向は顕著になります。このあたりについては,青木先生のサイトのシミュレーションが参考になります。
等分散性が成り立ってない場合,Welchの検定を用いることでただし検定結果を得ることができます。よく用いられる方法に,等分散性の検定を行って,もし等分散が成り立っていれば普通のt検定,成り立っていなければWelch検定という手続きがあります。しかし,これについても青木先生のサイトのシミュレーションが明らかにしているように,Welchの検定は等分散が成り立っていても成り立っていなくても常に正しい結果を出すので,常にWelchの検定を行うべきです。また,等分散の検定→t検定は,検定の二重性の問題があり,有意水準を維持できなくなる問題があります。なので,二群の平均値の差の検定については,常にWelchの検定を利用しましょう。
回帰分析における均一分散の仮定
さて,二群の平均値の差の検定(t検定)についてはWelchの検定でめでたしめでたしなわけですが,同じくt分布を用いる回帰分析の検定はどうでしょうか。実は,回帰分析にも平均値の差の検定と同じく,等分散性の仮定と同じような仮定があります。それは,均一分散(homoscedasticity)の仮定です。
分散の均一性の仮定とは,残差の分散に偏りがないことです。いわば,等分散性の仮定を,連続量に一般化したようなものです。平均値の差の検定と同じく,残差が不均一な分散を持つ場合,回帰分析で計算される標準誤差は正しくなくなります。よって,検定結果も正しくありません。
回帰分析において,不均一分散の問題は心理学ではあまり問題視されてないように見えますが,あまり無視できるものではありません。場合によっては,かなり検定結果にバイアスが生じることがあるので,注意が必要です。
この不均一分散の問題について,Welch検定と同じく,回帰分析にも対応策が用意されています。それは,頑健性のある標準誤差(robust standard error;以下,ロバスト標準誤差)というものです。ロバスト標準誤差とは,残差の均一性の仮定に対して頑健な標準誤差の推定を行います。
特に,ポアソン回帰の場合は,過分散に対してかなり脆弱ですが,それについてもうまく補正してくれます。過分散の対処として負の二項分布による回帰が使われますが,それとも併用してロバスト標準誤差を利用できます。
SPSSでは,一般化線形モデルにはロバスト標準誤差の機能がありますが,通常の回帰分析にはありません。Rにはさまざまな統計分析についてロバスト標準誤差を推定してくれるパッケージがあります(robustbaseなど)。
HADもver10から,一般化線形モデルではデフォルトでロバスト標準誤差を利用できます。また,ver10.41から,回帰分析でもロバスト標準誤差を利用できるようになりました。オプションで「不均一分散の補正」を選ぶと,実行できます。
回帰分析における残差の独立性の仮定
回帰分析には,実は残差の均一性だけではなく,残差の独立性の仮定もあります。残差の独立性とは,データがすべて独立にサンプリングされることで成立します。逆にいえば,たとえばグループ単位でサンプリングされるような階層的なデータでは,残差の独立性の仮定が成立しません。なぜなら,グループ内では,グループ間に比べてデータが類似する傾向があるからです。もし残差の独立性の仮定が満たされない場合,通常の標準誤差では過小評価されてしまいます。
このような,グループ単位でサンプリングされるようなデータには,近年ではマルチレベルモデルが利用されます。マルチレベルモデルでは,グループ単位の類似性をデータの残差と切り分けて推定することで,残差の独立性を担保するわけです。
しかし実は,マルチレベルモデルを使わずとも,グループ内の相関に対しても頑健な標準誤差を用いることで,かなりバイアスを是正することができます。そのようなロバスト標準誤差を,クラスタロバスト標準誤差(clustered robust standard error)と呼びます。クラスタロバスト標準誤差を用いると,本来ならマルチレベルモデルを必要とするような階層的データでも,検定自体は適切に行うことができます。
ではマルチレベルモデルが必要ないかといえば,そうではありません。マルチレベルモデルは,切片や回帰係数のグループ間変動そのものを推定できるので,より細やかなモデリングが可能です。とくに,目的変数が連続変量かつ正規性が満たされたデータなら,HLMなどの方法はかなり手軽に利用できるようになっているので,積極的にHLMなどを利用するといいでしょう。
ただ,目的変数にロジットリンクを仮定したり,ログリンクのポアソン分布を仮定したりする場合,切片や回帰係数のグループ間変動を推定するのは容易ではありません。それは,仮定する分布が二項分布+正規分布,あるいはポアソン+正規分布といったように,異なる分布を同時に推定する必要があるからです。
一般化線形混合モデルは,こういった複雑な推定を行いますが,複雑なだけあって,推定アルゴリズムによって推定結果が違ったりするなど,なかなか難しい問題もあります。SPSSやSASでは疑似尤度を用いた方法を使いますが,尤度を計算できないので,AICなどの情報量規準が利用できないなどの問題があります。
そういったときに,クラスタロバスト標準誤差の利用は可能性が出てきます。最尤法で簡単に計算できるので推定は安定し,しかも妥当な検定を可能にしてくれます。また,マルチレベルモデルになじみのない人でも,標準誤差を補正しているだけなので,使いやすい点も利点かもしれません。
【追記】ただ,統計モデリングの観点から言えば,標準誤差だけを補正する,というのはあまりよい方法であるとはいえないでしょう。モデルの仮定が満たされない場合は,より仮定をゆるめるようなモデリングをするほうがよいと思われます。
HADではver10から一般化線形モデルでクラスタロバスト標準誤差を利用できます。また,ver10.41から普通の回帰分析でもクラスタロバスト標準誤差を利用できるようになりました。回帰分析のオプションから,「クラスタ内相関の補正」を選択すると,利用できます。
HADによるHLMと回帰分析の比較
それでは,HADを使って,HLMとクラスタロバスト標準誤差を使った回帰分析の結果を比較してみましょう。
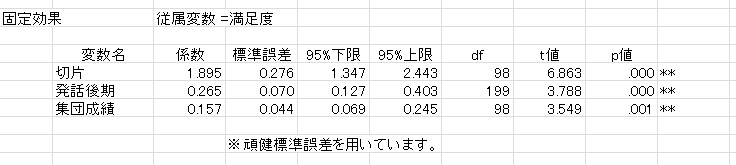
まず,HLMの結果。ここでは,HLMも不均一分散の補正するロバスト標準誤差を使っています。
次に,普通の回帰分析の結果
HLMに比べて,かなり標準誤差が異なっていることがわかります。これは,不均一分散も,グループ内の相関も補正していないからです。
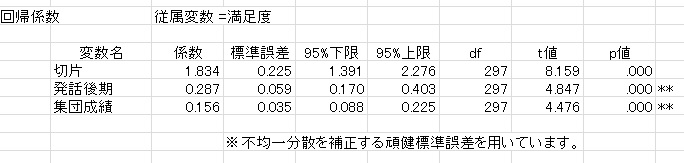
次に,不均一分散を補正した回帰分析の結果です。ただし,グループ内相関は補正していません。
HLMに比べて,やはりかなり小さくなっています。つまり,第一種の過誤が生じている,ということです。また,係数は普通の回帰分析と変わっていません。
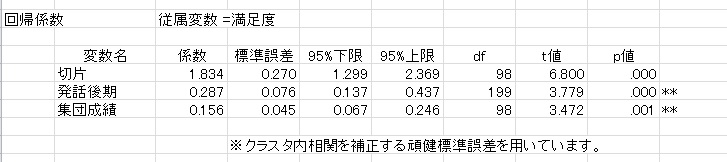
そして,クラスタロバスト標準誤差を用いた回帰分析の結果です。
回帰係数は変わりませんが,標準誤差は,HLMにかなり近くなりました。t値もHLMのものとほぼ同じです。このことから,階層的なデータでも,クラスタロバスト標準誤差を使うことで,誤った検定結果を避けることができることがわかると思います。
自由度の補正
ロバスト標準誤差は便利ですが,漸近理論に基づいているため,大きなサンプルサイズを仮定しています。小サンプルでも正しい検定をするためには,自由度の補正が必要となります。
Welch検定でも,Satterthwaiteの補正自由度を用いて検定しますが,回帰分析でも同様の補正が可能です。ただ,あまりその方法をわかりやすく書いている文献がないため,HADにはまだ未実装です。
ただ,回帰分析を使う場合は極端にサンプルサイズが小さいことは稀な気もするので,そんなに問題はないかなとは思います。サンプルサイズが50以上あれば,それほど外れた検定結果にはならないはずです。
以上のように,心理学の分野ではあまり知られてないですが,回帰分析にも残差の均一分散と独立性の仮定があります。そして,回帰分析はこの家庭からの逸脱に対して脆弱なので,サンプルサイズが大きくても,検定結果を誤ることがあります。それらの仮定の逸脱に対しては,ロバスト標準誤差が有効です。

Pingback: HAD11.30をアップしました。 | Sunny side up!
Pingback: 分析のいろんな仮定と,それに対する頑健さ | Sunny side up!