HAD10.3以降,分散分析の多重比較にd族の効果量を表示するようにしました(以前は相関係数だけ表示していた)。今回の記事では,d族の効果量の計算方法について触れます。
平均値の差の検定(t検定)の効果量
d族の効果量とは,Cohenのdをはじめ,2群の平均値の差を標準化した効果量のことです。
2群の平均値の差の検定(いわゆるt検定)を行うとき,点数の差は当然ながらデータ得点の単位や分散によって変わってきます。しかし,データを標準化するなどして単位をそろえておけば,得られた差は比較可能なものになります。そのような標準化された差のことを,d族の効果量と呼びます。
Cohenが提案したdは,記述統計学的な意味で計算された効果量で,母集団の性質を推測する,推測統計学的な効果量ではありません。そこで,Hedgesは推測統計学的な意味で計算された標準化された差,gを提案しました。ただ,多くの論文では,gをdと表記して記載していることがほとんどです。ただ,記述統計的な効果量であるCohenのdを論文で報告する意味はあまりないので,ここではHedgesのgについて解説します。
Hedgesのgは,
平均値の差 / プールされた標準偏差
という式で計算できます。この手続きは,標準得点を計算するときと同じように,得点を標準偏差で割ることで,差を標準化できることを意味しています。「プールされた」というのは,ここでは2群のデータを1つのデータにまとめた,という程度で理解しておけばいいと思います。
プールされた標準偏差は,以下のように計算します。もともと,推測統計学的な分散や標準偏差(いわゆる,不偏分散,不偏標準偏差)は(n-1)で割りますね。なので,データの標準偏差を一度(n-1)でかけて偏差平方和に戻し,両方の群の偏差平方和の和を,2群分の(n-1)の和で割ります。ここで,群1のサンプルサイズをn1,群2のサンプルサイズをn2,標準偏差をそれぞれSD1,SD2とすると,
というふうに計算できます。式の前半が,n-1をかけて偏差平方和に戻したもの,後半は,もう一度2群の(n-1)の和で割る,という意味です。また,SDはそれぞれ2乗になっている点(つまり分散)に注意してください。
さて,今まで2群の平均値の差の検定,つまり対応のない独立の検定の話でした。では対応のある場合はどうかと言えば,実は上と同じ式で計算できます。つまり,2群というのは対応ある場合だと2変数になりますが,同じようにプールされた標準偏差を計算して,効果量を計算できます。
なお,t値からgを計算する方法もありますが,これは対応のないt検定の場合しか使えないので注意が必要です。t値から計算する方法は,以下の通りです。
分散分析の各平均の差の効果量
一元配置分散分析の場合,プールされた標準偏差の計算は簡単です。
プールされた標準偏差は,分散分析の誤差平均平方の平方根,つまり,
で計算することができます。それを平均値の差から割れば,効果量gが得られます。
あるいは,各推定平均の標準誤差からも計算できます。標準誤差から標準偏差を計算して,そこからプールされた標準偏差を計算すればいいわけです。つまり,各群の標準偏差は
で求めることができます。ここで,添え字のiは,各水準を意味しています。各水準の標準偏差が計算できたら,上と同じ式でプールされた標準偏差を計算すればOKです。
3水準の場合も,比較する群の標準誤差から計算するか,誤差の平均平方の平方根を使うことで効果量を計算できます。ただし,t値を用いた方法は,3水準以上の場合は使えないので注意が必要です。
次に,参加者内要因の場合ですが,誤差の平均平方をそのまま使うことはできません。それに加え,参加者効果の平均平方も使います。以下の式によって,プールされた標準偏差を計算します。
ここで,添え字のsは参加者効果,s*Aは要因の誤差項を意味しています。つまり,それぞれの平均平方に自由度をかけた平方和同士の和を,両方の自由度を合わせたもので割ったものを使うわけです。このようにしないと,参加者間の効果量と比較することができません。
2要因以上の場合
2要因以上の場合でも,すべてが参加者間要因であれば,1元配置分散分析と同じような方法で計算ができ,誤差項の平均平方の平方根でもいいですし,標準誤差から計算しても問題ないです。
次に,すべてが参加者内要因の場合は,上で説明したように当該の要因の誤差項と参加者効果を合わせた平方和から計算した平均平方の平方根を使ってプールされた標準偏差を計算すれば,効果量を算出できます。このとき,ほかの参加者要因の誤差項は含める必要はありません。また,この結果は,標準誤差から標準偏差に戻して計算したものと一致します。
ただ,混合計画の場合は話が別です。混合計画の場合,参加者間要因と参加者内要因では誤差項が異なります。本来のgの定義からすれば,各群の標準偏差からプールされた標準偏差を計算すればいいわけですから,参加者間要因の誤差項だけを用いてプールされた標準偏差を計算すればいいことになります。しかし,これだと参加者内要因の効果量と比較することができなくなります。なぜなら,参加者内要因の場合は参加者効果と自分の誤差項の両方を含めますが,参加者間効果は参加者効果しか計算に使わないからです。
よって,d族のもともとの定義からすると,比較可能なのは混合計画以外,ということになります。
よく考えたら,混合計画でも比較可能な気がしてきました。また調べてから追記します。
【追記 2013/10/24
混合計画でも,1要因分散分析と同じように比較可能な効果量が計算できそうです。ただ,このあたりのちゃんとした文献がないので本当にあっているかはわかりませんが,数値上は一致します。以下のように計算します。
ただし,当該の要因が参加者間要因の場合,分子の部分は参加者効果の平方和だけでOKです。このように計算すると,混合計画でもこれまでと同じ定義の効果量を計算できます。
追記終わり】
しかし,また,一般化効果量の考え方を導入すれば,部分的には解決します。一般化効果量の話は別の記事に譲りますが,すべての誤差項をプールされた標準偏差の計算に用いれば,参加者間でも内でも比較可能なd族の効果量を計算することができます。
そういったものが統計学のほうで提案されているかどうかはわかりません。このあたりはまた調べてから書きます。
共変量がある場合
共変量がある場合でも,上と同じように効果量を計算できます。ただ,共変量の効果を誤差とするかしないか,というのは文献によって異なります。共変量の効果を取り除いた誤差項を用いるなら上記と同じようにできますが,共変量の効果も誤差とするなら,共変量の平方和も誤差項に加えて効果量を計算する必要があります。
一般化効果量の観点から言えば,共変量は個人差を測定した測定要因に含まれますので,共変量は誤差項に含めることになります。
以上が,t検定および分散分析における効果量の求め方です。
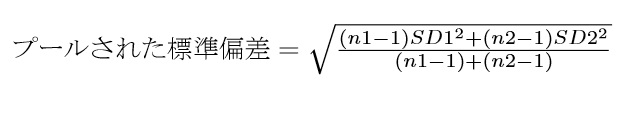
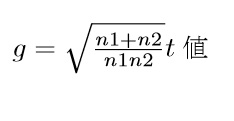


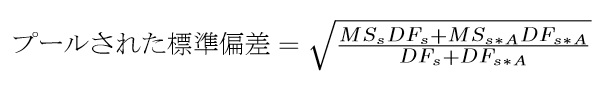

Pingback: 無料で効果量が推定できるソフト – 京極真の研究室